Для подготовки к экзамену по математике
1. Число точек разрыва функции 
равно…
1) 2
2) 1
3) 3
4) 0
2. Функция 
возрастает на интервале(ах)
1) (-2,0)
2) (-2,0) и (0,+ 
)
3) (- ,-2) и (0,+ )
4) (- ,-2) и (-2,0)
3. Пусть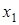 
и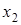 
- точки экстремума функции 
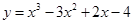, то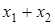 
равно ###
4. Пусть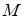 
- наибольшее, а 
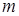- наименьшее значение функции 
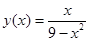на отрезке [-2,2], тогда 
равно ###
5. Пусть 
, тогда абсцисса точки перегиба графика этой функции равна ###
6. Продолжите формулу (С – произвольная постоянная):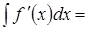 
1) 
2) 
3) 
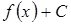
4) 
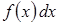
6.1.Укажите все верные утверждения (С – произвольная постоянная)
1) 
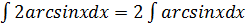
2) 
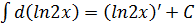
3) 
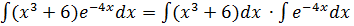
4) 
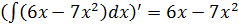
7. Множество всех первообразных функции 
имеет вид
1) 
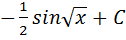
2) 
3) 
4) 
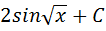
8. Укажите соответствие между функциями и их неопределенными интегралами
| 
|
| 
|
| 
|
| 
|
| 
|
|
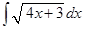
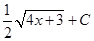
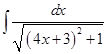
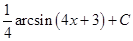
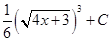
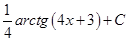
9. В неопределенном интеграле 
введена новая переменная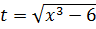 
. Тогда интеграл примет вид:
1) 
2) 
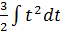
3) 
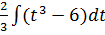
4) 
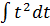
10. Множество первообразных функции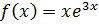 
равно
1) 
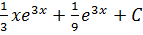
2) 
3) 
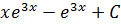
4) 
10.1.Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: 
, положить, что 
, то дифференциал функции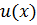 
будет равен
1) 
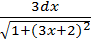
2) 
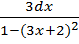
3) 
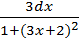
4) 
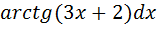
11. В неопределенном интеграле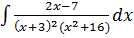 
подынтегральная функция разлагается на элементарные дроби
1) 
2) 
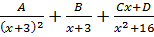
3) 
4) 
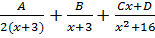
12. В неопределенном интеграле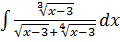 
следует применить подстановку
1) 
2) 
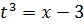
3) 
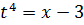
4) 
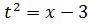
13. В определенном интеграле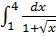 
введена новая переменная 
. Тогда интеграл примет вид:
1) 
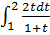
2) 
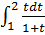
3) 
4) 
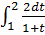
14. Определенный интеграл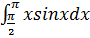 
равен
1) 
2) 
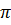
3) 
4) -1
15. Площадь фигуры, ограниченной линиями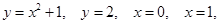 
определяется интегралом
1) 
2) 
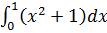
3) 
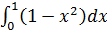
4) 
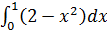
16. Площадь фигуры, ограниченной линиями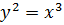 
, 
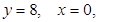
равна ###
17. Несобственными являются следующие интегралы
1) 
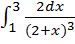
2) 
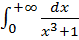
3) 
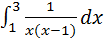
4) 
18. Вычислить несобственный интеграл или установить его расходимость 
1) 
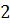
2) 
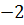
3) 
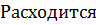
4)
19. Частная производная z´х функции z=ƒ(x;у) определяется как:
1) z´х = 
2) z´х = 
3) z´х = 
.
4) z´х = 
20. Для функции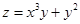 
справедливы соотношения
1) 
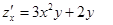
2) 
3) 
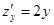
4) 
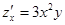
21. Для значений частных производных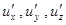 
функции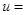 
в точке М (0,-1,1) справедливы утверждения
1) их сумма равна 1;
2) их произведение равно 0;
3) их сумма равна 0;
4) их сумма равна 2;
5) их произведение равно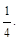 
22. Для функции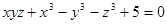 
справедливы соотношения
1) 
2) 
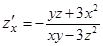
3) 
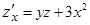
4) 
5) 
23. Для стационарных точек функции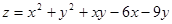 
справедливы утверждения
1) их число равно 1;
2) их число равно 2;
3) сумма их координат равна 2;
4) сумма их координат равна 5.
24. На замкнутой области, ограниченной линиями у = -1, у = 2, х = 0, х = 2, функция 
имеет две стационарные точки М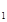 
(0,0) и М 
(1,1). При этом её наименьшее значение в указанной области равно
1) 3
2) -3
3) 0
4) -1
25. Градиентом функции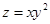 
в точке Р (1,1) является
1) вектор {1,2}
2) вектор {2,1}
3) число 3
4) число 
26. Производной функции 
в точке М (1,1,1) в направлении вектора 
= {1,-1,1} является
1) вектор {2,-2,2}
2) число 
3) вектор {2,2,2}
4) число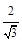 
27. Двойной интеграл 
где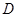 
область ограниченная линиями 
, 
, 
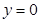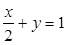равен
1) 
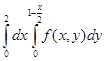
2) 
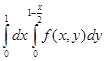
3) 
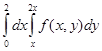
4) 
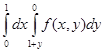
Список вопросов для подготовки к экзамену:
1. Исследование функций одной переменной методами дифференциального исчисления. Экстремум функции. Необходимые и достаточные условия существования экстремума.
2. Выпуклость (вогнутость) функции на интервале. Необходимые и достаточные условия выпуклости (вогнутости) функции.
3. Асимптоты функции. Общая схема исследования функции и построения ее графика.
4. Функция нескольких переменных. Определение, примеры, способы задания.
5. Производная по направлению. Частные производные функции двух переменных. Определение и геометрический смысл.
6. Производные высших порядков. Теорема о смешанных производных
7. Частные дифференциалы и полный дифференциал функции двух переменных.
8. Связь между частными производными и производной по направлению.
9. Градиент функции. Связь с производной по направлению.
10. Производная сложной и неявной функций.
11. Экстремумы функций двух переменных. Необходимые условия. Достаточные условия.
12. Наибольшее и наименьшее значения функции в замкнутой области
13. Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла.
14. Таблица интегралов.
15. Методы интегрирования: непосредственное интегрирование. Метод подстановки. Интегрирование по частям.
16. Определение определенного интеграла.
17. Геометрический смысл определенного интеграла.
18. Свойства определенного интеграла.
19. Формула Ньютона-Лейбница.
20. Метод интегрирования по частям в определенном интеграле. Замена переменной в определенном интеграле.
21. Приложения определенных интегралов: вычисление площадей плоских фигур; объемов пространственных тел; длины дуги кривой.
22. Несобственные интегралы на бесконечном промежутке и от разрывных функций. Геометрический смысл. Теоремы сравнения.
23. Определение кратных интегралов. Теорема существования. Свойства. Вычисление двойного интеграла в декартовых координатах.