Занятие 2. Классическая вероятностная схема.
Основным понятием теории вероятностей является понятие вероятностного пространства.
Вероятностной моделью или вероятностным пространством называют совокупность трех объектов 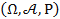 .
.
1.  - представляет собой множество (пространство) элементарных событий или исходов опыта, обозначаемых
- представляет собой множество (пространство) элементарных событий или исходов опыта, обозначаемых  .
.
Примеры 1.
1) При однократном подбрасывании игральной кости элементарным исходом считают выпадение на верхней грани определенного числа очков.
2) При работе датчика случайных чисел элементарный исход – это выпавшее число.
3) Контролер готовой продукции измеряет некоторое количество параметров изделия, при этом результат измерения (совокупность нескольких чисел) также можно считать элементарным исходом.
2. 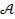 – совокупность подмножеств множества
– совокупность подмножеств множества  , которые называют событиями и обозначают большими латинскими буквами.
, которые называют событиями и обозначают большими латинскими буквами.
Таким образом, события – это множества, и с ними можно производить обычные действия такие, как пересечение, объединение, дополнение и другие. Это накладывает на совокупность подмножеств 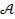 естественные ограничения, которые превращают его в объект, называемый
естественные ограничения, которые превращают его в объект, называемый  – алгеброй.
– алгеброй.
Приведем эти ограничения:
1)  ,
, 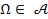
Пустое множество  , или невозможное событие, должно содержаться в
, или невозможное событие, должно содержаться в 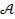 ,
,
все множество  , или достоверное событие, также должно содержаться в
, или достоверное событие, также должно содержаться в 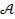 .
.
2) 
То есть наряду с  его дополнение
его дополнение  , или противоположное событие, также должно быть элементом
, или противоположное событие, также должно быть элементом 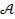 .
.
3) Если  , то
, то 
Пересечение конечного или счетного числа множеств  , или произведение событий
, или произведение событий 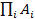 , а также их объединение
, а также их объединение  , или сумма событий
, или сумма событий 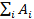 , должны считаться событиями, то есть быть элементами
, должны считаться событиями, то есть быть элементами 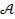 .
.
Определим разность событий  как разность соответствующих множеств
как разность соответствующих множеств  . Согласно свойствам 2) и 3) разность событий является событием.
. Согласно свойствам 2) и 3) разность событий является событием.
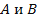 называются несовместными событиями, если
называются несовместными событиями, если 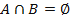 .
.
Говорят также, что событие  влечет событие
влечет событие  (наступление события
(наступление события  влечет наступление события
влечет наступление события 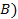 , если
, если  .
.
Если 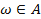 , то говорят, что элементарный исход
, то говорят, что элементарный исход  благоприятен событию
благоприятен событию  .
.
3.  - функция множеств, определенная на
- функция множеств, определенная на 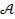 , то есть ставящая в соответствие каждому элементу
, то есть ставящая в соответствие каждому элементу  действительное число
действительное число  , заключенное между 0 и 1 и называемое вероятностью события
, заключенное между 0 и 1 и называемое вероятностью события  . Эта функция должна удовлетворять аксиомам Колмогорова.
. Эта функция должна удовлетворять аксиомам Колмогорова.
1) 
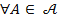 – аксиома неотрицательности вероятности,
– аксиома неотрицательности вероятности,
2) 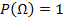 - аксиома нормировки,
- аксиома нормировки,
3)  ), если события
), если события 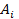 попарно несовместны, то есть
попарно несовместны, то есть  , - аксиома
, - аксиома  - аддитивности.
- аддитивности.
Из аксиом легко устанавливаются следующие свойства вероятности:
1) Если  , то
, то  .
.
Доказательство. Множество  представимо в виде объединения двух непересекающихся множеств
представимо в виде объединения двух непересекающихся множеств  и
и  (событие
(событие  есть сумма двух несовместных событий
есть сумма двух несовместных событий  и
и  ). Тогда по третьей аксиоме
). Тогда по третьей аксиоме 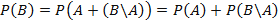 . Откуда
. Откуда

|

|
 .
. 
2) Свойство монотонности.
Если  , то
, то  .
.
Доказательство следует из первого свойства  и первой аксиомы
и первой аксиомы  .
. 
3)  .
.
Доказательство. Левое неравенство – это первая аксиома, а правое следует из того, что  и второй аксиомы.
и второй аксиомы. 
4) 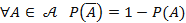 .
.
| B\AB |
| A |
 и
и 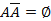 , то по второй и третьей аксиомам
, то по второй и третьей аксиомам  . Откуда
. Откуда  . Свойство установлено.
. Свойство установлено. 
5) Теорема сложения. 
 .
.
Доказательство. Как видно из рисунка, событие  представимо в виде суммы несовместных событий
представимо в виде суммы несовместных событий  и A. По третьей аксиоме
и A. По третьей аксиоме  . А поскольку
. А поскольку  , то по первому свойству
, то по первому свойству  . Комбинация этих двух равенств дает утверждение теоремы.
. Комбинация этих двух равенств дает утверждение теоремы. 
6) Свойство непрерывности. (можно пропустить при первом изложении)
Если  так, что
так, что 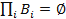 , то
, то  .
.

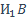
|
 . Тогда
. Тогда  и
и 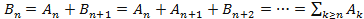 . Тогда по третьей аксиоме
. Тогда по третьей аксиоме 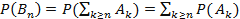 . В частности
. В частности  , что означает сходимость ряда
, что означает сходимость ряда  . Но тогда предел остатка ряда равен нулю
. Но тогда предел остатка ряда равен нулю  .
. 
Пример 2. Определите вероятность того, что партия из 100 изделий, среди которых пять бракованных, будет принята при испытаниях случайным образом выбранных 50 изделий из партии, если условиями приема допускается не более одного бракованного изделия из 50.
Решение. Введем следующие события: 
 .
.
Тогда вероятность того, что партия будет принята, равна 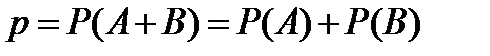 , поскольку события
, поскольку события 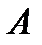 и
и  несовместны.
несовместны.
Вычислим  . Из 100 изделий выбираем 50 -
. Из 100 изделий выбираем 50 -  способов. Из 95 стандартных изделий 50 можно выбрать
способов. Из 95 стандартных изделий 50 можно выбрать  способами. Откуда
способами. Откуда  . Далее, из 5 бракованных выбираем одно -
. Далее, из 5 бракованных выбираем одно -  способов, из 95 стандартных 49 изделий -
способов, из 95 стандартных 49 изделий -  способов. Всего исходов, благоприятствующих
способов. Всего исходов, благоприятствующих  , по правилу произведения существует
, по правилу произведения существует  . Откуда
. Откуда  . Следовательно,
. Следовательно, 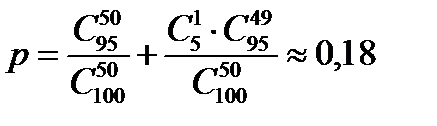 .
.
Пример 3. (задача де Мере) Сколько раз нужно подбросить пару игральных костей, чтобы с вероятностью, большей  , хотя бы один раз выпала пара шестерок?
, хотя бы один раз выпала пара шестерок?
Решение. Если считать, что выпадение пары шестерок – это успех, то  ,
, 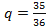 . Пусть событие
. Пусть событие  состоит в том, что хотя бы раз выпала пара шестерок, тогда
состоит в том, что хотя бы раз выпала пара шестерок, тогда  состоит в том, что пара шестерок не выпала ни разу. То есть
состоит в том, что пара шестерок не выпала ни разу. То есть  , а
, а  . Остается разрешить относительно
. Остается разрешить относительно 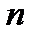 неравенство:
неравенство:  . Получаем:
. Получаем:  ,
,  ,
, 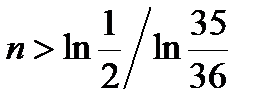 . Численно
. Численно  .
.
Пример 4. (Задача Ньютона) Игрок  бросает 6 игральных костей и выигрывает, если выпадет хотя бы одна шестерка. Игрок
бросает 6 игральных костей и выигрывает, если выпадет хотя бы одна шестерка. Игрок  бросает 12 игральных костей и выигрывает, если выпадет хотя бы две шестерки. У кого больше вероятность выиграть?
бросает 12 игральных костей и выигрывает, если выпадет хотя бы две шестерки. У кого больше вероятность выиграть?
Решение. 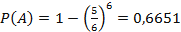

Пример 5. В урне содержится 5 белых и 7 черных шаров. Наугад последовательно выбираются три шара. Найти вероятность того, что черных шаров в выборке будет больше, чем белых.
Решение. Элементарные исходы этого опыта – это всевозможные наборы из трех шаров. Всего таких наборов 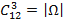 .
.
Пусть событие  . Его можно представить в виде суммы двух несовместных событий
. Его можно представить в виде суммы двух несовместных событий 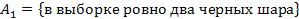 и
и  .
.
Тогда 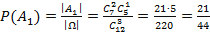 , поскольку благоприятными для события
, поскольку благоприятными для события  будут наборы из двух черных и одного белого шаров, то есть по правилам комбинаторики
будут наборы из двух черных и одного белого шаров, то есть по правилам комбинаторики  . Аналогично
. Аналогично  .
.
Откуда 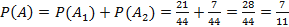 .
.
Пример 6. (для продвинутых) В ящике находится 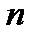 пар перчаток. Из них наугад выбирается
пар перчаток. Из них наугад выбирается  перчаток
перчаток 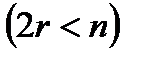 . Какова вероятность, что среди выбранных перчаток отсутствуют парные? Ответ:
. Какова вероятность, что среди выбранных перчаток отсутствуют парные? Ответ: 