Практическое занятие
Тема: Определение размеров поперечного сечения консольной балки
Цель занятия: Приобрести практические навыки и умения в определении размера поперечного сечения консольной балки, нагруженной сосредоточенной силой и сосредоточенным моментом.
Основные теоретические положения:
Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости, проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Брус, работающий при изгибе, называется балкой.
Изгиб называетсяплоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.4).
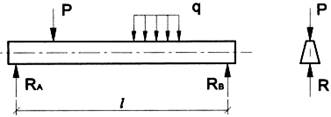
| Рисунок 4 – Схема нагружения при плоском прямом изгибе |
При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M.
Если изгибающий момент 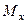 является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы
является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы 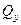 изгиб называется поперечным. К простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
изгиб называется поперечным. К простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
Косой изгиб – изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Сложный изгиб – изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях.
|
|
Осваивать расчет балок удобно, рассматривая по очереди следующие вопросы:
– Определение внутренних усилий в балках и построение эпюр внутренних усилий.
– Проверка прочности балок.
Изгибающий момент М z в любом сечении бруса численно равен алгебраической сумме моментов внешних сил и пар сил, действующих на отсеченную часть, относительно центра тяжести сечения: Миз г = 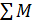 .
.
Поперечная сила считается положительной, если внешние силы поворачивают отсеченную часть балки, относительно рассматриваемого сечения, по ходу часовой стрелки, и отрицательной, если внешние силы поворачивают отсеченную часть балки, относительно рассматриваемого сечения, против хода часовой стрелки. Изгибающий момент считается положительным, если внешние моменты и силы, мысленно закрепленные в рассматриваемом сечении, отсеченную часть бруса изгибают выпуклостью вниз, и отрицательным, если внешние моменты и силы, мысленно закрепленные в рассматриваемом сечении, отсеченную часть бруса изгибают выпуклостью вверх.
Характерными являются те сечения балки, где приложены сосредоточенные силы и моменты, а также сечения, ограничивающие участки с равномерно распределенной нагрузкой. Для построения эпюр Qy и Мизг необходимо использовать правила построения эпюр. Для подбора сечения балки из условия прочности определяют необходимое значение осевого момента сопротивления:
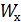
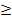
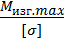 , (6)
, (6)
где 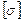 – допускаемое напряжение.
– допускаемое напряжение.
Задание для выполнения работы:
Для стальной консольной балки построить эпюры поперечных сил и изгибающих моментов; подобрать из условия прочности необходимый размер для четных вариантов двутавра, для нечетных вариантов швеллера, приняв [  ]=160 МПа.
]=160 МПа.
|
|
Данные своего варианта взять из таблицы исходных данных.
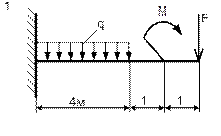
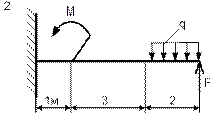
| 
|
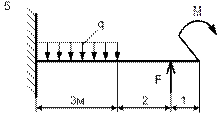
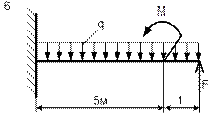
| Схема 1 | Схема 2 |
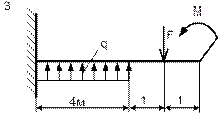
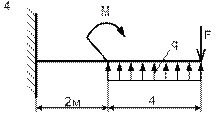
| 
|
| Схема 3 | Схема 4 |
| 
|
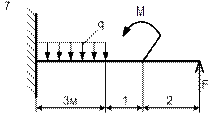
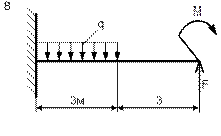
| Схема 5 | Схема 6 |
| 
|
| Схема 7 | Схема 8 |
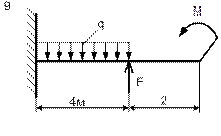
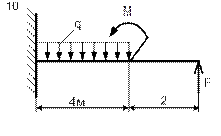
| 
|
| Схема 9 | Схема 10 |
Таблица
Исходные данные к заданию
| Дано | варианты | |||||||||
| схема | ||||||||||
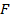 , кН , кН
| ||||||||||
𝑀, кН 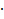 м м
| ||||||||||
| 𝑞, кН/м | ||||||||||
| Дано | варианты | |||||||||
| схема | ||||||||||
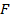 , кН , кН
| ||||||||||
𝑀, кН 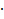 м м
| ||||||||||
| 𝑞, кН/м | ||||||||||
| Дано | варианты | |||||||||
| схема | ||||||||||
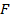 , кН , кН
| ||||||||||
𝑀, кН 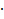 м м
| ||||||||||
| 𝑞, кН/м |
Перечень вопросов, выносимых на обсуждение:
Внутренние силовые факторы при изгибе. Эпюры поперечных сил и изгибающих моментов. Напряжение при изгибе. Расчеты на прочность при изгибе. Линейные и угловые перемещения при изгибе, их определение. Расчеты на жесткость.
Средства обучения/Перечень оборудования, используемого при выполнении работы:
|
|
Опорный конспект, нормативная, справочная и рекомендованная учебно-методическая литература / Бумага стандартного формата А4, карандаш, ручка, линейка, калькулятор.
Рекомендации по выполнению работы:
Для выполнения работы рекомендуется следующая последовательность действий:
1) выполнить расчетную схему, указав на ней все размеры и нагрузки;
2) найти опорные реакции балки (для консоли их можно не находить);
3) балку разделить на участки, границами которых являются сечения, в которых приложены: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается равномерно распределенная нагрузка;
4) выбрать расположение координатных осей, совместив ось z с осью балки, а оси у и х расположить в плоскости сечения (обычно ось у расположена вертикально);
5) применяя метод сечений, вычислить значения поперечных сил в характерных сечениях и построить эпюру поперечных сил. Если поперечная сила, изменяясь непрерывно, проходит через нулевое значение, то необходимо определить аппликату (z) сечения, где Q обращается в нуль;
6) применяя метод сечений, вычислить значения изгибающих моментов в характерных сечениях и построить эпюру изгибающих моментов;
7) для определения экстремальных значений изгибающих моментов дополнительно определить моменты в сечениях, где эпюра поперечных сил проходит через нулевое значение;
8) определить из условия прочности осевой момент сопротивления сечения балки в сечении, где изгибающий момент имеет наибольшее по модулю значение;
9) используя формулы для определения осевых моментов сопротивления простых плоских сечений (прямоугольник, круг), определить размеры поперечного сечения балки (ПРИЛОЖЕНИЕ 1, табл.2; ПРИЛОЖЕНИЕ 2, табл. 2, табл.3).
Контрольные вопросы:
1. В каком случае балка работает на изгиб.
2. Что такое чистый и поперечный изгиб. Какие внутренние силовые факторы возникают в поперечных сечениях бруса в этих случаях.
3. Каким методом определяются внутренние силовые факторы, действующие в поперечных сечениях при изгибе.
4. Чему равны поперечная сила и изгибающий момент в произвольном сечении балки при изгибе.
5. Для чего строят эпюры Qy и Mx.
6. Укажите правило знаков для поперечной силы Q y’ изгибающего момента Mx ’.
7. Какими линиями очерчиваются эпюры Qy и Mx на участке действия равномерно распределённой нагрузки.
8. Что можно сказать про эпюры Qy и Mx для участка балки, испытывающего чистый изгиб.
9. По каким формулам определяются нормальные напряжения при поперечном изгибе.
10. Напишите формулы для определения осевых моментов сопротивления при изгибе для прямоугольника, круга и кольца.
Пример выполнения задания.
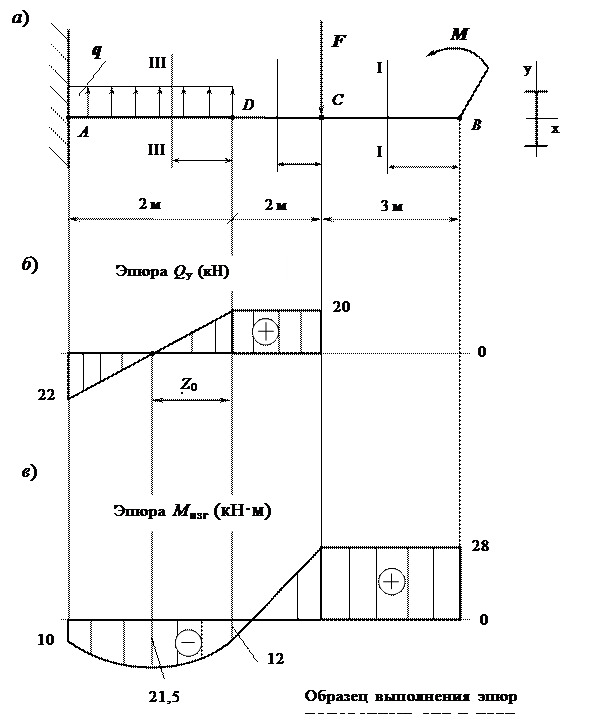
Жестко заделанная консольная балка АВ нагружена, как показано на расчетной схеме. Построить эпюры Q y и M изг, подобрать сечение в форме двутавра. Дано: F = 20 кН; q = 21 кН/м; М = 28 кН∙м; [ σ ] = 160 МПа.
1. Изобразим балку с действующими нагрузками.
2. Делим балку на участки по характерным сечениям В, С, D, A.
3. Определяем в характерных сечениях значения поперечной силы Q у и в выбранном масштабе строим эпюру:
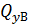 = 0;
= 0;
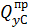 = 0;
= 0; 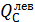 = 20 кН;
= 20 кН;
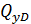 = 20 кН;
= 20 кН;
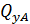 = 𝐹 – 𝑞
= 𝐹 – 𝑞  2 = 20 – 21
2 = 20 – 21  2 = – 22 кН.
2 = – 22 кН.
4. Определяем положение точки 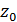 из подобия треугольников полученных на эпюре продольных сил, на участке 𝐴𝐷:
из подобия треугольников полученных на эпюре продольных сил, на участке 𝐴𝐷:
 =
= 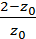 ; 22
; 22 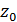 = 40 - 20
= 40 - 20 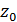 ; откуда
; откуда 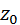 =
= 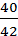 = 0,95 м.
= 0,95 м.
5. Вычисляем в характерных сечениях значения изгибающего момента 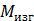 и в выбранном масштабе строим эпюру:
и в выбранном масштабе строим эпюру:
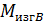 = 𝑀 = 28 кН∙м;
= 𝑀 = 28 кН∙м;
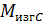 = 𝑀 = 28 кН∙м;
= 𝑀 = 28 кН∙м;
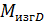 = 𝑀 – 𝐹
= 𝑀 – 𝐹 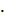 2 = 28 – 20
2 = 28 – 20  2 = – 12 кН∙м;
2 = – 12 кН∙м;
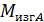 = 𝑀 – 𝐹
= 𝑀 – 𝐹 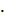 4 + 𝑞
4 + 𝑞 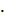 2
2 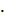
 = 28 – 20
= 28 – 20 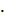 4 + 21
4 + 21  2
2  1 = – 10 кН∙м.
1 = – 10 кН∙м.
Исходя из эпюры М изг: ê М изг maxú = 28 кН  м = 28·106 Н·мм.
м = 28·106 Н·мм.
5. Определяем осевой момент сопротивления сечения:
W изг ≥ ê М изг maxú/[ σ ]; W x ≥ 28000000/160 ≥ 175000 мм3 ≥ 175 см3.
По ГОСТ 8239 – 89 выбираем двутавр № 20 с W х=184 см3.
|