Теорема о нормальной форме

Пусть - регулярная особая точка уравнения . Тогда существует диффеоморфизм окрестности точки плоскости на окрестность точки плоскости , приводящий уравнение 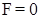к виду , где .

Стоит также добавить некое пояснение данной теоремы. Уравнение 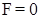задает поверхность в трехмерном пространстве линейных элементов на плоскости . Диффеоморфизм плоскости переводит каждый линейный элемент в новый линейный элемент. Утверждается, что часть поверхности 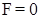вблизи регулярной особой точки можно перевести в часть поверхности вблизи точки .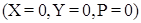

Доказательство теоремы основывается на пяти основных пунктах.

Первое – редукция к случаю, когда криминантой является ось . Пусть - регулярная особая точка уравнения . Тогда дискриминантная кривая в окрестности точки гладкая. Рассмотрим проекции контактных плоскостей в точках криминанты на плоскость . Мы получим в окрестности точки гладкое семейство прямых, не касающихся дискриминантной кривой.

Выберем теперь локальную систему координат на плоскости вблизи точки так, чтобы 1) дискриминантная кривая имела уравнение ; 2) линии пересекали дискриминантную кривую по построенным только что направлениям.

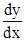Эти координаты мы будем по-прежнему обозначать через ; производная по-прежнему будет обозначаться через . Особая точка получает теперь координаты

Анализ условий регулярности.

Криминанта, согласно нашему выбору системы координат, является осью : на ней . Из этого следует, что для нашего уравнения записанного в введенных координатах, . Условие регулярности криминанты имеет теперь вид

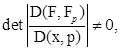т.е. ,

(так как в точка криминанты ). Далее, в точках крминанты . Следовательно, условие регулярности криминанты запишется в виде

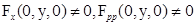Условие некасания с контактной плоскостью выполнено автоматически.

Разложим в ряд Тейлора по с остаточным членом степени 2:

Из полученных выше соотношений следует, что 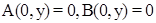. Поэтому мы можем записать

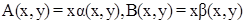, где и 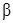- гладкие функции.

Условия регулярности криминанты имеют вид . Мы можем даже предположить для дальнейшего, что (если это не так, сменим знаки и/или ). Итак, .

Исследование квадратного уравнения.

Рассмотрим соотношение 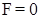как квадратное уравнение относительно с коэффициентами . Мы получаем

где есть функция от ; при этом .

Пусть, наконец, . Тогда получаем, оставляя лишь знак « » в « »,

Применим к этому уравнению относительно теорему о неявной функции. Получим решение , где гладкая функция, .

Дифференциальное уравнение для .

Заметим, что . Поэтому мы получили дифференциальное уравнение для :

, . (2)

Интегральные кривые на плоскости пересекают ось , имея с линиями касание второго порядка. Поэтому уравнение имеет первый интеграл вида , где - гладкая функция, ( - координата точки пересечения с осью ; , так как ).