Нижняя и верхняя цена игры

КОНЕЧНЫЕ ПАРНЫЕ ИГРЫС НУЛЕВОЙ СУММОЙ

Платежная матрица. Некоторые примеры

Конечных игр

Конечная игра n×m, описанная в нормальной форме, может быть представлена платежной матрицей, приведенной на рис.1.4. Элементами этой матрицы являются пара чисел, первое из которых W¹_ij определяет величину выигрыша игрока 1 (игрока А) при применении этим игроком i-ой стратегии, игроком 2 (игроком В) - j-ой стратегии. Второе число W²_ij определяет выигрыш игрока 2 (игрока В) при применении игроками тех же стратегий. Для упрощения записи выигрыш игрока А при i-ой стратегии игрока А и j-ой стратегии игрока В обозначается a_ij, выигрыш игрока В при тех же стратегиях - b_ij, сами стратегии записывают в виде А_i и В_j, соответственно.

Как было отмечено в разделе 1.3, существуют игры, в которых общая сумма выигрышей игроков равна нулю, т.е. выигрыш одного из игроков равен проигрышу (возможно и поражению) другого, т.е. налицо прямой конфликт между игроками. Такие игры называются играми с нулевой суммой или антагонистическими играми. В этих играх можно записать

a_ij + b_ij = 0, то есть a_ij = - b_ij

Рассмотрим парную конечную игру с нулевой суммой. Пусть игрок А располагает n личными стратегиями, которые обозначим A₁, A₂,..., A_n, игрок В - m личными стратегиями, обозначим их B₁,..., В_m. Говорят, что игра имеет размерность n×m. В результате выбора игроками любой пары стратегий A_i и B_j (i = 1,n, j=1,m) однозначно определяется исход игры, т.е. выигрыш аij игрока А (положительный или отрицательный) и проигрыш (-a_ij) игрока В. Предположим, что значения а_ij известны для любой пары стратегий (A_i, B_j).

В такой ситуации, если игра представлена в нормальной форме, вполне достаточно исследовать платежную матрицу только игрока А, которая может быть представлена в виде, приведенном в таблице 2.1, либо в виде матрицы А = {а_ij}, i = 1,n; j = 1,m, элементами которой являются выигрыши a_ij, соответствующие стратегиям A_i и B_j.

 

Таблица 2.1

Платежная таблица игры nm Платежная матрица игры n×m

Вj Аi

В1

В2

...

Вj

...

Bm

A1

a11

a12

...

a1j

...

a1n

a11

a12

...

a1j

...

a1n

A2

a21

a22

...

a2j

...

a2n

a21

a22

...

a2j

...

a2n

.

...

...

...

...

...

...

A=

...

...

...

...

...

...

Ai

Ai1

ai2

...

aij

...

aim

Ai1

ai2

...

aij

...

aim

.

...

...

...

...

...

...

...

...

...

...

...

...

An

an1

an2

...

anj

...

anm

an1

an2

...

anj

...

anm

Рассмотрим несколько элементарных примеров игр.

Пример 2.1. Составим платежную матрицу для игры “поиск”. Игрок А может спрятаться в одном из двух укрытий (I или II); игрок В ищет игрока А, и если найдет, то получает штраф 1 ден.ед. от А, в противном случае платит 1 ден. ед. игроку А.

Необходимо построить платежную матрицу игры.

Решение. Для составления платежной матрицы следует проанализировать поведение каждого из игроков.

Рассмотрим возможные стратегии игроков:

А₁ - игрок А прячется в укрытии I;

А₂ - игрок А прячется в укрытии II;

В₁ - игрок В ищет игрока А в укрытии I;

В₂ - игрок В ищет игрока А в укрытии II.

Рассмотрим комбинации стратегий сторон и определим соответствующие выигрыши сторон:

А₁-В₁ - игрок А прячется в укрытии I и там его обнаруживает игрок В, игрок А платит штраф, т.е. a₁₁ = -1.

А₁-В₂ - игрок А прячется в укрытии I, игрок В ищет его в укрытии II и не находит его там, игрок А получает штраф, т.е. a₁₂ = 1.

А₂-В₁ - игрок А прячется в укрытии II, игрок В ищет его в укрытии I и не находит его там, игрок А получает штраф, т.е. a₂₁ = 1.

А₂-В₂ - игрок А прячется в укрытии II и там его обнаруживает игрок В, игрок А платит штраф, т.е. a₂₂ = -1.

Таким образом, для игры “поиск” размера 2×2 получаем платежную матрицу

-1 1

А=

1 -1

Пример 2.2. Два игрока А и В, не глядя друг на друга, кладут на стол по монете вверх гербом или цифрой, по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или у обоих цифра), то игрок А забирает обе монеты; иначе их забирает игрок В. Требуется проанализировать игру и составить ее матрицу, считая выигрыш монеты за +1.

Решение. Игра состоит только из двух ходов: наш ход (игрок А) и ход противника (игрок В), оба личные. Игра не принадлежит к играм с полной информацией, так как в момент хода игрок не знает, что сделал другой.

У нас две стратегии: А₁ - выбирать герб и А₂ - выбирать цифру; у противника такие же две стратегии: В₁ - герб и В₂ - цифра. Таким образом, данная игра есть игра 2×2.

Матрица игры приведена в табл.2.2.

 

Таблица 2.2. Таблица 2.3.

В А	В1 (г)	В2(ц)		В А	В1	В2	В3
А1 (г)		-1		А1		-3
А2 (ц)	-1			А2	-3		-5
				А3		-5

 

Пример 2.3. Игроки А и В одновременно и независимо друг от друга записывают каждый одно из трех чисел: 1, 2 или 3. Если сумма написанных чисел четная, то В платит А эту сумму в рублях; если она нечетная, то, наоборот, А платит В эту сумму.

Требуется проанализировать игру и составить ее матрицу.

Решение. Игра состоит из двух ходов; оба - личные. У нас (А) три стратегии: А₁ -писать 1; А₂ -писать 2; А₃ -писать 3. У противника (В) - те же три стратегии. Игра представляет собой игру 3×3 с матрицей, приведенной в табл. 2.3.

Пример 2.4. В нашем распоряжении имеются три вида вооружения: А₁, А₂, А₃; у противника - три вида самолетов: В₁, В₂, В₃. Наша задача поразить самолет; задача противника сохранить его непораженным. При применении вооружения А₁ самолеты В₁, В₂, В₃ поражаются соответственно с вероятностями 0,9, 0,4, 0,2; при вооружении А₂ - с вероятностями 0,3, 0,6 и 0,8; при вооружении А₃ - с вероятностями 0,5, 0,7 и 0,2. Требуется сформулировать ситуацию в терминах теории игр.

Решение. Ситуация может рассматриваться как игра 3×3 с двумя личными ходами и одним случайным. Наш личный ход - выбор типа вооружения; личный ход противника - выбор самолета для участия в бою. Случайный ход - применение вооружения; этот ход может закончиться поражением или непоражением самолета. Наш выигрыш равен единице, если самолет поражен, и равен нулю в противном случае. Нашими стратегиями являются три варианта вооружения; стратегиями противника- три варианта самолетов.

Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения каждого самолета данным оружием. Матрица игры приведена в таблице 2.4.

Таблица 2.4.

В А	В1	В2	В3
А1	0,9	0,4	0,2
А2	0,3	0,6	0,8
А3	0,5	0,7	0,2

Нижняя и верхняя цена игры

Рассмотрим игру n×m с матрицей A = а_ij, i =1,n; j =1,m; и определим наилучшую среди стратегий A₁, A₂,..., A_n.

Выбирая стратегию A_i, игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий B_j, для которой выигрыш для игрока А минимален (игрок В стремится “навредить” игроку А). Обозначим через a_i наименьший выигрыш игрока А при выборе им стратегии A_i для всех возможных стратегий игрока В (наименьшее число в i-й строке платежной матрицы), т.е. (2.1)

Игрок А, зная о такой тактике игрока В, стремится выбирать свою стратегию таким образом, чтобы максимизировать свой минимальный выигрыш, т.е. среди всех чисел α_i (i=1,n) выберем наибольшее:

Следовательно, 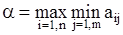(2.2)

Данная наибольшая величина из наименьших значений выигрыша игрока А α называется нижней ценой игры, или максиминным выигрышем (максимином).

Это гарантированный выигрыш игрока А при любой стратегии игрока В.

Стратегия, соответствующая максимину, называется максиминной стратегией.

В то же время игрок А, на любую выбранную игроком В стратегию В_j старается ответить такой своей стратегией, чтобы максимизировать проигрыш игрока В (стремится “навредить” игроку В).

Обозначим через β_j наибольший проигрыш игрока В (или что то же самое - наибольший выигрыш игрока А) при выборе игроком В его стратегии В_j для всех возможных стратегий игрока А (наибольшее число в j-м столбце платежной матрицы)

(2.3)

Игрок В, зная о такой тактике игрока А, при выборе своей стратегии стремится поступать таким образом, чтобы минимизировать свой максимальный проигрыш, т.е. среди всех чисел β_j (j=1,m) выберем наименьшее:

Следовательно, (24)

Эта величина β называется верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Стратегия, соответствующая минимаксу, называется минимаксной стратегией.

Принцип, диктующий игрокам выбор наиболее “осторожных” минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника, и гарантирует игроку А выигрыш не менее максиминного выигрыша, а игроку В - проигрыш не более минимаксного.

Пример 2.5. Определим нижнюю и верхнюю цены игры и соответствующие стратегии в задаче 2.4. Рассмотрим платежную матрицу

Таблица 2.5.

В А	В1	В2	В3	αi
А1	0,9	0,4	0,2	0,2
А2	0,3	0,5	0,8	0,3
А3	0,5	0,6	0,2	0,2
βj	0,9	0,6	0,8	α=0,3 β=0,7

При выборе стратегии А₁ (первая строка матрицы) минимальный выигрыш игрока А равен α₁ = min(0,9; 0,4; 0,2) = 0,2 и соответствует стратегии В₃ игрока В. При выборе стратегии А₂ (вторая строка матрицы) минимальный выигрыш равен a₂ = min(0,3; 0,6; 0,8) = 0,3, он достигается при стратегии B₁. При выборе стратегии А₃ (третья строка матрицы) минимальный выигрыш равен a₃=min (0,5; 0,7; 0,2) = 0,2, он достигается при стратегии B₃.

Нижняя цена игры a= max(a₁, a ₂, a₃)= mах(0,2; 0,3; 0,2) = 0,3, т.е. гарантируя себе максимальный выигрыш при любой стратегии игрока В, игрок А должен выбрать стратегию A₂, т.е. А₂ является наиболее осторожной (максиминной) стратегией игрока А; пользуясь этой стратегией он гарантирует себе, что будет поражать самолеты в среднем не менее, чем 0,3 (30%) всех случаев.

Рассмотрим возможные стратегии игрока В. Выбирая стратегию B1 (первый столбец таблицы), игрок В понимает, что игрок А ответит стратегией А₁, чтобы максимизировать свой выигрыш (проигрыш игрока B). Следовательно, максимальный проигрыш игрока В при выборе им стратегии B₁ равен β₁ = max(0,9; 0,3; 0,5) = 0,9. Аналогично, максимальный проигрыш игрока В (выигрыш А) при выборе им стратегии B₂ (второй столбец) равен β₂ = mах(0,4; 0,5; 0,6) = 0,6. При выборе стратегии В₃ максимальный проигрыш игрока В равен β₃ = max(0,2; 0,8; 0,2) = 0,8.

Верхняя цена игры β = min(0,9; 0,6; 0,8) = 0,6, наиболее осторожной (минимаксной) стратегией игрока В является В₂; применяя этот самолет, противник может быть уверен, что он будет поражаться не более чем в 0,6 (60%) всех случаев.

Нетрудно заметить, что в проведенном анализе каждая из сторон была ориентирована на худшую с ее точки зрения ситуацию - минимальный выигрыш или максимальный проигрыш при любой фиксированной стратегии. Обе стороны должны были улучшить, насколько возможно, свое положение, выбирая максиминную и минимаксную стратегии с целью ослабить (и даже исключить) зависимость получаемых результатов от действий противника. В этом находит свое выражение принцип гарантированного результата, предполагающего, как было замечено, отсутствие риска и связанных с ним нежелательных последствий.

На этом примере удобно продемонстрировать одно важное свойство минимаксных стратегий - их неустойчивость. Пусть мы (игрок А) применяем свою наиболее осторожную (максиминную) стратегию А₂, а противник свою наиболее осторожную (минимаксную) стратегию В₂. До тех пор, пока оба противника придерживаются этих стратегий, средний выигрыш равен 0,5; он больше нижней, но меньше верхней цены игры. Теперь допустим, что противнику стало известно, что мы применяем стратегию А₂; он немедленно ответит на нее стратегией В₁ и сведет выигрыш к 0,3. В свою очередь, на стратегию В₁ у нас есть хороший ответ: стратегия А₁, дающая нам выигрыш 0,9 и т.д.

Таким образом, положение, при котором оба игрока пользуются минимаксными стратегиями, является неустойчивым и может быть нарушено поступившими сведениями о стратегии противной стороны.

2.3. Проблема равновесия в игре [4/81, 9/213]

В задаче 2.5, рассмотренной выше, верхняя и нижняя цены игры различны: a≠β. Такие игры, как убедились, являются неустойчивыми.

Существует класс игр, для которых минимаксные стратегии являются устойчивыми. Это те игры, для которых нижняя цена равна верхней, то есть, a=β.

Если верхняя и нижняя цены игры совпадают, то их общее значение называется чистой ценой игры, или ценой игры, и обозначают греческой буквой n (нью). Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность - оптимальным решением, или решением игры.

В этом случае игрок А получает максимальный гарантированный (не зависящий от поведения игрока В) выигрыш n, а игрок B добивается минимального гарантированного (вне зависимости от поведения игрока А) проигрыша n.

Пара чистых стратегий A_i и B_j дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент aij является одновременно минимальным в своей строке и максимальным в своем столбце.

В геометрии точку на поверхности, обладающую аналогичным свойством (одновременный минимум по одной координате и максимум по другой), называют седловой точкой; (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз - в другом). Этот термин применяется и в теории игр. Элемент матрицы, обладающий этим свойством, называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.

Обозначим А* и B* - пару чистых стратегий, на которых достигается решение игры в задаче с седловой точкой. Введем функцию выигрыша первого игрока на каждой паре стратегий: P(A_i,B_j)=a_ij. Тогда из условия оптимальности в седловой точке выполняется двойное неравенство:

P(A_i,B*) ≤ P(А*,В*) ≤ P(A*,B_j),

которое справедливо для всех i= 1, n, j= 1, m.

Это утверждение легко проверить на примере игры с седловой точкой.

Пример 2.6. Определить нижнюю и верхнюю цену игры, заданной платежной матрицей

	0,5	0,6	0,7
А =	0,9	0,6	0,8
	0,8	0,7	0,75

Имеет ли игра седловую точку?

Решение. Все расчеты удобно проводить в таблице, в которой, кроме матрицы A, введены столбец a_i, и строка β_j (табл. 2.6). Анализируя строки матрицы (стратегии игрока А), заполняем столбец a_i: a₁ = 0,5, a₂ = 0,6, a₃ = 0,7 - минимальные числа в строках 1, 2, 3. Аналогично β_j = 0,9, β₂ = 0,7, β₃ = 0,8 - максимальные числа в столбцах 1, 2, 3, соответственно.

Таблица 2.6

В А	В1	В2	В3	αi
А1	0,5	0,6	0,7	0,5
А2	0,9	0,6	0,8	0,6
А3	0,8	0,7	0,75	0,7
βj	0,9	0,7	0,8	α=0,7 β=0,7

Нижняя цена игры α = max a_i = max (0,5; 0,6; 0,7) = 0,7 (наибольшее число в столбце ai) и верхняя цена игры β = min β_j = min (0,9; 0,7; 0,8) = 0,7 (наименьшее число в строке β_j). Эти значения равны, т.е. a. = β, и достигаются на одной и той же паре стратегий (А₃, В₂). Следовательно, игра имеет седловую точку A₃, B₂) и цена игры n = 0,7.

В случае игры с седловой точкой минимаксные стратегии обладают своеобразной “устойчивостью”: если одна сторона придерживается своей минимаксной стратегии, то для другой может быть только невыгодным отклоняться от своей. Заметим, что в этом случае наличие у любого игрока сведений о том, что противник избрал свою оптимальную стратегию, не может изменить собственного поведения игрока: если он не хочет действовать против своих же интересов, он должен придерживаться своей оптимальной стратегии. Любое отклонение от оптимальной стратегии приводит отклоняющегося игрока к невыгодным последствиям, вынуждающим его вернуться в исходное положение.

Положение, при котором ни одна из сторон не имеет никаких разумных оснований для изменения своей стратегии, называется ситуацией равновесия [8/214].

В играх с седловой точкой такая ситуация возникает и сохраняется сколь угодно долго, если стороны А и В используют соответствующие стратегии, называемые в этом случае чистыми стратегиями.

Итак, для каждой игры с седловой точкой существует решение, определяющее пару оптимальных стратегий обеих сторон, отличающуюся следующими свойствами:

1) если обе стороны придерживаются своих оптимальных стратегий, то средний выигрыш равен чистой цене игры, одновременно являющейся ее нижней и верхней ценой;

2) если одна из сторон придерживается своей оптимальной стратегии, а другая отклоняется от своей, то от этого отклоняющаяся сторона может только потерять и ни в коем случае не может увеличить свой выигрыш.

Класс игр, имеющих седловую точку, представляет большой интерес как с теоретической, так и с практической точки зрения.

В теории игр доказывается следующая теорема:

Теорема 2.1. Каждая игра с полной информацией имеет седловую точку и, следовательно, каждая такая игра имеет решение, т.е. существует пара оптимальных стратегий той и другой стороны, дающая средний выигрыш, равный цене игры [3/20].

Могут встретиться случаи, когда платежная матрица имеет несколько седловых точек, однако это не изменит характера рекомендуемых решений.

 

Смешанные стратегии

На практике наиболее распространенным является случай, когда платежная матрица не имеет седловой точки, т.е. a¹b. Ситуации, которые могут при этом возникнуть, мы рассмотрели в задаче 2.5 (раздел 2.2). Анализируя матрицы таких игр, пришли к заключению, что, если каждому игроку предоставлен выбор одной - единственной стратегии, то в расчете на разумно действующего противника этот выбор должен определяться принципом минимакса. Придерживаясь своей максиминной стратегии, мы при любом поведении противника заведомо гарантируем себе выигрыш, равный нижней цене игры a. Возникает естественный вопрос: нельзя ли гарантировать себе средний выигрыш, больший a, если применять не одну-единственную чистую стратегию, а чередовать случайным образом несколько стратегий?

Кроме того, как отмечено выше, игры в чистых стратегиях часто оказываются неустойчивыми в случае информированности сторон о действиях друг друга.

В таких ситуациях каждой стороне необходимо как-то скрыть свое поведение от противника, чтобы ослабить влияние информационного фактора и получить желаемое преимущество. Это трудно осуществить, ориентируясь только на разумный выбор конкретных стратегий, так как любые рассуждения могут быть воспроизведены противником. В то же время полный отказ от рационального начала и переход, например, к бессистемному поиску вариантов решений означал бы прекращение игры как таковой и замену ее неуправляемым случайным процессом.

Приемлемый компромисс достигается здесь путем обоснованного, разумного введения элемента случайности в действия сторон так, что каждый отдельный ход остается непредсказуемым, но вся совокупность ходов обладает вполне определенными, заранее заданными свойствами. Другими словами участники конфликта чередуют (смешивают) в случайном порядке свои стратегии в соответствии со специально разработанной схемой, обеспечивающей нужную частоту (вероятность) реализации каждой из А₁, А₂,...,А_n, B₁, B₂,...,B_m стратегий.

Такие комбинированные стратегии, состоящие в применении нескольких стратегий, чередующих по случайному закону с определенным соотношением частот, называются смешанными стратегиями [5/21].

Говоря языком теории вероятностей, можно ситуацию сформулировать следующим образом. Пусть a_ij - матрица игры размера n´m.

Если p_i - вероятность появления события A_i (события, состоящего в том, что игрок А выберет стратегию A_i), то можно говорить о распределении вероятностей на множестве стратегий стороны А, причем всегда

(2.5)

то есть, событие, состоящее в реализации некоторой допустимой стратегии на очередном ходе, является достоверным.

Очевидно, каждая чистая стратегия является частным случаем смешанной, в которой все стратегии, кроме одной, применяются с нулевыми частотами (вероятностями), а данная - с частотой (или вероятностью), равной 1.

Оказывается, что, применяя не только чистые, но и смешанные стратегии, можно для каждой конечной игры получить решение, т.е. пару таких (в общем случае смешанных) стратегий, что при применении их обоими игроками выигрыш будет равен цене игры, а при любом одностороннем отклонении от оптимальной стратегии выигрыш может изменяться только в сторону, невыгодную для отклоняющегося.

Высказанное утверждение составляет содержание так называемой теоремы о минимаксе - основной теоремы теории игр, доказанной фон Нейманом в 1928 году. Известные доказательства теоремы весьма сложны; поэтому приведем только ее формулировку:

В конечной игре двух лиц с нулевой суммой и полной информацией имеется, по крайней мере, одно решение в области смешанных стратегий, то есть, имеет место равенство P_a= P_b при a¹b [8/219,3/21].

Теорема о минимаксе указывает на существование ситуации равновесия для случая a¹b и, следовательно, оптимальных стратегий S*_a, S*_b, т.е. решений игры, позволяющих добиваться среднеожидаемого выигрыша n = P_a = P_b. Величина n называется ценой игры. Из приведенных выше оценок следует a≤n≤b. (2.6)

Действительно, a есть минимальный гарантированный выигрыш, который мы можем себе обеспечить, применяя только свои чистые стратегии. Так как смешанные стратегии включают в себя в качестве частного случая и все чистые, то, допуская, кроме чистых, еще и смешанные стратегии, мы, во всяком случае, не ухудшаем своих возможностей; следовательно, n≥a.

Аналогично, противник, применяя чистые и смешанные стратегии, не увеличивает свой проигрыш, т.е. n≤b, откуда следует неравенство (2.6).

Введем специальное обозначение для смешанных стратегий.

Смешанной стратегией S_a игрока А называется применение чистых стратегий A₁, A₂,..., A_i,..., A_n с вероятностями p₁, p₂,..., p_i,...,p_n, причем сумма вероятностей равна 1, то есть . Смешанные стратегии игрока А записываются в виде матрицы

	A1	A2	…	Ai	…	An
Sa =
	p1	p2	…	pi	…	pn

или в виде строки S_a = (p₁, p₂,..., p_i,..., p_n,). Аналогично смешанные стратегии игрока В обозначаются:

	B1	B2	…	Вj	…	Вm
Sb =							или Sb=(q1, q2, … qj,… qm),
	q1	q2	…	qj	…	qm

где сумма вероятностей появления стратегий равна 1, то есть .

Пусть S*_a = (p*₁, p*₂,..., p*_n) и S*_b = (q*₁, q*,₂..., q*_m) - пара оптимальных стратегий. В общем случае не все чистые стратегии, доступные данному игроку, входят в его оптимальную смешанную стратегию, а только некоторые. Чистые стратегии, входящие в оптимальную смешанную стратегию игрока с отличной от нуля вероятностью, называются его активными или полезными стратегиями.

Оказывается, что решение игры обладает еще одним замечательным свойством, сформулированным в теореме об активных стратегиях:

Теорема 2.2. Если один из участников игры придерживается своей оптимальной смешанной стратегии, то ожидаемый выигрыш останется неизменным и равным n независимо от характера действий другого участника в пределах его активных стратегий.

Противник при этом, например, может пользоваться любой из своих активных ("полезных") стратегий в чистом виде, а также может смешивать их в любых пропорциях.

Теорема имеет большое практическое значение - она дает конкретные модели нахождения оптимальных стратегий при отсутствии седловой точки.