Распределение скоростей на вертикали и в живом сечении

 

Средние в живом сечении скорости движения воды в реках невелики. У равнинных рек с песчаным дном они обычно лежат в интервале 0,5-1,5 м/с. В меженный период в плесовых лощинах рек с малыми уклонами средние скорости могут уменьшаться до 0,3-0,1 м/с. С увеличением уклонов в реках растет крупность донных отложений и растут скорости. У горных рек, имеющих валунно-галечное дно, средние скорости могут составлять 5-7 м/с и более.

Местные скорости (т.е. осредненные скорости в отдельных точках сечений) меняются, конечно, в более широких границах. В результате действия сил трения скорости течения в открытых потоках убывают от свободной поверхности к дну, а также от середины сечения к берегам. В гидромеханике доказывается, что вблизи твердой поверхности осредненные скорости турбулентного потока изменяются как логарифм расстояния от этой поверхности. Распространение логарифмического закона на всю вертикаль представляет собой условное допущение, однако оно не приводит к существенной погрешности. В результате имеем следующую формулу распределения осредненных скоростей на вертикали:

. (52)

Здесь u_max – максимальная (поверхностная) скорость; c – безразмерная величина, известная под названием параметра Кармана (названа так по имени одного из крупнейших гидромехаников XX столетия Т. Кармана).

Плоскость, от которой отсчитываются расстояния h, проведена не по поверхности дна, а ниже ее на величину, равную среднему диаметру d частиц грунта, покрывающих дно. Таким образом, формула (52) действительна в области расстояния от 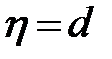до .

На поверхности дна, т.е. при , получаем конечное положительное значение скорости (рис. 23).

Рис.23. Эпюра логарифми- ческого распределения скоростей на вертикали

Подставив выражение по формуле (52) в формулу средней скорости на вертикали (40) и выполнив интегрирование в пределах от d до h, получаем

. (53)

Найдем теперь высоту h' той точки, на которой местная осредненная скорость равна средней на вертикали. Для этого достаточно приравнять правые части формул (52) и (53), предварительно заменив в выражении (52) h на h'.

Из этого уравнения находим

.

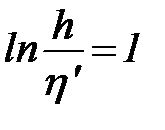или

. (54)

В гидрометрии этот результат округляют до . Измерения скорости в одной этой точке в принципе достаточно для определения средней скорости на вертикали.

При практическом пользовании формулой (52) удобно перейти от натуральных логарифмов к десятичным. Кроме того, для упрощения записи в гидромеханике принято величину , имеющую размерность скорости, обозначать одной буквой .

Так как величина

. (55)

характеризует силу трения, то ее называют динамической скоростью (она не является, очевидно, скоростью движения какого-нибудь материального объекта). Введя, наконец, опытное значение параметра Кармана , получим формулу распределения скоростей на вертикали в следующем расчетном виде:

. (56)

Рис. 24. Эпюры распределения скоростей на вертикали

Вывод логарифмического закона распределения скоростей основан на предположении о плоскопараллельном (равномерном) движении жидкости. Это условие в естественных потоках удовлетворяется редко и поэтому эпюры скоростей, получаемые в результате измерений, могут заметно отклоняться от распределения (56). Наиболее сильные нарушения теоретического распределения возникают вследствие резких изменений площадей поперечных сечений потока и под воздействием ветра на свободную поверхность.

При резком изменении площадей поперечных сечений скорости течения у дна и у свободной поверхности меняются не одинаково. При стеснении потока, например, на участке реки, сжатом выходами в берегах скальных пород, донная скорость растет быстрее, чем поверхностная, и в результате эпюра скоростей на вертикали выравнивается (рис. 24). Это происходит и тогда, когда поток стеснен в вертикальном направлении, например при ускоренном движении воды над резким возвышением дна.

Если поток расширяется, донная скорость убывает быстрее, чем поверхностная, и поэтому эпюра скоростей растягивается, делается менее равномерной (см. рис. 24).

При внезапном сжатии потока донная скорость может стать больше поверхностной. При внезапном расширении она может стать отрицательной. В этом случае в нижних слоях потока образуется зона отрыва и донные скорости направлены против основного течения.

Ветер, создавая волны на свободной поверхности, делает эту поверхность шероховатой и поэтому на ней может возникать довольно большая сила трения. Эта сила трения, в зависимости от направления ветра (по течению или напротив) может ускорять или тормозить поверхностные слои потока. Результатом такого ускорения или торможения является искажение эпюр распределения скоростей, показанное на рис. 25.

Рис. 25. Изменение эпюр распределения скоростей под влиянием попутного или встречного ветра

Появление на реке ледяного покрова приводит к созданию поля скоростей, характерного для напорных потоков. Максимум осредненных скоростей переходит в толщу потока. Положение этого максимума определяется соотношением между шероховатостью дна и шероховатостью нижней поверхности ледяного покрова. Как уже отмечалось, шероховатость нижней поверхности льда меняется во времени. При бурном осеннем ледоходе образование ледяного покрова сопровождается торошением и наползанием льдин друг на друга. В результате сразу после замерзания нижняя поверхность льда оказывается очень шероховатой и максимум скоростей смещается в нижнюю половину вертикали (рис. 26). Под действием течения и подвода тепла от дна шероховатость льда в дальнейшем снижается и максимум скоростей перемещается вверх.

Рис. 26. Эпюра распределения скоростей на вертикали подо льдом

Так как при одном и том же расходе воды площадь живого сечения подо льдом больше площади живого сечения открытого русла, то абсолютные значения скоростей течения в зимнее время малы. По грубой оценке они вдвое меньше скоростей, наблюдающихся в реке в летнюю межень.

Чтобы наглядно изобразить распределение скоростей в поперечном сечении потока, точки сечения, в которых скорости одинаковы, соединяют плавными линиями. Эти линии называются линиями равных скоростей, или изотахами. На рис. 27 представлено такое построение для открытого и закрытого русла.

 

Рис. 27. Изотахи в живых сечениях открытого (а)

и закрытого (б) русел