Критерий предложен американским ученым Найквистом в 1932 г. для исследования устойчивости усилителей с обратной связью. В 1938 г. А.В. Михайлов разработал методику его применения для исследования систем автоматического управления.
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по виду амплитудно-фазовой характеристики (АФЧХ) разомкнутой системы.
АФЧХ разомкнутой системы может быть получена как аналитически, так и экспериментально. Это обстоятельство выгодно отличает критерий Найквиста от ранее изложенных.
Ранее было введено понятие передаточной функции разомкнутой системы. Эта функция может быть представлена в виде
(4.18)
Причем степень числителя не может быть выше степени знаменателя, m£n. При подстановке р=iw получается частотная передаточная функция разомкнутой системы
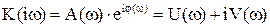. (4.19)
 |
Частотная передаточная функция разомкнутой системы представляет собой комплексное число. На основании рассмотренных ранее частотных характеристик смысл ее можно объяснить следующим образом. Представим себе систему регулирования в разомкнутом состоянии в виде некоторого звена с передаточной функцией W(р) (рис. 4.10).
Если на вход этого звена подавать сигнал ошибки в виде гармонических колебаний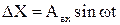 
с амплитудой Авх и частотой w, то в установившемся режиме на выходе регулируемая величина будет изменяться также по гармоническому закону 
с амплитудой Авых, той же частотой w и фазовым сдвигом j. Модуль частотной передаточной функции представляет собой отношение амплитуд выходной и входной величин:
 |
,
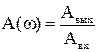а аргумент – сдвиг фаз j.
Если изменять частоту входного воздействия от -¥ до +¥ и откладывать на комплексной плоскости точки, соответствующие получающимся комплексным числам, то геометрическое место этих точек образует амплитудно-фазовую характеристику разомкнутой системы (рис. 4.11).
Ветвь этой характеристики, соответствующая отрицательным частотам, является зеркальным отражением ветви, соответствующей положительным частотам, относительно вещественной оси. На амплитудно-фазовой характеристике для удобства могут отмечаться точки, соответствующие определенным частотам, например w1, w2, w3 и т.д.
Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты w (рис. 4.11).
В реальных системах всегда удовлетворяется условие m<n. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к нулю и точка с частотой w=±¥ попадает в начало координат.
Сформулируем достаточные и необходимые требования к амплитудно-фазовой характеристике разомкнутой системы, при выполнении которых система автоматического регулирования в замкнутом состоянии будет устойчивой.
Ограничим вначале задачу и будем рассматривать только такие передаточные функции (4.18), которые соответствуют статическим системам. Это значит, что знаменатель (4.18) не будет иметь в качестве множителя оператор р.
Формулировка критерия для случая устойчивой в замкнутом состоянии системы. Замкнутая система будет устойчивой, если годограф вектора W(iw) или АФЧХ разомкнутой системы при изменении частоты w от 0 до ¥ не охватывает точку с координатами (-1; i0). Это является необходимым и достаточным условием того, чтобы система была устойчивой в замкнутом состоянии (рис. 4.12).
При определении устойчивости достаточно построить амплитудно-фазовую характеристику только для положительных частот, т. к. ее ветвь, соответствующая отрицательным частотам, может быть легко получена зеркальным отображением относительно оси вещественных координат.
На рис. 4.13 изображен случай так называемой абсолютно устойчивой системы. Этот термин означает, что система остается устойчивой при любом уменьшении коэффициента усиления разомкнутой цепи.
Если передаточную функцию разомкнутой статической системы (4.18) представить в виде (3.111):
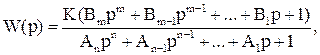
где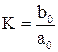 
,
то нетрудно видеть, что уменьшение общего коэффициента усиления K приводит к уменьшению модуля (4.19), а это в случае, изображенном на рис. 4.13, не может привести к охвату годографом точки (-1; i0).
На рис. 4.14 изображен случай так называемой условно устойчивой системы. Здесь система будет устойчивой при значении общего коэффициента усиления, лежащем в некоторых пределах. Как увеличение, так и уменьшение общего коэффициента усиления K может привести к охвату годографом точки (-1; i0), что будет соответствовать неустойчивости системы в замкнутом состоянии.
На рис. 4.15 изображен случай, когда система находится на границе устойчивости.
 |
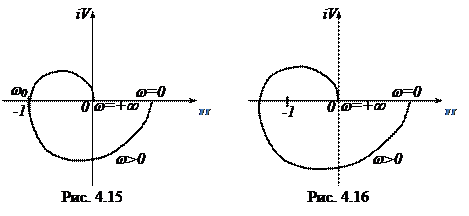Граница устойчивости будет колебательного типа. Это вытекает из того, что при некоторой частоте, при которой годограф пересекает точку (-1; i0), имеет место равенство
, что может быть записано в виде 
. Это выражение представляет собой характеристическое уравнение, которое обращается в нуль при подстановке р=iw0. Таким образом, чисто мнимый корень является решением характеристического уравнения. На рис. 4.16 изображен случай неустойчивой системы.
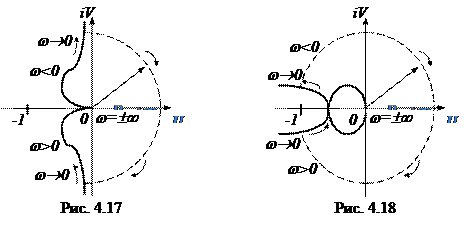
Обратимся теперь к передаточной функции разомкнутой системы, соответствующей астатизму первого (r=1) или более высоких порядков (r=k). В этом случае передаточная функция может быть представлена в виде
.
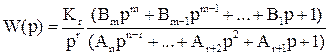Будем предполагать, что все корни знаменателя передаточной функции (кроме нулевого корня р=0) лежат в левой полуплоскости, т.е. в разомкнутом состоянии система является нейтрально устойчивой. Амплитудно-фазовая характеристика разомкнутой системы будет иметь разрыв непрерывности в точке w=0. В этой точке модуль А(0)®¥, а фаза делает скачок на r´1800 (r´p), т.е. АФЧХ на комплексной плоскости делает поворот по часовой стрелке.
На рис. 4.17 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы с астатизмом первого порядка. Характеристика начинается в начале координат при w®-¥ и затем уходит в бесконечность при w®0 (верхняя ветвь). Далее характеристика дополняется полуокружностью бесконечно большого радиуса так, чтобы вектор W(iw) повернулся по часовой стрелке на угол равный p.
Нижняя ветвь характеристики соответствует изменению частоты от 0 до +¥.
Нетрудно видеть, что характеристика не охватывает точку (-1; i0), и система в замкнутом состоянии будет устойчивой.
На рис. 4.18 изображена амплитудно-фазовая характеристика абсолютно устойчивой системы при наличии астатизма второго порядка. Так же как и ранее, здесь можно получить условную устойчивость (рис. 4.18), колебательную границу устойчивости, если характеристика пройдет через точку (-1; i0), и неустойчивость, если характеристика будет охватывать точку (-1; i0).
Обобщая проведенные рассуждения, получаем, что для определения устойчивости системы с астатизмом любого порядка достаточно построить только одну ветвь амплитудно-фазовой характеристики, соответствующую положительным частотам, которая должна быть дополнена окружностью бесконечно большого радиуса. При этом для устойчивой в замкнутом состоянии системы эта ветвь вместе с частью окружности, заключенной между положительной полуосью вещественных и амплитудно-фазовой характеристикой, соответствующей положительным частотам, не должна охватывать точку (-1; i0) в соответствии с рис. 4.19.
Из рис. 4.19 следует, что абсолютная устойчивость может быть получена при степени астатизма r£2. При большей степени астатизма может быть получена только условная устойчивость.
Большое практическое преимущество критерия Найквиста заключается также в том, что он может применяться при использовании логарифмических частотных характеристик, которые во многих случаях могут строиться почти без вычислительной работы. Этот вопрос будет рассмотрен далее.
В качестве иллюстрирующего примера рассмотрим следящую систему, изображенную на рис. 4.4. Для этой системы была получена передаточная функция разомкнутой системы:
.
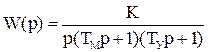Нетрудно видеть, что все корни знаменателя, кроме одного нулевого корня, лежат в левой полуплоскости. Поэтому в устойчивой системе амплитудно-фазовая характеристика не должна охватывать точку (-1, i0).
 |
Частотная передаточная функция
.
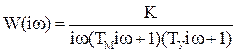Модуль ее
,
и фаза
.
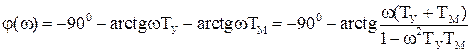Задаваясь различными значениями частоты от 0 до +¥ можно вычислить модуль и фазу. По модулю и фазе легко строится вектор W(iw) либо вычисляются предварительно вещественная и мнимая части частотной передаточной функции:
; 
.
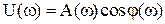Ввиду достаточно простого выражения для частотной передаточной функции в данном примере можно легко найти U(w) и V(w), разлагая непосредственно комплекс W(iw) на вещественную и мнимую части:
; 
.
Результаты расчетов сводятся в табл. 4.1.
Таблица 4.1
| w | А(w) | j(w) | U(w) | V(w) |
| ¥ | -900 |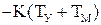 
| ¥ | |
| … | … | … | … | … |
| ¥ | -2700 |
Примерный вид амплитудно-фазовой характеристики в случае устойчивой замкнутой системы изображен на рис. 4.20.
Поскольку исходная передаточная функция имеет простой вид, задача получения устойчивости в рассматриваемой системе может быть решена в общем виде. Из рис. 4.20 следует, что для получения устойчивости точка пересечения амплитудно-фазовой характеристики с осью вещественных (точка А) должна лежать правее точки (-1; i0).
Это условие можно записать следующим образом:
 |
А(wА)<1.
Найдем частоту wА в точке А. Это можно сделать, взяв одно из условий V(wА)=0 или j(wА)=-1800, откуда получаем
.
Подстановка этой частоты в записанное выше неравенство дает
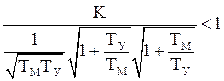
или после преобразования
.
Таким образом, получено условие, совпадающее с найденным ранее условием, вытекающим из критериев Гурвица и Михайлова.
Сделаем теперь два замечания, касающихся использования для определения устойчивости замкнутой системы передаточной функции разомкнутой системы.
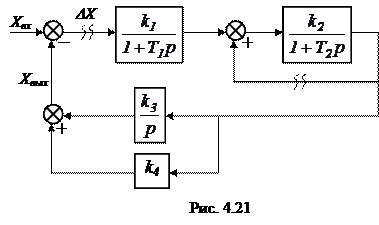
Замечание 1. В случае определения устойчивости многоконтурной системы регулирования размыкание ее для получения передаточной функции разомкнутой системы можно делать, вообще говоря, в произвольном месте. Рассмотрим, например, систему, структурная схема которой изображена на рис. 4.21.
Разомкнем систему на входе первого звена. Тогда, рассматривая точку A как вход, а точку B как выход, получаем передаточную функцию разомкнутой системы
.
Разомкнем теперь ту же систему не на входе первого звена, а в цепи обратной связи второго звена (точка С соответствует входу, а точка D – выходу).
Передаточная функция разомкнутой системы в этом случае
.
 |
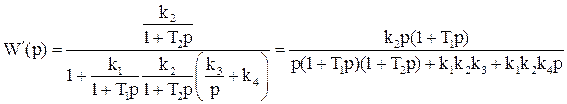Передаточные функции W(p) и W¢(p) получились различными. Однако им соответствует одно и то же характеристическое уравнение замкнутой системы
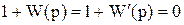, которое имеет вид:
.
Поэтому для определения устойчивости можно пользоваться передаточной функцией разомкнутой системы, полученной размыканием исходной системы в произвольной точке, в которой выполняется условие детектирования.
Однако передаточные функции W(p) и W¢(p) имеют различие. Только передаточная функция W(p) связывает между собой изображения регулируемой величины и ошибки, и только она связана с передаточной функцией замкнутой системы Ф(р) известным соотношением (3.13):
.
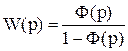Передаточную функцию при размыкании на входе первого звена в дальнейшем будем считать главной передаточной функцией разомкнутой системы и именно ее иметь в виду при рассмотрении методов определения качества регулирования и синтеза систем регулирования.
Замечание 2. При определении устойчивости в используемой передаточной функции разомкнутой системы можно перемещать члены знаменателя в числитель и наоборот, за исключением старшего члена знаменателя. Так, например, если имеется передаточная функция
.
то для расчета устойчивости она может быть заменена функцией
.
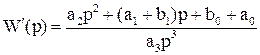В справедливости этого нетрудно убедиться на основании того, что характеристическое уравнение замкнутой системы 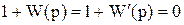сохраняет при этом свой вид:
.
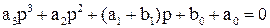