Задача 3.1
В неограниченном пласте, насыщенном за контуром нефтеносности водой с вязкостью примерно равной вязкости нефти µн = 1 мПа·с, пущены одновременно в эксплуатацию две добывающие скважины с равными дебитами q = 10-3 м3/с. Толщина пласта, его проницаемость и упругоемкость в нефтеносной части и за ее контуром одинаковы h = 12м, k = 0,5 ·10-12 м2, β = 5·10-10 Па-1. Расстояние между скважинами l = 300 м.
Определить насколько уменьшится давление по сравнению с начальным в пласте на середине расстояния между скважинами в начале координат спустя 29 суток (25·105 с) после пуска скважин в работу.
Решение.
Определим пьезопроводность пласта:
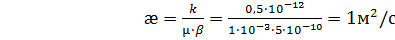 . (3.1)
. (3.1)
Если бы в бесконечном по протяженности пласте находился один точечный сток (добывающая скважина), то уменьшение давления определялось бы выражением:
 (3.3)
(3.3)
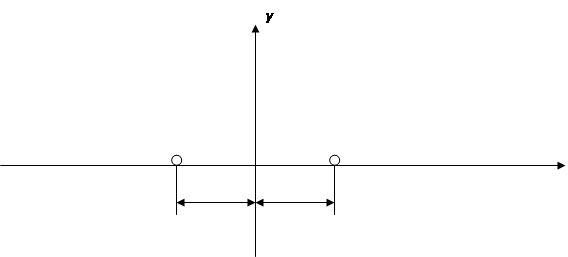
В нашем случае в бесконечном пласте имеются два точечных стока, причем каждый из них – на расстоянии l /2 от начала координат (рисунок 4.1).
 |
|  | ||||||
| |||||||
| |||||||
Рисунок 3.1 – Схема расположения двух скважин в бесконечном по протяженности пласте.
В этом случае, согласно принципу суперпозиции (принципу сложения фильтрационных потоков), из предыдущей формулы получаем:
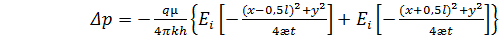 . (3.4)
. (3.4)
Из условия задачи для точки О имеем x=0 и y=0.
При этом предыдущее выражение примет вид:
 (3.5)
(3.5)
При t = 25·105 с. определим, что:
 .
.
При z= 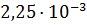 , значительно меньшем чем единица, можно воспользова- ться асимптотическим выражением для интегральной показательной функции:
, значительно меньшем чем единица, можно воспользова- ться асимптотическим выражением для интегральной показательной функции:
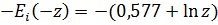 .
.
При z = 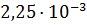 уменьшение давления посередине между добывающими скважинами через 29 суток работы равно:
уменьшение давления посередине между добывающими скважинами через 29 суток работы равно:

Соответственно при t = 58 суток (50·10-5 с) получим z = 1,12·10-3 и тогда:
|
|
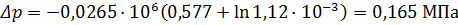 .
.
Задача 3.2
Нефтяная залежь, имеющая форму, которую можно приближенно представить в виде круга радиусом R = 500м, окружена бесконечно простирающейся плоской водоносной областью.
В момент времени t = 0 залежь начали разрабатывать с постоянным отбором жидкости q = 864 м3/сут = 10-2 м3/с (в пластовых условиях). В законтурной области вязкость в пластовых условиях µ = 1 мПа·с, проницаемость пласта k = 0,3·10-12 м2, толщина пласта h = 10 м, пьезопроводность пласта æ = 1 м2/с. Толщина пласта и его проницаемость в нефтеносной части и за ее контуром одинаковы h = 12 м, k = 0,5 ·10-12 м2.
Вычислить уменьшение давления на контуре нефтеносности ΔРконт в сравнении с начальным пластовым давлением через 58 и 116 суток после начала разработки залежи, считая залежь скважиной укрупненного радиуса (равного R = 500 м).
Для расчета уменьшения давления с течением времени на контуре нефтяной залежи используем простую аппроксимацию решений Ван Эвердингена и Херста, предложенную Ю. П. Желтовым. Имеем:
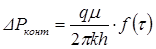 (3.6)
(3.6)
где 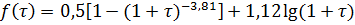 ;
;
и  .
.
При t = 5·106 c = 58 суток получаем:
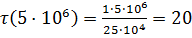 и
и 
А давление снизится на величину, равную:
 .
.
Через промежуток времени в 2 раза больше предыдущего находим:
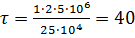 .
.
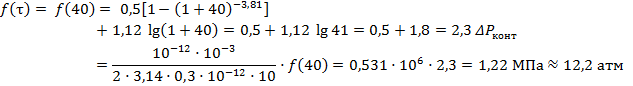
При t = 4 t1 = 4·5·106, τ = 80:
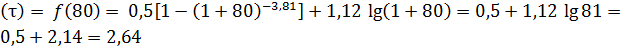
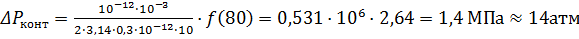 .
.
ВАРИАНТЫДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ К ЗАДАЧЕ 3.1
В неограниченном пласте, насыщенном за контуром нефтеносности водой с вязкостью примерно равной вязкости нефти µн = 1 мПа·с, пущены одновременно в эксплуатацию две добывающие скважины с равными дебитами q. Толщина пласта, его проницаемость и упругоемкость в нефтеносной части и за ее контуром одинаковы
|
|
| Варианты | |||||
| Толщина пласта h (м) | |||||
| Проницаемость k ( м2) | 0,54 ·10-12 | 0,58 ·10-12 | 0,63 ·10-12 | 0,45 ·10-12 | 0,56 ·10-12 |
| Упругоемкость β ( Па-1) | 5,4·10-10 | 6,1·10-10 | 4,7·10-10 | 5,3·10-10 | 5,8·10-10 |
| Расстояние между скважинами l (м) | |||||
| Дебит q (м3/с) | 9-3 | 12-3 | 15-3 | 18-3 | 10-3 |
Определить насколько уменьшится давление по сравнению с начальным в пласте на середине расстояния между скважинами в начале координат спустя 30, 92 и 270 суток после пуска скважин в работу.