Сложение скоростей
 Пусть по реке плывёт моторная лодка и нам известна её скорость
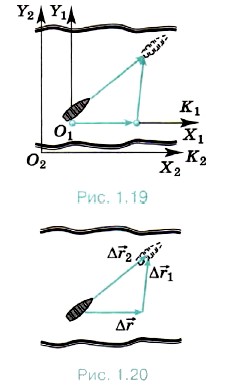
Пусть по реке плывёт моторная лодка и нам известна её скорость  1 относительно воды, точнее, относительно системы координат K1, движущейся вместе с водой (рис. 1.19).
1 относительно воды, точнее, относительно системы координат K1, движущейся вместе с водой (рис. 1.19).
Такую систему координат можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна ещё и скорость течения реки  относительно системы координат К2, связанной с берегом, т. е. скорость системы координат Кх относительно системы координат К2, то можно определить скорость
относительно системы координат К2, связанной с берегом, т. е. скорость системы координат Кх относительно системы координат К2, то можно определить скорость
лодки  2 относительно берега.
2 относительно берега.
За промежуток времени Δt перемещения лодки и мяча относительно берега равны Δ 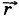 2 и Δ
2 и Δ 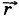 (рис. 1.20), а перемещение лодки относительно мяча равно Δ
(рис. 1.20), а перемещение лодки относительно мяча равно Δ 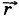 1. Из рисунка 1.20 видно, что.
1. Из рисунка 1.20 видно, что.
Δ 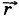 2 = Δ
2 = Δ 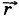 1 + Δ
1 + Δ 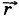 . (1)
. (1)
Разделив левую и правую части уравнения (1) на Δt, получим
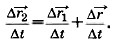
Учтём также, что отношения перемещений к интервалу времени равны скоростям. Поэтому
 2 =
2 =  1 +
1 +  . (2)
. (2)
Скорости складываются геометрически, как и все другие векторы. Уравнение (2) называют законом сложения скоростей.
Закон сложения скоростей Если тело движется относительно некоторой системы координат К1 со скоростью  и сама система К1 движется относительно другой системы координат К2 со скоростью и сама система К1 движется относительно другой системы координат К2 со скоростью  1, то скорость тела относительно второй системы равна геометрической сумме скоростей 1, то скорость тела относительно второй системы равна геометрической сумме скоростей  1 и 1 и  . .
|
Как и любое векторное уравнение, уравнение (2) представляет собой компактную запись скалярных уравнений, в данном случае — для сложения проекций скоростей движения на плоскости:
υ2x = υ1x + υx,
υ2y = υ1y + υy. (3)
Проекции скоростей складываются алгебраически.Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчёта, движущихся относительно друг друга.
|
|
 Часто скорость тела относительно неподвижной системы координат называют абсолютной скоростью, относительно подвижной системы координат — относительной, а скорость тела отсчёта, связанного с подвижной системой, относительно неподвижной — переносной скоростью. Тогда закон сложения скоростей имеет вид Часто скорость тела относительно неподвижной системы координат называют абсолютной скоростью, относительно подвижной системы координат — относительной, а скорость тела отсчёта, связанного с подвижной системой, относительно неподвижной — переносной скоростью. Тогда закон сложения скоростей имеет вид  a = a =  отн + отн +  пер. пер.
|
Примеры решения задач по теме «Сложение скоростей»
При решении задач на эту тему прежде всего надо грамотно выбрать тело отсчёта, с которым связать неподвижную систему координат. Затем выбрать тело отсчёта, движущееся относительно первого, и связать с ним подвижную систему координат. 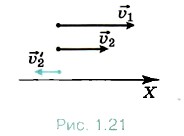 В этих двух системах рассмотреть движение тела и записать закон сложения скоростей.
В этих двух системах рассмотреть движение тела и записать закон сложения скоростей.
Задача 1. Два поезда движутся равномерно друг за другом. Скорость первого равна 80 км/ч, а скорость второго — 60 км/ч. Определите скорость второго поезда относительно первого.
Р е ш е н и е. Обозначим скорость первого поезда относительно земли через  1, а скорость второго поезда — через
1, а скорость второго поезда — через  2. Тогда согласно закону сложения скоростей (1.9)
2. Тогда согласно закону сложения скоростей (1.9)
 2 =
2 =  '2 +
'2 +  1,
1,
где  '2 — искомая скорость второго поезда относительно первого. Отсюда
'2 — искомая скорость второго поезда относительно первого. Отсюда
 '2 =
'2 =  2 -
2 -  1.
1.
Это сложение скоростей поясняется на рисунке 1.21. Из рисунка видно, что скорость второго поезда относительно первого направлена в сторону, противоположную направлению движения поездов, и второй поезд удаляется от первого. Проекция скорости  '2 на ось ОХ равна
'2 на ось ОХ равна
υ'2 = υ2 - υ1 = -20 км/ч.
Задача 2. Скорость течения реки υ = 1,5 м/с. Определите модуль скорости υ1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью υ2 = 2 м/с относительно его.
|
|
Р е ш е н и е. Согласно закону сложения скоростей (1.9)
 2 =
2 =  2 -
2 -  .
.
 Отсюда скорость катера относительно воды
Отсюда скорость катера относительно воды
 1 =
1 =  1 +
1 +  .
.
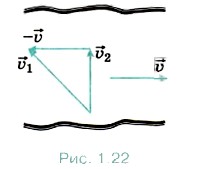
Векторное сложение скоростей  и
и  2 показано на рисунке 1.22.
2 показано на рисунке 1.22.
Так как полученный треугольник скоростей прямоугольный, то  1 = 2,5 м/с.
1 = 2,5 м/с.