Содержание
Ситуационная (практическая) задача № 1. 3
Ситуационная (практическая) задача № 2. 8
Тестовые задания. 13
Ситуационная (практическая) задача № 1
При штамповке шариков для подшипников происходят случайные отклонения диаметров шариков от номинала. При обследовании 25 шариков эти отклонения составили:
–0,530; –0,207; 0,025; –0,238; –0,132; 0,216; 0,087; 0,162; –0,462; –0,442;
–0,441; –0,163; –0,525; –1,136; 0,510; 0,316; 0,057; –0,402; –0,371; –0,351;
0,111;–0,161; 0,521; –0,551; 0,152.
Необходимо:
1. Определить исследуемый признак и его тип (дискретный или непрерывный).
2. В зависимости от типа признака построить полигон или гистограмму относительных частот.
3. На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4. Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.
5. Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.
6. Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.
7. С надежностью 0,95 проверить гипотезу о равенстве:
а) генеральной средней значению 0,7;
б) генеральной дисперсии значению 0,16
Решение:
1. Исследуемый признак непрерывный, так как может принимать любые значения на интервале и только точность измерения заставляет их округлять.
2. Ранжируем значения и проведем разбиение на k=1+3,32×lg(25)=5 интервалов.
Найдем шаг интервала:  (0,521-(-1,136))/5=0,331;
(0,521-(-1,136))/5=0,331;
| группа по величине отклонения, мм | число подшипников | относительная частота |
| от -1,136 до -0,805 | 0,04 | |
| от -0,805 до -0,474 | 0,12 | |
| от -0,474 до -0,143 | 0,4 | |
| от -0,143 до 0,188 | 0,28 | |
| от 0,188 до 0,521 | 0,16 | |
| итого |
Построим гистограмму:

3. При визуальном анализе гистограммы можем выдвинуть гипотезу о том, что признак распределен по нормальному закону.
4. Найдем выборочные характеристики изучаемого признака.
Расчетная таблица:
| i | xi | xi2 |
| -0,53 | 0,2809 | |
| -0,207 | 0,042849 | |
| 0,025 | 0,000625 | |
| -0,238 | 0,056644 | |
| -0,132 | 0,017424 | |
| 0,216 | 0,046656 | |
| 0,087 | 0,007569 | |
| 0,162 | 0,026244 | |
| -0,462 | 0,213444 | |
| -0,442 | 0,195364 | |
| -0,441 | 0,194481 | |
| -0,163 | 0,026569 | |
| -0,525 | 0,275625 | |
| -1,136 | 1,290496 | |
| 0,51 | 0,2601 | |
| 0,316 | 0,099856 | |
| 0,057 | 0,003249 | |
| -0,402 | 0,161604 | |
| -0,371 | 0,137641 | |
| -0,351 | 0,123201 | |
| 0,111 | 0,012321 | |
| -0,161 | 0,025921 | |
| 0,521 | 0,271441 | |
| -0,551 | 0,303601 | |
| 0,152 | 0,023104 | |
| Сумма | -3,955 | 4,096929 |
Среднее  -3,955/25=-0,1582
-3,955/25=-0,1582
 4,096929/25=0,1639
4,096929/25=0,1639
Дисперсия 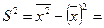 0,1639-(-0,1582)2=0,1389
0,1639-(-0,1582)2=0,1389
Среднее квадратическое (стандартное) отклонение
 0,1680,5=0,4099
0,1680,5=0,4099
5. Фактическое значение статистики χ2 определяется по формуле  , где pi – теоретическая вероятность попадания случайной величины в i-й интервал
, где pi – теоретическая вероятность попадания случайной величины в i-й интервал 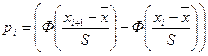 , она находится с помощью функции стандартного нормального распределения, значения которой Ф(х) найдем в таблице, xi- граница i-го интервала.
, она находится с помощью функции стандартного нормального распределения, значения которой Ф(х) найдем в таблице, xi- граница i-го интервала.
Объединим первый и второй интервалы.
Степень свободы теоретической статистики  равна k=5-2-1=2 т.к. пять интервалов определены выше и учитываем интервалы (-∞;-1,136) и (0,521;+∞) пустые интервалы объединим с соседними, уровень значимости α=0,05, теоретическое значение статистики
равна k=5-2-1=2 т.к. пять интервалов определены выше и учитываем интервалы (-∞;-1,136) и (0,521;+∞) пустые интервалы объединим с соседними, уровень значимости α=0,05, теоретическое значение статистики  5,99
5,99
Заполним расчетную таблицу:
| i | ni | интервал | xi | 
| 
| pi | npi | 
|
| -∞ | -∞ | |||||||
| (-∞;-0,805) | -0,805 | -1,74 | 0,0409 | 0,0409 | 1,023 | 0,001 | ||
| [-0,805;-0,474) | -0,474 | -0,85 | 0,1977 | 0,1568 | 3,92 | 0,216 | ||
| [-0,474;-0,143) | -0,143 | 0,04 | 0,5160 | 0,3183 | 7,958 | 0,524 | ||
| [-0,143;0,188) | 0,188 | 0,93 | 0,8238 | 0,3078 | 7,695 | 0,063 | ||
| [0,188;+∞) | +∞ | +∞ | 1,0000 | 0,1762 | 4,405 | 0,037 | ||
| Итого | 25,00 | 0,841 |
т.к.  значит гипотеза о нормальном распределении величины отклонения согласуется с опытными данными;
значит гипотеза о нормальном распределении величины отклонения согласуется с опытными данными;
6. Для генерального среднего  с вероятностью γ=0,95:
с вероятностью γ=0,95:
Квантиль Стьюдента 
Предельная ошибка выборки  0,1819
0,1819
Доверительный интервал  :
:
-0,1582-0,1819  -0,1582+0,1819
-0,1582+0,1819
 [-0,3401; 0,0237]
[-0,3401; 0,0237]
Для генеральной дисперсии 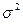 :
:
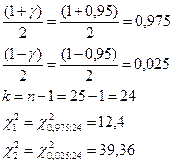
Доверительный интервал  :
:
25x0,1389/12,4<  <25x0,1389/39,36
<25x0,1389/39,36
 [0,088; 0,28]
[0,088; 0,28]
Итак с надежностью γ=0,95 лежит в интервале от -0,3401 до 0,0237 мм, а дисперсия заключена в границах от 0,088 до 0,28.
7. С надежностью 0,95 проверим гипотезу о равенстве:
а) Гипотеза Н0 :генеральная средняя равна значению а0=0,7, при неизвестной дисперсии.
Найдем значение t-статистики

| -0,1582-0,7 | =11,281 |
0,3727/ 
|
 <11,281
<11,281 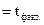 , значит, с надежностью 0,95 выдвинутая гипотеза не подтверждается опытными данными.
, значит, с надежностью 0,95 выдвинутая гипотеза не подтверждается опытными данными.
б) Гипотеза Н0 : генеральная дисперсия равна значению  =0,16, при неизвестном среднем.
=0,16, при неизвестном среднем.
Найдем значение «Хи квадрат»-статистики
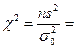
| 25x0,1389 | =21,703 |
| 0,16 |

 следовательно гипотеза Н0 подтвердилась (не опровергнута) опытными данными.
следовательно гипотеза Н0 подтвердилась (не опровергнута) опытными данными.