Содержание задачи.
Понтон плавает таким образом, что один из его торцов полностью выступает из воды, а другой – касается ее поверхности своей верхней кромкой (рис 1).
Определить объемное водоизмещение понтона и силы избыточного гидростатического давления на погруженный торец Rт и на подводную часть цилиндрической поверхности Rц.
2. Исходные данные и принятые положения:
Длинна понтона, L, м 16
Диаметр понтона, D, м 4,5
Положение понтона в воде см. рис.1
Плотность воды, ρ, m/м3 1,025
Ускорение свободного падения, g, м/сек2 9,81
В работе принята декартова система координат с началом на свободной поверхности (см. рис. 1). При этом оси X и Z лежат в продольно-вертикальной плоскости симметрии подводной части понтона (в диаметральной плоскости): ось X горизонтальна, а ось Z направлена вертикально. Ось Y перпендикулярна диаметральной плоскости (ДП).
Ось симметрии понтона обозначена как ось Х1, а перпендикуляр к ней в ДП – как ост Z1 (см. рис. 1).

Рис. 1
3.
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.180101.65.07 |
Объемное водоизмещение (объем подводной части) понтона V при описании в. п. 1 его посадке будет равно половине полного объема понтона Vп, т.е.
 (1.1)
(1.1)
или
 . (1.2)
. (1.2)
Определить силы избыточных давлений действующей на всю смоченную поверхность понтона.
Искомая сила 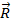 в общем случае может быть выражена через ее проекции в виде равенства:
в общем случае может быть выражена через ее проекции в виде равенства:
 (1.3)
(1.3)
В (1.3):
 (1.4)
(1.4)
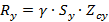 (1.5)
(1.5)
 (1.6)
(1.6)
где Sx b Sy – проекции ориентированной смоченной поверхности понтона 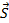 , соответственно, на координатные плоскости yOx и xOz;
, соответственно, на координатные плоскости yOx и xOz;
Zсх и Zcy – аппликаты центров тяжести проекций Sx и Sy;
Vтд – объем тела давления смоченной поверхности, равный в нашем случае объемному водоизмещению V;
γ= ρ∙g – удельный вес воды;
g= 9,81 м/с2 – ускорение свободного падения.
Замкнем рассматриваемую смоченную поверхность свободной поверхностью 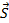 n, лежащей внутри граничного контура поверхностью
n, лежащей внутри граничного контура поверхностью 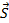 (см. рис. 1).
(см. рис. 1).
Проекции образованной таким образом замкнутой ориентированной поверхности
 n (1.7)
n (1.7)
на любую из координат плоскостей равны нулю /3, с. 433/, т.е.
 (1.8)
(1.8)
и
 . (1.9)
. (1.9)
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.180101.65.07 |
 n на вертикальные плоскости yOz и xOz имеют форму прямых линий, их площади Snx и Sny равны нулю и, в соответствии с уравнениями (1.8) и (1.9),
n на вертикальные плоскости yOz и xOz имеют форму прямых линий, их площади Snx и Sny равны нулю и, в соответствии с уравнениями (1.8) и (1.9),
Sx = ∑x = 0 (1.10)
и
Sy = ∑y = 0 (1.11)
Подставляя полученные значения Sx и Sy в формулы (1.4) и (1.5), получим
Rx = Ry = 0. (1.12)
Таким образом, результирующая гидростатическая сила 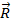 равна по модулю величине
равна по модулю величине
R = Rz = γV = 1277 кН, (1.13)
направлена вертикально вверх и, ввиду симметрии смоченной поверхности относительно диаметральной плоскости, лежит в ДП.
Определение сил избыточных давлений на торце и на боковой цилиндрической поверхности.
При определении сил учтем их ориентацию и то обстоятельство, что в сумме они составляют силу 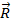 .
.
Ввиду симметрии торца и погруженной части боковой цилиндрической поверхности относительно ДП силы 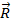 т и
т и 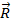 ц должны лежать в диаметральной плоскости понтона. В ДП находится также результирующая сила
ц должны лежать в диаметральной плоскости понтона. В ДП находится также результирующая сила 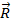 .
.
Сила 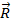 т направлена перпендикулярно торцу, т.е. вдоль симметрии понтона Х1.
т направлена перпендикулярно торцу, т.е. вдоль симметрии понтона Х1.
В свою очередь, составляющие силы 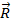 ц на всех участках цилиндрической поверхности направлены по нормали к этой поверхности и, значит, параллельны торцу. Поэтому результирующая сила
ц на всех участках цилиндрической поверхности направлены по нормали к этой поверхности и, значит, параллельны торцу. Поэтому результирующая сила 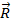 ц также параллельна торцу и, поскольку принадлежит ДП, должна быть параллельна оси Z1.
ц также параллельна торцу и, поскольку принадлежит ДП, должна быть параллельна оси Z1.
Таким образом, силы 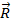 т и
т и 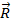 ц взаимно перпендикулярны и их численные значения могут быть определены по формулам
ц взаимно перпендикулярны и их численные значения могут быть определены по формулам
Rт = R∙sinα (1.14)
и
Rц = R∙cosα, (1.15)
где α – угол между осями Ох и Ох1,
sin α =  = 0,271 (1.16)
= 0,271 (1.16)
и
cos α =  = 0,963 (1.17)
= 0,963 (1.17)
Подставляя в (1.14) и (1.15) значения R, sin α и cos α по (1.13), и (1.16) и (1.17), получим искомые значения сил на торце и на цилиндрической поверхности
| Изм. |
| Лист |
| № документа |
| Подпись |
| Дата |
| Лист |
| КР.ГМХ.180101.65.07 |
и
Rц = 1195 кН. (1.19)