"Численные методы"
1. Пусть в приближенном значении а=16,395 все цифры верны. Округлите а до сотых. Найти погрешность округления и полную погрешность.
2. Округляя число х=1,1426 до 4-х значащих цифр, определить абсолютную и относительную погрешности полученных приближений. Учесть, что все цифры верны.
3. Число х=1,1426, все цифры которого верны, округлить до 4-х значащих цифр. Для получения результата х1 вычислить границы абсолютной погрешности. В записи числа х1 указать количество верных цифр.
4. Приближенное значение х=24,6035 имеет относительную погрешность d(x)=0,2 %. Найдите ∆(x).
5. Округлите числа π =3,1415926... и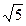 
=0,70710678... до четырех значащих цифр, а затем найдите абсолютные погрешности результатов с одной и двумя значащими цифрами.
6. Определить относительную погрешность приближенного числа b = 2,3254 по ее абсолютной погрешности Δb = 0,01, предварительно округлив число b до верных знаков.
7. Даны числа a = 23,37 и b = 23,13 с абсолютными погрешностями Δa=Δb=0,21. Оценить погрешность их разности c = a – b.
8. Найти относительную погрешность приближенного числа a = 4231,92 по ее абсолютной погрешности Δa = 2, предварительно округлив число a до верных знаков.
9. Длина и ширина аудитории, измеренные с точностью до
1 дм, равны a = 12,49 м и b = 5,12 м. Оценить абсолютную погрешность в определении площади аудитории S = a·b = 63,9488 м2.
10. Найти минимум функции f(x)=2x2-12x методом равномерного поиска.
11. Найти минимум функции f(x)=2x2-12x методом деления интервала пополам.
12. Найти минимум функции f(x)=2x2-12x методом дихотомии.
13. Найти минимум функции f(x)=2x2-12x методом золотого сечения.
14. Найдите максимум функции f(x)=2x4–x+5 методом дихотомии.
15. Найдите максимум функции f(x)=2x4–x+5 методом золотого сечения.
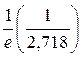
16. Найти значение с помощью многочлена Лагранжа, если задана таблица
| X | 2,66 | 2,70 | 2,7 |
| F(x) | 0,3759 | 0,3731 | 0,3704 |
17. Выясните, будет ли функция y=x2+x интерполирующей для данной табличной функции:
| x | -2 | |||||
| f(x) |
18. Дана таблица значений функции y=ex. Постройте интерполяционный многочлен Лагранжа второй степени.
| x | 1.5 | 1.6 | 1.7 |
| ex | 4.48 | 4.95 | 5.47 |
19. По таблице постройте интерполяционный многочлен Лагранжа:
| x | -1 | |||
| y |
20. Написать интерполяционный полином Лагранжа для функции f(x), которая представлена четырьмя своими значениями:
f(0) = –0,5; f(0,1) = 0; f(0,3) = 0,2 и f(0,5) = 1.
21. По таблице постройте первый интерполяционный многочлен Ньютона:
| x | -1 | |||
| y |
22. По таблице постройте второй интерполяционный многочлен Ньютона:
| x | -1 | |||
| y |
23. По таблице постройте первый многочлен Ньютона вычислите значение функции в точке x=1,57.
| x | 1.5 | 1.6 | 1.7 |
| ex | 4.48 | 4.95 | 5.47 |
24. По таблице постройте второй многочлен Ньютона вычислите значение функции в точке x=1,57.
| x | 1.5 | 1.6 | 1.7 |
| ex | 4.48 | 4.95 | 5.47 |
25. В результате экспериментов получена следующая таблица:
| x | -0.2 | 0.5 | 1.2 | 1.5 | 2.5 | 2.9 | 3.3 | 4.5 | ||||
| f(x) | -0.3 | 0.6 | 0.9 | 1.1 | 1.4 | 0.8 | 0.5 | -0.1 | -0.3 | -0.8 | -0.4 | 0.1 |
Начертите график функции по данным таблицы и подберите функцию, с помощью которой можно приблизить функцию f.
26. Составьте таблицу значений функции y=6lg(3x) на отрезке [1; 5] с шагом h=0,6. В значениях функции сохраняйте три знака в дробной части. Вычислите значение функции в точке x=3,52. Вычисления проведите по формуле Ньютона.
27. По заданной таблице значений составить линейные сплайны.
| Функция | X1 | X2 | X3 |
| x | 0.5 | 0.6 | 0.7 |
| sin x | 0.47943 | 0.56464 | 0.64422 |
28. По заданной таблице значений составить параболические сплайны.
| Функция | X1 | X2 | X3 |
| x | 0.5 | 0.6 | 0.7 |
| cos x | 0.87758 | 0.82534 | 0.76484 |
29. По заданной таблице значений составить кубические сплайны.
| Функция | X1 | X2 | X3 |
| x | 0.5 | 0.6 | 0.7 |
| tg x | 0.54630 | 0.68414 | 0.84229 |
30. Пусть дан фрагмент таблицы значений функции:
| x | -1 | ||
| y | 1.5 | 0.5 | 2.5 |
Требуется построить параболический сплайн.
31. Составьте таблицу значений, используя исходные данные:
Найдите полином второй степени, аппроксимирующий эту таблицу.
32. Найдите приближенную функцию по методу наименьших квадратов для функции, заданной таблицей своих значений:
| x | -3 | -1 | |||
| y | -4 | -0.8 | 1.6 | 2.3 | 1.5 |
33. Произвести отделение корней уравнения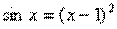 
на интервале [0.1; 5.0], уточнить их значения до 
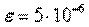методом половинного деления.
34. Произвести отделение корней уравнения 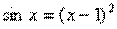на интервале [0.1; 5.0], уточнить их значения до 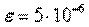методом простой итерации.
35. Произвести отделение корней уравнения 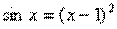на интервале [0.1; 5.0], уточнить их значения до 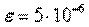методом касательных.
36. Отделите корни уравнения 3cos x=x+1.
37. Уточните корень уравнения x–sinx–0,25=0 на отрезке [1,1;1,2] с точностью до 0,001 методом простой итерации.
38. Уточните корень уравнения x–sinx–0,25=0 на отрезке [1,1;1,2] с точностью до 0,001 методом дихотомии.
39. Убедитесь в применимости метода хорд для уравнения
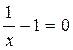на отрезке [0,5;2] изоляции его корня и вычислите с тремя значащими цифрами приближения x1, x2.
40. Корень уравнения 1+x–x4=0 изолирован на отрезке [1;2]. Вычислите приближения x1, x2 методом касательных.
41. Дано уравнение x3 + x2 -1 =0. Привести данное уравнение к виду, при котором выполняются достаточные условия сходимости для метода простой итерации на отрезке [0; 1].
42. Найти методом деления отрезка пополам корень уравнения
cos x − x = 0 на интервале [0,7; 0,8] с точностью ε = 10-2.
43. Дано уравнение x2 – 100x + 1 =0. Привести данное уравнение к виду, при котором выполняются достаточные условия сходимости для метода простой итерации на отрезке [0; 1].
44. Дано нелинейное уравнение sin x − 0,5x = 0. Определить методом деления отрезка пополам корень данного уравнения на интервале [1,7; 2] с точностью ε = 10-2.
45. Решите систему уравнений методом итераций
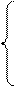12x1 + x2 - 5x3 = 21,
4x1 - 5x2 + x3 = -1,
-3x1 + 4x2 + 3x3 = 5.
46. Решите систему уравнений методом Зейделя
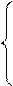12x1 + x2 - 5x3 = 21,
4x1 - 5x2 + x3 = -1,
-3x1 + 4x2 + 3x3 = 5.
47. 
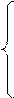Решите систему линейных уравнений методом итераций:
3x1 + 2x2 + x3 = 4,
x1 + x2 - x3 = 1,
x1 - 2x2 + x3 = 3.
48. 
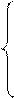Решите систему линейных уравнений методом Зейделя:
3x1 + 2x2 + x3 = 4,
x1 + x2 - x3 = 1,
x1 - 2x2 + x3 = 3.
49. Решите систему линейных уравнений методом Зейделя.
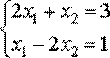
50. Вычислить интеграл 
с помощью формулы правых прямоугольников
51. Вычислить интеграл с помощью формулы левых прямоугольников
52. Вычислить интеграл с помощью формулы центральных прямоугольников
53. Вычислить интеграл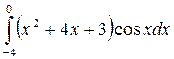 
с помощью формулы трапеций
54. Вычислить интеграл 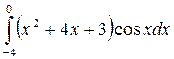с помощью формулы Симсона
55. 
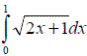Найдите приближенное значение интеграла по формуле трапеций.
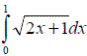
56. Найдите приближенное значение интеграла по формуле Симсона.
57. 
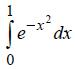Оценить погрешность вычисления R интеграла
по формуле трапеций при равномерном шаге h = 0,1.
58. 
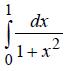Определить величину шага h по оценке остаточного члена
для вычисления интеграла по формуле трапеций с точностью до 10-2.
59. 
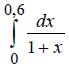Оценить погрешность вычисления интеграла по формуле Симпсона при равномерном шаге h = 0,1.
60. 
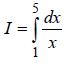Вычислить по формуле трапеций интеграл при
n = 4 и оценить остаточный член.
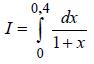
61. Вычислить приближенно интеграла по
формуле трапеций при n = 4 и оценить остаточный член.
62. Дано дифференциальное уравнение y'=2xy. Найдите методом Эйлера на отрезке [0;1] с шагом h=0,2 численное решение задачи Коши с начальным условием y(0)=1. Определите погрешности yi методом Рунге.
63. Дано дифференциальное уравнение y'=2xy. Найдите методом серединных точек на отрезке [0;1] с шагом h=0,2 численное решение задачи Коши с начальным условием y(0)=1.
64. Дано дифференциальное уравнение y'=2xy. Найдите методом Рунге-Кутта на отрезке [0;1] с шагом h=0,2 численное решение задачи Коши с начальным условием y(0)=1.
65. Дано уравнение y"=3x+y' и начальные условия y(1)=1, y'(1)=0. Применяя метод Эйлера, найдите численное решение задачи Коши на отрезке [1;2] с шагом h=0,5.
66. Выполнить 1 шаг длины 0.4 с использованием усовершенствованного метода Эйлера для решения задачи Коши:
67. Применяя метод Эйлера, найти решение задачи Коши:
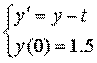в трех последовательных точках 
, 
, 
.
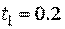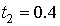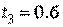68. Применяя метод Эйлера, численно решить дифференциальное уравнение y′ = 0,5 xy с начальным условием y(0) = 1 на отрезке [0; 1] с шагом h = 0,2.
69. Применяя метод Эйлера, найти решение обыкновенного дифференциального уравнения y΄= y – 2x/y на интервале [0; 1] с начальным условием y(0) = 1, выбрав шаг h = 0,2.
70. Методом Рунге-Кутта найти решение на отрезке [0;0.3] дифференциального уравнения y’=-xy/(1+x2) при начальном условии y(0)=2 с шагом h=0.05.