Задача Д1
Груз Dмассой  получив в точке A начальную скорость
получив в точке A начальную скорость  , движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д 1.0 —Д 1.9, табл. Д1).
, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д 1.0 —Д 1.9, табл. Д1).
На участке ABна груз, кроме силы тяжести, действуют постоянная сила  (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды  , зависящая от скорости
, зависящая от скорости  груза (направлена против движения); трением груза о трубу на участке ABпренебречь.
груза (направлена против движения); трением груза о трубу на участке ABпренебречь.
В точке Bгруз, не изменяя своей скорости, переходит на участок BCтрубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу  ) и переменная сила
) и переменная сила  , проекция которой
, проекция которой  на ось
на ось  задана в таблице.
задана в таблице.
Считая груз материальной точкой и зная расстояние AB= l или время  движения груза от точки A до точки B,найти закон движения груза на участкеBC, т. е.
движения груза от точки A до точки B,найти закон движения груза на участкеBC, т. е.  ,где x = BD.
,где x = BD.
Указания. Задача Д1 — на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке  , учтя начальные условия. Затем, зная время движения груза на участке
, учтя начальные условия. Затем, зная время движения груза на участке  или длину этого участка, определить скорость груза в точке
или длину этого участка, определить скорость груза в точке  . Эта скорость будет начальной для движения груза на участке
. Эта скорость будет начальной для движения груза на участке  . После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке
. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке  тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке
тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке  , и полагая в этот момент
, и полагая в этот момент  . При интегрировании уравнения движения на участке
. При интегрировании уравнения движения на участке  в случае, когда задана длина
в случае, когда задана длина  участка, целесообразно перейти к переменному
участка, целесообразно перейти к переменному  , учтя, что
, учтя, что

Таблица Д1
| Номер условия | m, кг | v о, м/с | Q, H | R,H | l, м | t1, c | F x, H |
| 8,3 | 0,4v | - | 2,5 | 18 sin (4t) | |||
| 2,4 | 11,4 | 0,8v2 | 1,5 | - | 3t | ||
| 4,5 | 0,5v | - | 25 sin(2t) | ||||
| 18,3 | 0,6v2 | - | -4 cos(2t) | ||||
| 1,6 | 2,9 | 0,4v | - | 3 cos(4t) | |||
| 4,5 | 0,5v2 | - | -12sin(2t) | ||||
| 1,8 | 17,6 | 0,3v | - | 33t2 | |||
| 22,1 | 0,8v2 | 2,5 | - | - 6 cos (4t) | |||
| 15,4 | 0,5v | - | 12 cos (2t) | ||||
| 4,8 | 0,9 | 0,2v2 | - | -6,5 sin (4t) |

Рис. Д1.0 Рис. Д1.1

Рис. Д1.2 Рис. Д1.3

Рис. Д1.4 Рис. Д1.5

Рис. Д1.6 Рис. Д1.7
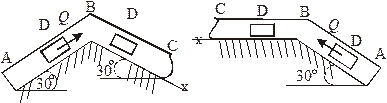
Рис. Д1.8 Рис. Д1.9
Задача Д2
Механическая система состоит из прямоугольной вертикальной плиты 1 массы  кг, движущейся вдоль горизонтальных направляющих, и груза D массы
кг, движущейся вдоль горизонтальных направляющих, и груза D массы  кг (рис. Д2.0 — Д2.9, табл. Д2). В момент времени
кг (рис. Д2.0 — Д2.9, табл. Д2). В момент времени  , когда скорость плиты
, когда скорость плиты  м/с, груз под действием внутренних сил начинает двигаться по желобу плиты.
м/с, груз под действием внутренних сил начинает двигаться по желобу плиты.
На рис. Д2.0 – Д2.3 желоб КЕпрямолинейный и при движении груза расстояние s = ADизменяется по закону  ,ана рис. Д2.4 – Д2.9 желоб – окружность радиуса R =0,8 м и при движении груза угол
,ана рис. Д2.4 – Д2.9 желоб – окружность радиуса R =0,8 м и при движении груза угол  изменяется по закону
изменяется по закону 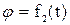 . В табл. Д2 эти зависимости даны отдельно для рис. Д2.0 и Д2.1, для рис. Д2.2 и Д2.3 и т.д., где s выражено в метрах,
. В табл. Д2 эти зависимости даны отдельно для рис. Д2.0 и Д2.1, для рис. Д2.2 и Д2.3 и т.д., где s выражено в метрах,  – в радианах, t – в секундах.
– в радианах, t – в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость  , т.е. скорость плиты как функцию времени.
, т.е. скорость плиты как функцию времени.
Указания. Задача Д2 – на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.

Рис. Д2.0 Рис. Д2.1 Рис. Д2.2
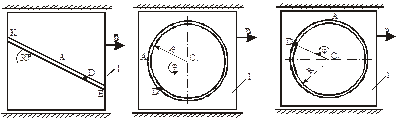
Рис. Д2.3 Рис. Д2.4 Рис. Д2.5
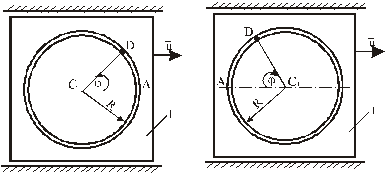
Рис. Д2.6 Рис. Д2.7
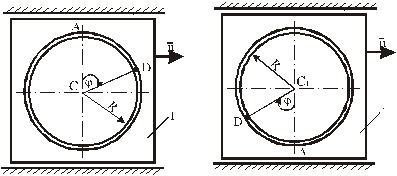
Рис. Д2.8 Рис. Д2.9
Таблица Д2
| Номер условия | 
| 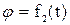
| ||
| pис. Д2.0, Д2.1 | рис. Д2.2, Д2.3 | рис. Д2.4 – Д2.6 | pис. Д2.7 – Д2.9 | |
0,4sin( t2) t2)
| 0,4(6t2-2) | 2  (3-2t2)/3 (3-2t2)/3
| 4  (2t2-1) (2t2-1)
| |
1,6cos( t/2) t/2)
| 0,8sin( t2/2) t2/2)
| 4  (1-3t2)/4 (1-3t2)/4
| 2  (1-4t2)/3 (1-4t2)/3
| |
| 0,9(2t2-1) | 1,2cos( t) t)
| 2  (t2-3)/6 (t2-3)/6
| 4  (3+4t2)/6 (3+4t2)/6
| |
2,4sin( t2/3) t2/3)
| 2,3sin( t2/6) t2/6)
| 4  (2-t2) (2-t2)
| 2  (t2+1)/2 (t2+1)/2
| |
1,5cos( t/6) t/6)
| 0,6cos( t/3) t/3)
| 2  (1+2t2)/6 (1+2t2)/6
| 4  (1-5t2)/4 (1-5t2)/4
| |
2,6sin( t2/4) t2/4)
| 3,7(3-4t2) | 4  (5t2+1)/4 (5t2+1)/4
| 2  (t2-4)/3 (t2-4)/3
| |
| 1,8(2-3t2) | 4,8sin( t2/3) t2/3)
| 2  (t2-2)/2 (t2-2)/2
| 4  t2/4 t2/4
| |
6,6cos( t/3) t/3)
| 2,9cos( t/4) t/4)
| 4  (3+t2)/3 (3+t2)/3
| 2  (3t2-1)/6 (3t2-1)/6
| |
1,8sin( t2/6) t2/6)
| 7,2sin( t2) t2)
| 2  t2/2 t2/2
| 4  (t2+3)/4 (t2+3)/4
| |
0,9cos( t/4) t/4)
| 1,8cos( t/6) t/6)
| 4(t2+2)/6 | 2  (2- t2)/4 (2- t2)/4
|
Задача Д3
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R 3=0,3 м, r 3=0,1 м и радиусом инерции относительно оси вращения  =0,2 м, блока 4 радиуса R 4=0,2 м и катка (или подвижного блока) 5 (рис. Д3.0 – Д3.9, табл. Д3); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f =0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
=0,2 м, блока 4 радиуса R 4=0,2 м и катка (или подвижного блока) 5 (рис. Д3.0 – Д3.9, табл. Д3); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f =0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f (s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s 1=0,2 м. Искомая величина указана в графе «Найти» таблицы, где обозначено: V 1, V 2, Vc5 – скорости грузов 1, 2 ицентра масс тела 5соответственно,  и
и  – угловые скорости тел 3 и 4.
– угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5на рис. Д3.2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2,если m 2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д3 – на применение теоремы об изменении кинетической энергии системы. При решении задачи следует учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
| Номер условия | m 1, кг | m 2, кг | m 3, кг | m 4, кг | m 5, кг | c, Н/м | M, Н×м | F = f (s), Н | Найти |
| 1,2 | 80(4+5s) | 
| |||||||
| 0,8 | 50(8+3s) | 
| |||||||
| 1,4 | 60(6+5s) | 
| |||||||
| 1,8 | 80(5+6s) | 
| |||||||
| 1,2 | 40(9+4s) | 
| |||||||
| 1,6 | 50(7+8s) | 
| |||||||
| 0,8 | 40(8+9s) | 
| |||||||
| 1,5 | 60(8+5s) | 
| |||||||
| 1,4 | 50(9+2s) | 
| |||||||
| 1,6 | 80(6+7s) | 
|
Таблица Д3

Рис. Д3.0 Рис. Д3.1

Рис. Д3.2 Рис. Д3.3

Рис. Д3.4 Рис. Д3.5

Рис. Д3.6 Рис. Д3.7

Рис. Д3.8 Рис. Д3.9
Сложное движение материальной точки
Задача К4
Прямоугольная пластина (рис. К4.0 – К4.4) или круглая пластина радиуса r =60 см (рис. К4.5 – К4.9) вращается вокруг неподвижной оси по закону  , заданному в табл. К4. Положительное направление отсчета угла
, заданному в табл. К4. Положительное направление отсчета угла  показано на рисунках дуговой стрелкой. На рис. К4.0, К4.1, К4.2, К4.5, К4.6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. К4.3, К4.4, К4.7, К4.8, К4.9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
показано на рисунках дуговой стрелкой. На рис. К4.0, К4.1, К4.2, К4.5, К4.6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. К4.3, К4.4, К4.7, К4.8, К4.9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой Вd (рис. К4.0 – К4.4) или по окружности радиуса R (рис. К4.5 – К4.9) движется точка М; закон ее относительного движения, т.е. зависимость s =АМ = f2(t) (s –в сантиметрах, t – в секундах), задан в таблице отдельно для рис. К4.0 – К4.4, и для рис. К4.5 – К4.9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s =АМ > 0 (при s < 0 точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t 1 =1 с.
Указания. Задача К4 – на сложное движение точки. Для ее решения следует воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, необходимо по условиям задачи определить, где находится точка М на пластине в момент времени t 1 =1 с, и изобразить точку именно в этом положении (а не в произвольном, как показано на рисунках к задаче).
В случаях, относящихся к рис. К4.5 – К4.9, при решении задачи не подставлять числовое значение R, пока не будут определены положение точки М в момент времени t 1 =1 с и угол между радиусами СМ и СА в этот момент.

Рис. К4.0 Рис. К4.1 Рис. К4.2
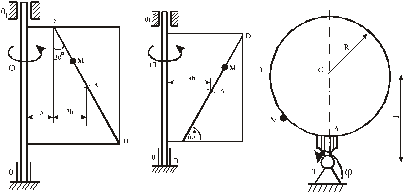
Рис. К4.3 Рис. К4.4 Рис. К4.5

Рис. К4.6 Рис. К4.7

Рис. К4.8 Рис. К4.9
Таблица К4
| Номер условия | Для всех рисунков  ) )
| Для рис. К4.0-К4.4 | Для рис. К4.5-К4.9 | ||
| b, см | s =АМ = f 2(t) | l | s =АМ = f 2(t) | ||
| 4(t 2 – t) | 50(3 t – t 2)-64 | R |  (4 t 2 – 2 t 3) (4 t 2 – 2 t 3)
| ||
| 3 t 2 -8 t | 40(3 t 2 – t 4) -32 | 4/3 R |  (2 t 2 – t 3) (2 t 2 – t 3)
| ||
| 6 t 3 – 12 t 2 | 80(t 2 – t)+40 | R |  (2 t 2 – 1) (2 t 2 – 1)
| ||
| t 2 –2 t 3 | 60(t 4 –3 t 2)+56 | R |  (3 t – t 2) (3 t – t 2)
| ||
| 10 t 2 – 5 t 3 | 80(2 t 2 – t 3)-48 | R |  (t 3 – 2 t) (t 3 – 2 t)
| ||
| 2(t 2 – t) | 60 (t 3 – 2 t 2) | R | 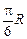 (t 3 – 2 t) (t 3 – 2 t)
| ||
| 5 t – 4 t 2 | 40(t 2 –3 t) + 32 | 3/4R |  (t 3 – 2 t 2) (t 3 – 2 t 2)
| ||
| 15 t – 3 t 3 | 60(t – t 3) + 24 | R | 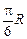 (t – 5 t 2) (t – 5 t 2)
| ||
| 2 t 3 – 11 t | 50 (t 3 – t) - 30 | R |  (3 t 2 – t) (3 t 2 – t)
| ||
| 6 t 2 – 3 t 3 | 40(t – 2 t 3) - 40 | 4/3 R |  (t – 2 t 2) (t – 2 t 2)
|
Ответ: V абс =234 см/с; a абс =634,8 см/с2.