Главной целью логистики является обеспечение конкурентоспособных позиций организации бизнеса на рынке. Этого логистика добивается посредством управления потоковыми процессами на основе следующих правил: доставка с минимальными издержками необходимой конкретному покупателю продукции соответствующего качества и соответствующего количества в нужное место и в нужное время (семь правил логистики).
Необходимо отметить, что представленные правила являются выражением идеального случая, к которому следует стремиться.
Логистические цели достаточно универсальны и вполне органично вписываются в стратегические и тактические цели хозяйственной организации. Таким образом происходит интеграция целей горизонтальная (взаимоувязка целей в каждой отдельно взятой функциональной сфере) и вертикальная (взаимоувязка целей по уровням управления). Например, цель: максимальная загрузка существующих складских мощностей при минимальных затратах на складирование.
В логистической системе как при горизонтальной, так и при вертикальной интеграции важны постоянное взаимодействие и наличие обратных связей между функциональными сферами и уровнями управления. Это является важнейшим определяющим условием эффективности процессов выработки и реализации управленческих и исполнительных решений.
Для практической реализации целей логистики необходимо найти адекватные решения ряда соответствующих задач, которые по степени значимости разделяются на две группы: глобальные и частные (локальные) задачи.
К глобальным задачам логистики относятся следующие:
ü создание комплексных, интегрированных систем материальных, информационных, а по возможности и других сопутствующих потоков;
|
|
ü стратегическое согласование, планирование и контроль за использованием логистических мощностей сфер производства и обращения;
ü достижение высокой системной гибкости;
ü постоянное совершенствование логистической концепции в рамках избранной стратегии в рыночной среде.
При решении глобальных задач очень важен временной компонент. Дело в том, что внешняя среда меняется достаточно быстро, поэтому, если решение глобальной задачи происходит медленнее, чем происходят изменения во внешней среде, результат решения будет отрицательным.
Частные задачи в логистике имеют локальный характер, они более динамичны и разнообразны:
Ø максимальное сокращение времени хранения продукции;
Ø сокращение времени перевозок;
Ø рациональное распределение транспортных средств;
Ø быстрая реакция на требования потребителей;
Ø оперативная обработка и выдача информации и т. п.
Решение такой частной задачи, как сокращение времени перевозок в условиях автомобильных пробок (сегодня в условиях жесткой конкуренции многие компании начинают вести счет времени на часы и минуты), для многих организаций налицо — переход на ночную развозку.
Решения глобальных и локальных задач должны находиться в рамках общих задач логистической системы, к которым относят следующие:
· осуществление сквозного контроля за потоковыми процессами;
· разработка и совершенствование способов управления материальными потоками;
§ многовариантное прогнозирование развития событий и т. п.;
|
|
§ стандартизация требований к качеству логистических операций;
§ выявление несбалансированности между потребностями рынка и возможностями логистической системы;
§ выявление центров возникновения потерь ресурсов;
§ оптимизация технической и технологической структуры организации и т. п.
Задачи.
Задача назначения. Вариант №1
| Вариант 1 | |||||
| А | B | C | D | E | |
1.Осуществляем приведение матрицы по строчкам. В каждой строке ищем минимальный элемент и вычитаем его значение из всех «клеток» строки.
| А | B | C | D | E | ||
| А | B | C | D | E | |
2.Аналогичным образом осуществляем приведение матрицы по столбцам.
| А | B | C | D | E | |||||
| А | B | C | D | E | |
|
|
Предварительные трудозатраты на выполнение комплекса работ равны
T=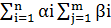 
=9+2=11
3.В «клетках» с нулями пытаемся разместить n ладьей так, чтобы они «не били» друг друга.
4. Пока мы видим, что сделать это невозможно, значит, проводим эквивалентное преобразование через все нолики проводим минимальное количество пересекающихся прямых.
Среди открытых клеток ищем минимальный элемент.
| А | B | C | D | E | |
 1
|  0
|  5
| |||
 0
| |||||
 0
| |||||
 7
| |||||
| 0
|
=1
Значение минимального элемента дополняется к общим трудозатратам
T1=T+1=11+1=12
Значение вычитается из открытых клеток, прибавляется к клеткам на пересечении, остальное без изменений.
| А | B | C | D | E | |
| 1
|  0
| ||||
| 5
| 0 | ||||
| 0
| |||||
| 7
| 0 | ||||
 0
|
Возвращаемся к шагу 3.
В нашем случае задача решена.
План работ: 1B, 2D, 3A, 4C, 5E
Общие трудозатраты равны 12 дней. Делаем проверку, подставляем в первую матрицу и сравниваем, данные равны. 12=12.
Задача №2
Приближенные методы решения транспортной задачи.
Вариант №1
1. Метод северо-западного угла
| j | |||||
| i |  bj
| ||||
| ai | |||||
Рассматриваем клетку 11, осуществляем через нее перевозку, выбирая минимум из того что есть и того, что надо. Если вывезем весь товар из пункта отправки, то закрывается строка и переходим на клетку ниже. Если полностью удовлетворена потребность в пункте назначения, то закрывается столбец и переходим на клетку вправо.
С1=18×15+23×3+5×10+16×12+3×3+20×17+15×10+17×5=270+69+50+192+9+340+150+85=1165 у.е.
2. Минимум по строке.
| j | |||||
| i | bj
| ||||
| ai | |||||
В строке ищется минимальная стоимость и через эту клетку осуществляется перевозка, если строка открыта, то ищем следующую клетку с минимальной стоимостью. После того, как строка закрыта, переходим в следующей строке.
С2 = 15×13+6×5+5×10+3×15+9×2+7×15+21×13+15×2=195+30+50+45+18+105+
+273+30=746 у.е.
3. Минимум по столбцу.
| j | |||||
| i | bj
| ||||
| ai | |||||
Принцип решения такой же, как и в минимуме по строке, только теперь те же действия со столбцами.
С3 = 9×15+5×10+6×15+15×15+3×15+6×3+4×2=571 у.е.
4. Метод минимального элемента.
| j | |||||
| i | bj
| ||||
| ai | |||||
В матрице выбирается минимальный элемент, через который осуществляется перевозка, далее закрываются строки или столбцы, если это возможно. Ищется минимальный элемент среди открытых клеток и т.д.
С4 = 18×3+15×15+5×10+3×15+9×12+4×5+6×15=54+225+50+45+108+20+90=
=592 у.е.
Ответ: минимальная стоимость перевозки получается методом минимума по столбцу = 571 у.е.
Список литературы:
1. Аникин Б.Е. Логистика / Учебное пособие. М.: ИНФРА. 2000.
2. Гаджинский А.М. Логистика: Учебник для высших и средних спец. учебных заведений.– 6-е издание; переработанное и дополненное. М: Издательско-торговая корпорация «Дашков и Ко». -2003.–408 с.
3. Леншин И.А. Основы логистики: Уч. Пособие. М.: Машиностроение, 2002.
4. Семененко А.И, Сергеев В.И. Логистика. Основы теории: Учебник для вузов. — СПб.: Издательство «Союз», 2003. — 544 с.
5. Сайт https://learnlogistic.ru/
6. Лекции Карасев А.П.