Дифференциальное уравнение вида
где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка.
11. Дифференциальные уравнения II порядка вида y"=f(x) (способ решения).
называется дифференциальным уравнением второго порядка.
12. Линейные однородные дифференциальные уравнения II порядка с постоянными коэффициентами (общий вид, способ решения при различных случаях дискриминанта характеристического уравнения).
1)Запишем сначала соответствующее характеристическое уравнение:
2) Корни данного уравнения равны k 1 = 1, k 2 = 5. Поскольку корни действительны и различны, общее решение будет иметь вид:
где C 1 и C 2 − произвольные постоянные.
13. Определение числового ряда. Примеры числовых рядов.
Числовой ряд – это сумма членов числовой последовательности вида.
Пример: 
14. Определение сходящегося ряда. Сумма ряда.
сумма ряда - это (конечный) предел последовательности его частичных сумм.
Ряд 
называется сходящимся, если последовательность его частичных сумм 
сходится.
15. Необходимое условие сходимости ряда.
Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов.
16. Признаки сходимости рядов с неотрицательными членами: признак сравнения.
Признак сравнения — утверждение об одновременности расходимости или сходимости двух рядов, основанный на сравнении членов этих рядов.
Пусть даны два знакоположительных ряда:
Тогда, если, начиная с некоторого места 
выполняется неравенство: 
то из сходимости ряда следует сходимость 
.
17. Признаки сходимости рядов с неотрицательными членами: признак Даламбера.
Если для числового ряда
существует такое число 
, 
, что начиная с некоторого номера выполняется неравенство
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
то ряд расходится.
18. Признаки сходимости рядов с неотрицательными членами: радикальный признак Коши.
Если для числового ряда
с неотрицательными членами существует такое число 
что, начиная с некоторого номера, выполняется неравенство
то данный ряд сходится.
19. Знакочередующиеся ряды. Признак Лейбница для сходимости знакочередующегося ряда.
Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами.
1) Ряд является знакочередующимся.
2) Члены ряда убывают по модулю: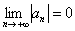 
Причём, убывают монотонно. Если выполнены оба условия, то ряд сходится.
20. Знакопеременные ряды. Достаточное условие сходимости знакопеременного ряда.
Функциональный ряд 1 называется сходимым в точке Хо, если числовой ряд 2, полученный из ряда 1 подстановкой Х=Хо, является сходимым рядом. При этом Хо называется точкой сходимости ряда.
21. Абсолютная и условная сходимость.
Ряд 
называется абсолютно сходящимся, если ряд 
также сходится.
Ряд называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.
22. Степенные ряды Теорема Абеля. Область сходимости и радиус сходимости степенного ряда.
Степенным рядом называется функциональный ряд вида
где a0, a1, a2, …,an,…, а также x0 – постоянные числа.
Если степенной ряд (1.2) сходится при некотором 
, где 
-число, не равное нулю, то он сходится абсолютно при всех значениях x таких, что 
Наоборот, если ряд (12) расходится при , то он расходится при всех значениях x таких, что 
23.Ряд Тейлора. Разложение элементарных функций в ряд Тейлора.
Пусть функция 
бесконечно дифференцируема в некоторой окрестности точки 
. Формальный ряд
называется рядом Тейлора функции 
в точке .
разложение в ряд функции f (x) = ex. Поскольку f (n)(x) = ex, то для любого фиксированного a > 0, для всех x 
(- a, a) и всех n = 1, 2,... выполняется неравенство
0 < f (n)(x) < ea.
24. Тригонометрические ряды. Ряды Фурье
Тригонометрическим рядом Фурье функции 
называют функциональный ряд вида
25. Разложение функций в ряды Фурье
Рассмотрим кусочно-непрерывную f (x), заданную в интервале [ − L, L ]. Используя подстановку 
, преобразуем ее в функцию
определенную и интегрируемую в интервале [ −π, π ]. Разложение в ряд Фурье для функции F (y) имеет вид
Коэффициенты Фурье для данной функции определяются формулами
