Последовательность выполнения задания. Замкнутый теодолитный ход

Замкнутый теодолитный ход

1. Определяют сумму измеренных углов замкнутого теодолитного хода (см. рис. 8) ∑βп и сравнивают ее с теоретиче­ской суммой

∑βт= 180° (n — 2), где n —число углов замкнутогохода. В нашем задании п=5,

∑βТ= 180° (5-2)-540°;

∑βп= 82°58,5/ + 154° 47' + 67°45'+ 79° 48' + 154°42,5' = 540°01'.

Угловая невязка определяется по формуле

fβ= ∑βп - ∑βт

fβ = ∑βп - 180° (n - 2),

fβ = 540°01' - 540° = +1'

Угловая невязка не должна быть более допустимой, определяемой по формуле

fβдоп≤ 1,5t ,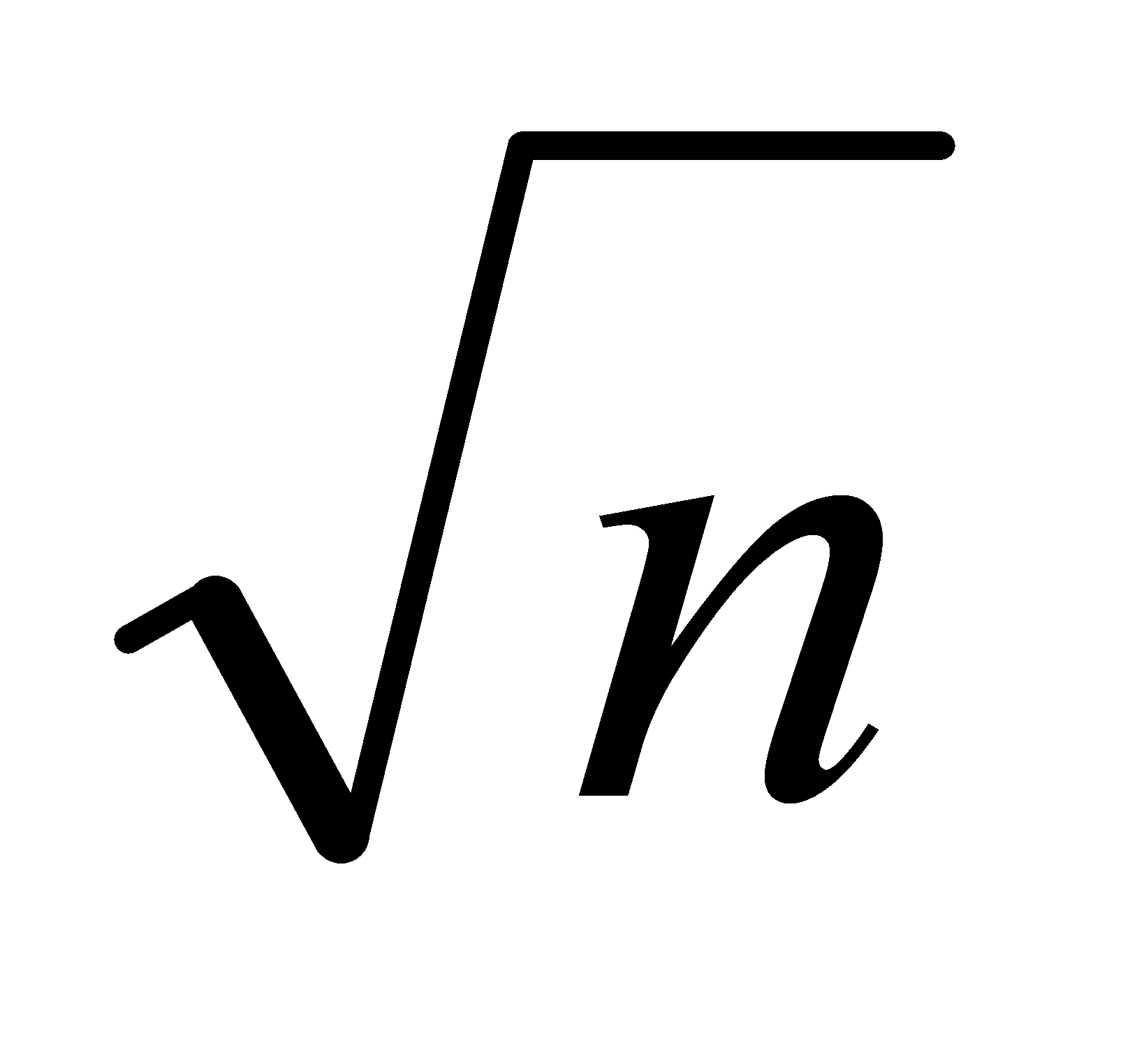

где t —точность верньера или точность отсчета по шкале микроскопа теодолита

п — число углов теодолитного хода.

Предельно допустимая невязка fβдоп≤ 1,5.30″ .

В задании невязка допустима 1'<1,5'.

Исправленные углы

 

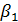=85⁰58,5^/-0,5=82⁰ 58,0^/

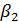=154⁰ 47^/

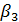=67⁰ 45^/

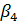=79⁰ 48^/

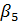=154⁰ 42,5^/-0,5^/=154⁰ 42,0^/

 

 

Сумма исправленных углов хода должна быть равна теоретической сумме:

∑βиспр= ∑βТ.

 

2. По заданному дирекционному углу, который указан в исходных данных (см. табл.14), и увязанным внутренним углам полигона вычисляют дирекционные углы всех остальных сторон хода по формуле:

ап = ап-1 + 180- β испр, (13)

где ап- дирекционный угол последующей линии,

ап-1 - дирекционный угол предыдущей линии,

β испр- исправленный угол, вправо по ходу лежащий.

а_n= а_n-1 + β исп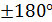

 

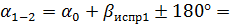61^°17^/ +82^°58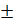^/ 180°=324^°15^/

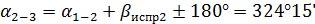+154⁰ 47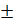^/ 180°=299^°02^/

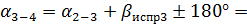299°20̍+67^°45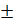^/ 180°=186^°47^/

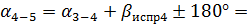186^°47^/ +79^°48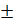^/ 180^° =86^°35^/

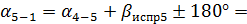86^°35^/ +154^°42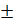^/ 180°=61^°17

 

^/

 

3. По найденным дирекционным углам вычисляют румбы сто­рон замкнутого теодолитного хода

α_1-2=324⁰15^/ r_1-2 =360-α_1-2 r_1-2 = 360°-324°15ʹ=СЗ:36°13ʹ

α_2-3=299⁰02^/ r_2-3 = 360°-α_2-3 r_2-3= 360⁰ -299⁰02ʹ =СЗ: 119⁰2^/

 

α_3-4=186⁰47^/ r_3-4= α_3-4-180° r_3-4 = 186°47ʹ- 180⁰ = ЮЗ: 6⁰47^/

 

α_4-5=86⁰35^/ r_4-5 = α_4-5 r_4-5=СВ: 86⁰35

α_5-1=61⁰17^/ r_5-1= α_5-1. r_5-1=СВ: 61⁰17^/

4. По румбам и горизонтальным приложениям сторон вычисляют приращения координат по формулам:

∆x =d cos r, ∆y =d sin r, или

∆x =d cos α, ∆y =d sin α.

где ∆x и ∆y - приращения координат.

При вычислении приращений координат можно пользоваться таблицами для вычисления прямоугольных координат, таблицами натуральных значений тригонометрических функций.

Знаки приращений координат зависят от направления линий

 

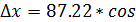324⁰15^/ = 70,78

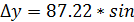324⁰15^/ =-50,96

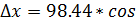299⁰20^/ = 47,77

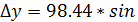299⁰20^/ = -86,06

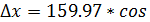186⁰47^/ = -158,85

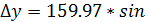186⁰47^/ = -18,89

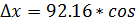86⁰35^/ = 5,49

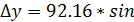86⁰35^/ =92,00

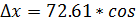61⁰17^/ =34,89

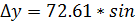61⁰17^/ = 63,68

 

5. Вычислив приращения координат, определяют их алгебраи­ческую сумму:

∑∆х = 0,08

∑∆y = -0,23

В замкнутом ходе сумма приращений координат теоретически должна быть равна нулю:

∑∆х = 0, ∑∆y = 0.

Практически алгебраическая сумма вычисленных прираще­ний несколько отличается от теоретической на величину невя­зок, т. е. абсолютная невязка определяется по формуле:

 

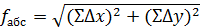
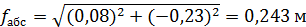
Относительная невязка определяется по формуле:

 

 

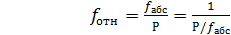
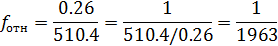
Относительная невязка не должна превышать периметра хода

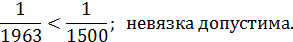
Если невязка допустима, необходимо ее распределить в виде поправок. Поправки распределяют пропорционально длинам сторон полигона.

Поправка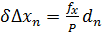

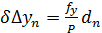
где Р – периметр хода в сотнях метров,

d – длина сторон хода в сотнях метров.

Поправки по оси Х

 

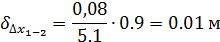
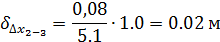
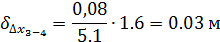
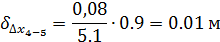
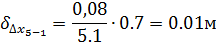
Поправки по оси Y

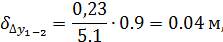
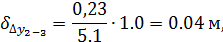
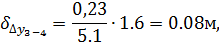
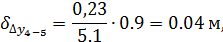
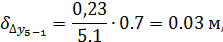
Сумма поправок на каждую из осей должна быть равна невязкам ΣΔx и ΣΔy.

Исправленные приращения определяют по формулам:

= - 0,05+ (- 0,05) = 0

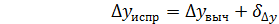=- 0,26+ (- 0,26) = 0

Поправки прибавляют к вычисленным приращениям со знаком, обратным знаку невязки.

Сумма исправленных приращений должна быть равна нулю

 

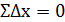
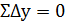
Определяют исправленные приращения:

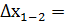70,78 - 0,01 = 70,78

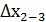=47,77- 0,02 = 47,75

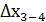= -158,85- 0,03 = -158,88

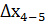=5,49 - 0,01 = 5,48

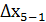= 34,89-0,01 = 34,88

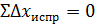
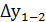= -50,96+ 0,04 = -50,92

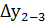= - 86,06+ 0,04 = - 86,02

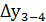= -18,89+ 0,08 = -18,81

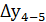= 92,00+ 0,04 = 92,04

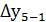= 63,68 + 0,03 = 63,71

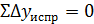
6. Координаты вершин полигона, определяются по формулам:

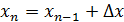(20)

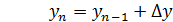(21)

где хn и yn – координаты последующей вершины,

х_n-1 и y_n-1 – координаты предыдущей вершины.

Контролем вычислений служит определение координат вершины 1 по координатам вершины 5 и приращений.

Определение координат

х₁= +18,00м, y₁= +10,00м

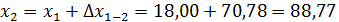
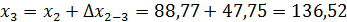
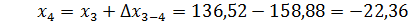
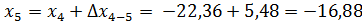
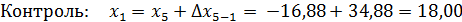
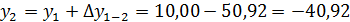
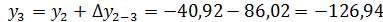
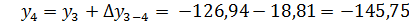
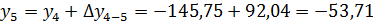
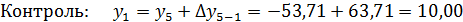
Составление плана полигона по координатам

№ точек	Измер.углы β	Исправл.углы β	Дирекц.углы α	Румбы r	Длина(м) d	Приращения координат	Координаты вершин
Вычисленные	Исправленные
ΔΧ	ΔΥ	ΔΧ	ΔΥ	Χ	Υ
1	2	3	4	5	6	7	8	9	10	11	12
1	82˚58,5'	82˚58'	324015/	СЗ:36°13	82,22	70,78	50,96	70,77	-50,92	88,77	-40,92
2	154˚47'	154˚47'	299020/	СЗ:11902/	98,44	47,77	-86,06	47,75	-86,02	136,52	-126,94
3	67˚45'	67˚45'	186047/	ЮЗ: 6047 /	159,97	-158,85	-18,89	-158,88	-18,81	-22,36	-145,75
4	79˚48'	79˚48'	86035/	СВ: 86035/	92,16	-5,49	92,00	5,48	92,04	-16,88	-53,71
5	154˚42,5'	154˚42'	61017/	СВ: 61017/	72,61	34,89	63,68	34,88	63,71	18,00	10,00
					540˚00'	Σ Δx=0,23,	Σ Δy=-0,13	Σ Δx=0.00	Σ Δy=0.00
f абс=√0,082+(-0,23)2=0,243 f отн= 0.26/432.11<1/2000