Расчётно-графическое задание № II
Колебательное движение маятника
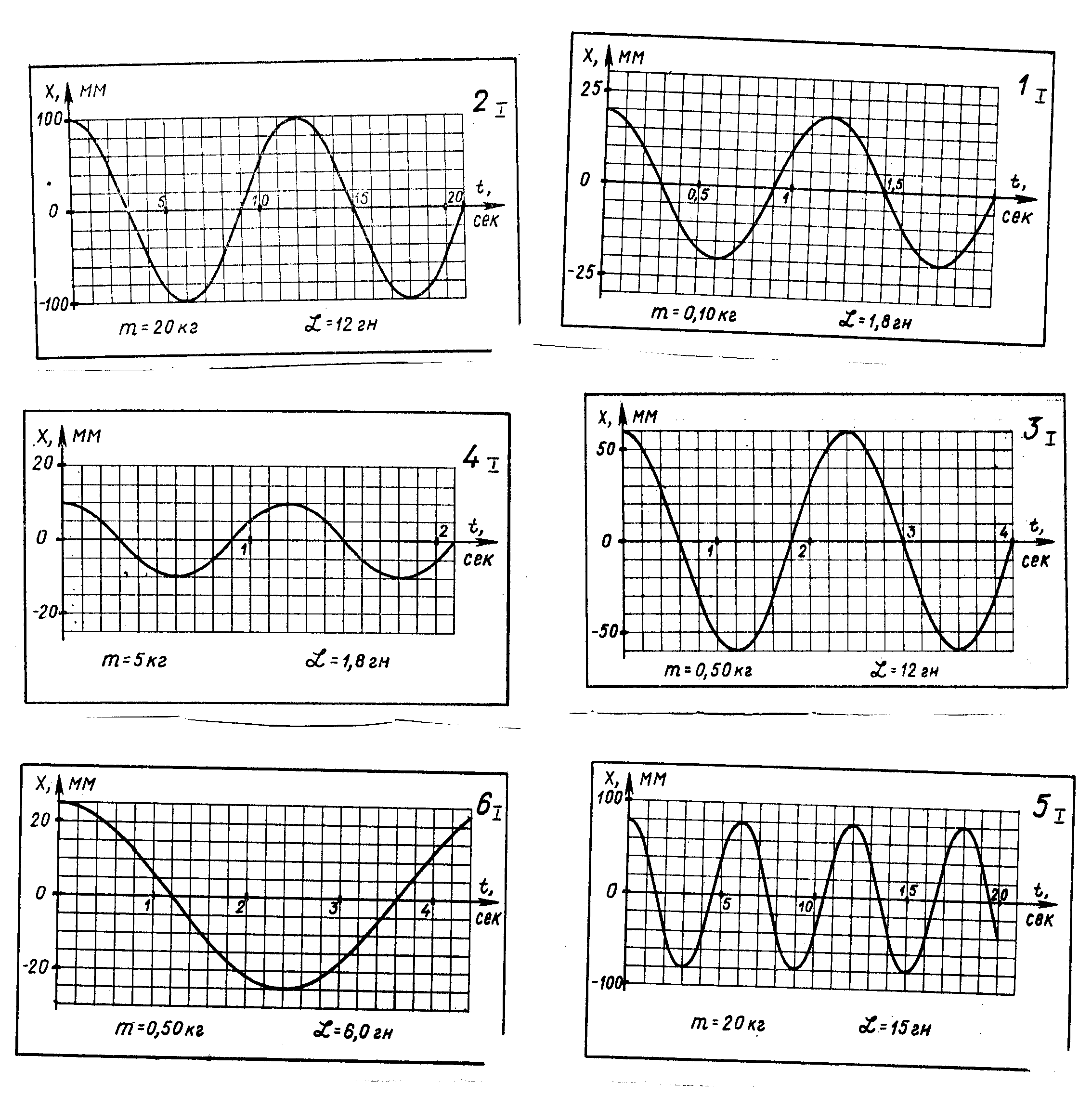
Вариант 1
Инструкция студентам по выполнению РГЗ
1. Прежде, чем приступить к выполнению РГЗ, изучите теоретический материал по данной теме. Его краткое изложение дано в описании.
2. РГЗ оформлено по плану:
- описание рисунка на карточке,
- вопросы к рисунку на карточке,
- таблица ответов,
- образец выполнения задания.
3. Внимательно изучите описание рисунка на карточке и вопросы, на которые необходимо ответить.
4. Оформление работы в тетради:
- Расчётно-графическое задание № ______
- Тема: ______________________________
- Вариант _________
- КАРТОЧКУ перерисовывать в тетрадь НЕ НУЖНО!!!
- нарисовать таблицу, в которую будете заносить ответы (Таблица 2),
- вычисляете задания по образцу,
- необходимые исходные данные берёте из рисунка 1, сравнивая его с рисунком 2 образца, некоторые данные находятся в пункте «вопросы »,
- если в задании указано «построить график», то его построение необходимо делать, применяя карандаш и линейку,
- при правильном решении обучающийся находит в таблице 1 в соответствующем этому вопросу столбце численный ответ на какой то строке и отмечает у себя в таблице 2 на этом же месте,
- если найденного числового ответа в таблице нет, то учащийся должен проверить решение и найти свою ошибку.
5. Вычисления при заполнении таблиц ответами делались в соответствии с правилами приближённых вычислений: в промежуточных ответах сохранялись три значащие цифры, а в окончательном результате – две. Округление чисел с добавлением единицы в последнюю цифру результата производилось тогда, когда последующая цифра была равна 5 и более.
Расчётно-графическое задание № 1
Колебательное движение маятника
Теоретический материал
Колебания – движения, повторяющиеся точно или приблизительно точно за равные промежутки времени.
Математический маятник – материальное тело, подвешенное на нерастяжимой нити, размерами которого пренебрегают по сравнению с длиной нити.
Гармонические колебания – колебания, совершаемые по закону синуса или косинуса:
Характеристики колебательного движения:
Амплитуда (Х max, м) – максимальное отклонение тела от положения равновесия,
Период (Т, с) – время, в течение которого тело совершает одно полное колебание,
Частота (
)– число колебаний за 1с.
Циклическая или собственная частота (
) – число колебаний за 2π с.
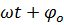– фаза колебаний, 
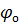- начальная фаза колебаний.
Формулы:
период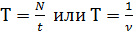 
, где N – число колебаний, t – время колебаний;
период математического маятника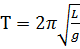 
, где L – длина маятника;
период маятника на пружине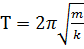 
, где m – масса груза, k – жёсткость пружины или коэффициент упругости;
частота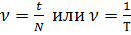 
;
собственная или циклическая частота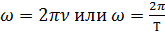 
Описание рисунка 1
На рисунке изображён график зависимости смещения от времени при колебательном движении математического маятника.
| Вопросы: 1. Какова амплитуда колебательного движения? 2. Каков период колебания? 3. Вычислите частоту колебания маятника. 4. Какой длины математический маятник колеблется с этой же частотой? (для простоты вычисления полагать π2 = 10, g = 10 м/с2). |
5. Определите смещение маятника при фазе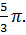 
Перечертите график в тетрадь и укажите на нём это смещение.
6. Вычислите циклическую частоту.
7. Какой наибольший модуль скорости имеет маятник при колебаниях?
8. Вычислите кинетическую энергию в этот момент.
9. Вычислите скорость при фазе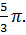
10. Вычислите ускорение при фазе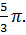
11. Вычислите равнодействующую силу при фазе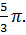
12. Вычислите кинетическую и потенциальную энергии при фазе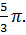
13. Какой жёсткости должна быть пружина для маятника, чтобы та же масса груза колебалась в вертикальной плоскости с частотой в 10 раз больше? (Массой пружины пренебречь).
14. Какое удлинение получит эта пружина, когда к ней подвесят данный груз?
15. Конденсатор какой электроёмкости надо поставить в колебательный контур с той индуктивностью, которая указана на карточке, чтобы в нём происходили электромагнитные колебания с частотой в 100 раз меньшей, чем у математического маятника, описанного в карточке?
16. Ответы занесите в таблицу 2, используя таблицу 1 «Варианты ответов».
