1 Цель работы:
1.1 Исследование рекурсивного звена 2-го порядка во временной области, z-области и частотной области
2 Литература:
2.1 Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Издание 3-е, исправленное. — Москва: Техносфера 2012 г.— 1048 с.
2.2 Умняшкин С. В. Теоретические основы цифровой обработки и представления сигналов: Учебное пособие. — Москва: Техносфера 2012 г.— 368 с. — Электронное издание.
3 Основное оборудование:
3.1 Персональный компьютер.
3.2 Калькулятор
4 Подготовка к работе:
4.1 Повторить материал лекций по теме "Описание дискретных сигналов в спектральной области"
4.2 Изучить методику расчета импульсной характеристики
4.3 Повторить методику расчета АЧХ и ФЧХ фильтров
5 Задание:
5.1 являются коэффициенты передаточной функции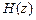 
, приведенные в табл. 1. Вариант выбирается по двум последним цифрам номера зачетной книжки (всего 100 вариантов).
Все расчеты выполняются с точностью до 4-го знака после запятой.
Задание на контрольную работу для всех вариантов включает следующие пункты:
1. Записать передаточную функцию (ПФ).
2. Записать разностное уравнение (РУ).
3. Изобразить структурную схему.
4. Записать формулу импульсной характеристики (ИХ) с учетом нулевых начальных условий.
5. Рассчитать 5 отсчетов ИХ по полученной формуле.
6. Рассчитать 5 отсчетов ИХ с помощью РУ.
7. Сравнить результаты вычислений пп. 5, 6.
8. Построить график ИХ (5 отсчетов).
9. Изобразить карту нулей и полюсов.
10. Записать формулы для расчета АЧХ и ФЧХ в произвольной точке.
11. Сделать вывод о качественном характере АЧХ и ФЧХ по карте нулей и полюсов.
12. Выполнить экспресс-анализ АЧХ и ФЧХ.
13. Построить графики АЧХ и ФЧХ по результатам пп. 11–12.
Таблица 1 Варианты и исходные данные для КР
| № | Коэффициенты передаточной функции | ||||
| 
| 
| 
| 
| |
| – 0,7857 | 0,6904 | 0,64 | |||
| – 1,07 | 0,77 | 0,71 | 0,56 | ||
| 0,87 | 0,73 | ||||
| 0,6429 | 0,999 | – 1,01 | 0,8 | ||
| – 2 | – 0,88 | 0,68 | |||
| 1,01 | 0,8 | ||||
| – 1 | 0,57 | 0,62 | |||
| –1,05 | 0,67 | ||||
| 1,07 | 0,77 | – 0,71 | 0,56 | ||
| – 0,6429 | 0,999 | 0,71 | 0,56 | ||
| – 1,143 | 0,7631 | 0,7 | |||
| – 0,4 | 0,63 | 1,14 | 0,77 | ||
| – 0,87 | 0,73 | ||||
| 1,571 | 1,008 | – 0,97 | 0,72 | ||
| – 2 | 0,88 | 0,68 | |||
| 0,97 | 0,72 | ||||
| – 1 | – 0,57 | 0,62 | |||
| 1,05 | 0,67 | ||||
| 0,4 | 0,63 | – 1,14 | 0,77 | ||
| – 1,571 | 1,008 | 1,14 | 0,77 | ||
| – 0,9643 | 0,6231 | 0,75 | |||
| – 0,25 | 0,58 | 0,93 | 0,75 | ||
| 0,75 | 0,78 | ||||
| 0,75 | 1,003 | – 0,46 | 0,76 | ||
| – 2 | – 0,77 | 0,84 | |||
| 0,46 | 0,76 | ||||
| – 1 | 1,07 | 0,71 | |||
| – 1,16 | 0,71 | ||||
| 0,25 | 0,58 | – 0,93 | 0,75 | ||
| – 0,75 | 1,003 | 0,93 | 0,75 | ||
| – 0,6071 | 0,6818 | 0,78 | |||
| – 1,25 | 0,76 | 0,68 | 0,57 | ||
| – 0,75 | 0,78 | ||||
| 1,5 | 0,999 | – 0,96 | 0,67 | ||
| – 2 | 0,77 | 0,84 | |||
| 0,96 | 0,67 | ||||
| – 1 | – 1,07 | 0,71 | |||
| 1,16 | 0,71 | ||||
| 1,25 | 0,76 | – 0,68 | 0,57 | ||
| – 1,5 | 0,999 | 0,68 | 0,57 | ||
| – 1,429 | 0,7789 | 0,81 | |||
| – 0,71 | 0,69 | 1,28 | 0,52 | ||
| 0,64 | 0,69 | ||||
| 0,4467 | 0,9998 | – 1,07 | 0,61 | ||
| – 2 | – 0,65 | 0,82 | |||
| 1,07 | 0,61 | ||||
| – 1 | 0,65 | 0,82 | |||
| – 0,64 | 0,69 | ||||
| 0,71 | 0,69 | – 1,28 | 0,52 | ||
| – 0,4467 | 0,9998 | 1,28 | 0,52 | ||
| 0,7857 | 0,6904 | 0,64 | |||
| – 0,43 | 0,78 | 1,07 | 0,61 | ||
| – 0,64 | 0,69 | ||||
| 1,198 | 1,002 | – 1,28 | 0,52 | ||
| – 2 | 0,65 | 0,82 | |||
| 1,28 | 0,52 | ||||
| – 1 | – 0,65 | 0,82 | |||
| 0,64 | 0,69 | ||||
| 0,43 | 0,78 | – 1,07 | 0,61 | ||
| № |
|
|
|
|
|
| – 1,198 | 1,002 | 1,07 | 0,61 | ||
| 1,143 | 0,7631 | 0,75 | |||
| – 0,43 | 0,78 | 0,96 | 0,67 | ||
| 1,16 | 0,71 | ||||
| 0,3249 | 0,9962 | – 0,68 | 0,57 | ||
| – 2 | – 1,07 | 0,71 | |||
| 0,68 | 0,57 | ||||
| – 1 | 0,77 | 0,84 | |||
| – 0,75 | 0,78 | ||||
| 0,43 | 0,78 | – 0,96 | 0,67 | ||
| – 0,3249 | 0,9962 | 0,96 | 0,67 | ||
| 0,9643 | 0,6231 | 0,81 | |||
| – 0,32 | 0,79 | 0,46 | 0,76 | ||
| – 1,16 | 0,71 | ||||
| 0,3249 | 0,9962 | – 0,93 | 0,75 | ||
| – 2 | 1,07 | 0,71 | |||
| 0,93 | 0,75 | ||||
| – 1 | – 0,77 | 0,84 | |||
| 0,75 | 0,78 | ||||
| 0,32 | 0,79 | – 0,46 | 0,76 | ||
| – 0,3249 | 0,9962 | 0,46 | 0,76 | ||
| 0,6071 | 0,6818 | 0,72 | |||
| – 0,44 | 0,65 | 0,97 | 0,72 | ||
| 1,05 | 0,67 | ||||
| 0,4873 | 1,009 | – 1,14 | 0,77 | ||
| – 2 | – 0,57 | 0,62 | |||
| 1,14 | 0,77 | ||||
| – 1 | 0,88 | 0,68 | |||
| – 0,87 | 0,73 | ||||
| 0,44 | 0,65 | – 0,97 | 0,72 | ||
| – 0,4873 | 1,009 | 0,97 | 0,72 | ||
| 1,429 | 0,7789 | 0,81 | |||
| – 0,54 | 0,61 | 1,01 | 0,8 | ||
| –1,05 | 0,67 | ||||
| 0,9746 | 0,9998 | – 0,71 | 0,56 | ||
| – 2 | 0,57 | 0,62 | |||
| 0,71 | 0,56 | ||||
| – 1 | – 0,88 | 0,68 | |||
| 0,87 | 0,73 | ||||
| 0,54 | 0,61 | – 1,01 | 0,8 | ||
| – 0,9746 | 0,9998 | 1,01 | 0,8 | ||
| 0А | – 0,7 | 0,49 | |||
| 0В | – 1 | – 0,7 | 0,49 | ||
| 0С | 0,7 | 0,49 | – 0,7 | 0,49 |
Примечание.
1. Для всех вариантов полюсы – комплексно-сопряженные.
2. При выполнении контрольной работы должны быть приведены все необходимые расчетные формулы.
3. Значение угла j следует задавать относительно p, например, если j* = 1,7654, то необходимо записать 
.
6 Содержание отчета:
6.1 Наименование работы
6.2 Цель работы.
6.3 Выполнение заданий согласно пункту 5
6.4 Ответы на контрольные вопросы
7 Контрольные вопросы:
7.1 Какова связь передаточной функции и разностного уравнения?
7.2 Чем является импульсная характеристика?
7.3 Что такое "дельта-функция"?
7.4 Чем похожи, а чем различны дельта функция и белый шум?
ПРИЛОЖЕНИЕ
Пример 1. Вариант 0А (табл. 1, внизу).
Исходные данные – коэффициенты ПФ 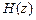2-го порядка:
Решение
1. Запишем ПФ на основе ее общего вида
. (1)
Исследуемое звено является базовым, так как числитель передаточной функции 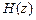равен 1.
2. Используя методику нахождения импульсной характеристики, на основе РУ общего вида (1.50) получаем
. (2)
3. На основе структурной схемы рекурсивного звена 2-го порядка общего вида имеем схему рис. 1.
Рис. 1. Структурная схема базового звена 2-го порядка
4. На основе общей формулы импульсной характеристики базового звена с учетом нулевых начальных условий запишем
, 
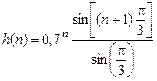, (3)
где значения 
и 
рассчитаны и равны:
;
.
5. Результаты расчета 5 точек ИХ по формуле (3) с точностью до 4-го знака после запятой приведены в табл. 1.
Таблица 3.1 Вычисление ИХ по формулам
| n | h(n), рассчитанная по (3.3) |
| |
| |
| |
| |
|
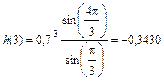
6. Расчет ИХ по РУ выполняется методом прямой подстановки при нулевых начальных условиях.
Выполнив в РУ (2) подстановку, запишем уравнение
, (4)
результаты решения которого при нулевых начальных условиях с точностью до 4-го знака после запятой приведены в табл. 2.
Таблица 2 Вычисление ИХ по РУ (4)
| n | h(n), рассчитанная по (3.4) |
| |
| |
| |
| |
|
7. Результаты вычислений ИХ двумя способами в пп. 5, 6 совпадают.
8. График ИХ (5 отсчетов) представлен на рис. 2.
Рис. 2. Импульсная характеристика
9. Для построения карты нулей и полюсов необходимо вычислить нули и полюсы ПФ по соответствующей методике.
Комплексно-сопряженные полюсы в показательной форме
с учетом рассчитанных в п. 4 значений и равны
.
Для определения комплексно-сопряженных нулей умножим числитель и знаменатель ПФ на 
, получим
и найдем корни числителя – нули ПФ
.
В данном примере имеем два одинаковых вещественных нуля, такие нули называют кратными.
Рис. 3. Карта нулей и полюсов
Карта нулей и полюсов изображена на рис. 3 а; та же карта с необходимыми комментариями приведена на рис. 3.3 б.
10. Для расчета значений АЧХ и ФЧХ звена 2-го порядка в произвольной точке необходимо использовать общие формулы:
;
подставляя в них заданные значения коэффициентов.
11. Качественный анализ АЧХ и ФЧХ по карте нулей и полюсов выполняется на основе соответствующей методики, которую предварительно необходимо внимательно изучить.
В данном случае карта нулей и полюсов содержит два комплексно-сопряженных полюса и два кратных нуля ПФ, равных нулю, поэтому относительно АЧХ можно сделать следующие выводы.
В основной полосе частот 
АЧХ звена 2-го порядка является гладкой функцией, при этом:
- внутри основной полосы частот АЧХ имеет один максимум, расположенный на частоте полюса 
;
- внутри основной полосы частот АЧХ не имеет минимума;
- на границах основной полосы частот 
и 
АЧХ имеет минимумы.
Относительно ФЧХ можно сказать, что внутри основной полосы частот и на ее границах ФЧХ представляет собой непрерывную функцию, не имеющую скачков.
12. Экспресс-анализ АЧХ и ФЧ:
В данном примере следует вычислить значения АЧХ и ФЧХ в четырех точках:
а) в точке при 
;
;
б) в точке 
при 
;
;
в) в точке 
при 
;
г) в точке максимума АЧХ 
, который находится приблизительно на частоте полюса [1]
; 
.
Значения АЧХ и ФЧХ в этой точке, равны
; 
.
13. Графики нормированных АЧХ и ФЧХ, построенные на основе качественного анализа и экспресс-анализа, представлены на рис. 4.
Рис. 4. Графики нормированных АЧХ и ФЧХ
Примечание. В практической работе студенты могут строить нормированную либо ненормированную АЧХ.
Пример 2. Вариант 0В (табл. 1, внизу).
Исходные данные – коэффициенты ПФ 
2-го порядка:
Решение
1. Запишем ПФ на основе ее общего вида
. (1а)
Исследуемое звено не является базовым.
Знаменатели ПФ небазового (1а) и базового (1) звеньев совпадают, поэтому основное внимание в данном примере будет уделено анализу «влияния числителя» и студенту предварительно следует изучить пример 1.
2. На основе РУ общего вида получим
. (2а)
3. На основе структурной схемы рекурсивного звена 2-го порядка общего вида имеем схему (рис. 5).
Рис. 5. Структурная схема базового звена 2-го порядка
4. На основе общей формулы импульсной характеристики небазового звена с учетом нулевых начальных условий запишем
(3а)
где значения 
и 
, рассчитаны в п. 4 примера 1.
5. Результаты расчета 5 точек ИХ по формуле (3а) с точностью до 4-го знака после запятой приведены в табл. 2а.
Таблица 2а - Вычисление ИХ по формуле (3а)
| n | h(n), рассчитанная по (3.3а) |
| |
| |
| |
| |
|
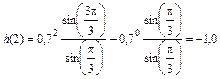
6. Расчет ИХ по РУ выполняется методом прямой подстановки при нулевых начальных условиях.
Выполнив в РУ (2а) подстановку, запишем уравнение
, (3.4а)
результаты решения которого с точностью до 4-го знака после запятой приведены в табл. 3а.
Таблица 3а - Вычисление ИХ по РУ (4а)
| n | h(n), рассчитанная по (3.4а) |
| |
| |
| |
| |
|
7. Результаты вычислений ИХ двумя способами в пп. 5, 6 совпадают.
8. График ИХ (5 отсчетов) представлен на рис. 6.
Рис. 6. Импульсная характеристика
9. Для построения карты нулей и полюсов необходимо вычислить нули и полюсы ПФ
Комплексно-сопряженные полюсы, вычисленные в примере 1, п.4, равны
.
Для определения нулей умножим числитель и знаменатель ПФ на 
, получим
,
и найдем корни числителя
; 
; 
,
которые являются вещественными нулями.
Карта нулей и полюсов изображена на рис. 7а; та же карта с необходимыми комментариями приведена на рис. 7б.
Рис. 3.7. Карта нулей и полюсов
10. См. п. 10 в примере 1.
11. Качественный анализ АЧХ и ФЧХ по карте нулей и полюсов.
В данном случае карта нулей и полюсов содержит два комплексно-сопряженных полюса (таких же, как в примере 1) и два нуля, лежащих на единичной окружности на границах основной полосы частот, поэтому относительно АЧХ можно сделать следующие выводы.
В основной полосе частот 
АЧХ звена 2-го порядка (5а) является непрерывной функцией, при этом:
- внутри основной полосы частот АЧХ имеет один максимум, расположенный приблизительно на частоте полюса 
;
- внутри основной полосы частот АЧХ не имеет минимума;
- на границах основной полосы частот и 
АЧХ равна нулю; нули АЧХ не являются ее минимумами.
Относительно ФЧХ можно сказать, что она представляет собой непрерывную функцию, имеющую на границах основной полосы скачки.
12. Экспресс-анализ АЧХ и ФЧХ.
Рис. 8. Графики нормированной АЧХ и ФЧХ
В данном примере следует вычислить значения АЧХ и ФЧХ в двух точках:
а) в точке 
при
;
б) в точке максимума АЧХ 
, который находится приблизительно на частоте 
полюса
; 
.
Значения АЧХ и ФЧХ в этой точке равны:
; 
.
13. Графики нормированной АЧХ и ФЧХ, построенные на основе качественного анализа и экспресс-анализа, представлены на рис. 8.
Пример 3. Вариант 0С (табл. 1, внизу).
Исходные данные – коэффициенты ПФ 
2-го порядка:
Решение
1. Запишем ПФ на основе ее общего вида
. (1б)
Исследуемое звено не является базовым.
Знаменатели ПФ небазового (1а) и базового (1) звеньев совпадают, поэтому основное внимание в данном примере, так же как в примере 2, будет уделено анализу «влияния числителя» и студенту предварительно следует изучить пример 1.
2. Используя методику п. 1.4.3, на основе РУ общего вида получим
(2б)
3. На основе структурной схемы рекурсивного звена 2-го порядка общего вида имеем схему рис. 9.
Рис. 9. Структурная схема базового звена 2-го порядка
4. На основе общей формулы импульсной характеристики небазового звена с учетом нулевых начальных условий запишем
(3б)
где значения и рассчитаны в п. 4 примера 1.
5. Результаты расчета 5 точек ИХ по формуле (3б) с точностью до 4-го знака после запятой приведены в табл. 2б.
6. Расчет ИХ по РУ выполняется методом прямой подстановки при нулевых начальных условиях.
Выполнив в РУ (2б) подстановку, запишем уравнение
(4б)
результаты решения которого при нулевых начальных условиях приведены в табл. 3б.
7. Результаты вычислений ИХ двумя способами в пп. 5, 6 совпадают.
Таблица 2б - Вычисление ИХ по формуле 3б)
| n | h(n), рассчитанная по (3.3б) |
| |
| |
| |
| |
|
Таблица 2б - Вычисление ИХ по РУ (4б)
| n | h(n), рассчитанная по (3.4б) |
| |
| |
| |
| |
|
8. График ИХ (5 отсчетов) представлен на рис. 10.
Рис. 3.10. Импульсная характеристика
9. Для построения карты нулей и полюсов необходимо вычислить нули и полюсы ПФ
Комплексно-сопряженные полюсы вычислены в примере 1, п. 4:
.
Для определения нулей умножим числитель и знаменатель ПФ (1б) на 
получим
и найдем корни числителя
которые являются комплексно-сопряженными нулями
,
или в показательной форме
,
где
;
.
Карта нулей и полюсов изображена на рис. 3.11а; та же карта с необходимыми комментариями приведена на рис. 3.11б.
Рис. 11. Карта нулей и полюсов
10. См. п. 10 в примере 1.
11. Качественный анализ АЧХ и ФЧХ по карте нулей и полюсов.
В данном случае карта нулей и полюсов содержит два комплексно-сопряженных полюса (таких же, как в примерах 1 и 2) и два комплексно-сопряженных нуля, не лежащих на единичной окружности, поэтому относительно АЧХ можно сделать следующие выводы.
В основной полосе частот АЧХ звена 2-го порядка является гладкой функцией, при этом:
- внутри основной полосы частот АЧХ имеет один максимум, расположенный приблизительно на частоте полюса ;
- внутри основной полосы частот АЧХ имеет один минимум, расположенный приблизительно на частоте нуля 
;
- на границах основной полосы частот АЧХ имеет экстремумы: на частоте 
– минимум, а на частоте – максимум.
Относительно ФЧХ можно сказать, что она представляет собой непрерывную функцию, не имеющую ни на границах, ни внутри основной полосы частот скачков.
12. Экспресс-анализ АЧХ и ФЧХ.
В данном примере следует вычислить значения АЧХ и ФЧХ в пяти точках:
а) в точке при 
;
;
б) в точке при 
;
;
в) в точке 
при
;
г) в точке максимума АЧХ , который находится приблизительно на частоте полюса
; .
Значения АЧХ и ФЧХ в этой точке равны:
; 
;
д) в точке минимума АЧХ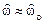 
, который находится приблизительно на частоте 
нуля
; 
.
Значения АЧХ и ФЧХ в этой точке равны:
; 
.
13. Графики нормированной АЧХ и ФЧХ, построенные на основе качественного анализа и экспресс-анализа, представлены на рис. 12.
Рис. 12. Графики нормированной АЧХ и ФЧХ
Рассмотренные выше примеры 1–3 являются типовыми, их внимательное изучение поможет студенту выполнить практическую работу для любого варианта табл. 1.