Режимы движения жидкостей. Турбулентное течение. Осредненная скорость.

Режимы движения жидкостей. Турбулентное течение. Осредненная скорость. Понятие о пограничном слое. Гидравлический радиус и эквивалентный диаметр.

Режимы движения жидкостей. Турбулентное течение. Осредненная скорость.

Первым указал на существование двух различных режимов течения жидкости в трубах крупнейший деятель техники Н.П.Петров* (1836-1920), когда в 1870-е годы разрабатывал гидродинамическую теорию смазки.

* Н.П. Петров -первый разработал технологию перевозки и хранения зерна и угля. Под его наблюдением строилась великая Транссибирская магистраль.

В первом режиме жидкость движется прямолинейно и параллельно оси трубы в виде вложенных один в другой цилиндрических слоев, движение которых напоминает удлинение раздвижной телескопической трубы. Во втором режиме в движущейся жидкости появляются вихри, разрывы, поперечные движения. Это наблюдение Петрова стало ключевой идеей в замечательных открытиях английского гидродинамика О. Рейнольдса.

.

Рис.1 Опыт Рейнольдса (1883 г).

При небольших расходах жидкости (а) струйка индикатора вытягивается в тонкую нить, т.е. частицы перемещаются по параллельным траекториям. При этом не происходит обмена частицами между слоями. Такое движение называется ламинарным (вязким, струйным, слоистым). Распределение скоростей при этом режиме подчиняется параболическому закону (рис.2)

Рис.2 Кривая распределения скорости по сечению потока

W_r=W_max(1-r²/R²)

W_max=2W_ср

Вблизи стенки скорость равна 0, по мере приближения к оси трубопровода увеличивается, достигая на самой оси max. С увеличением расхода жидкости (или скорости) сверх определенного предела окрашенная струйка приобретает поначалу волнообразное движение, затем начинает размываться и полностью окрашивает всю массу жидкости. Это объясняется тем, что на главное движение жидкости, происходящее в направлении оси трубопровода, налагается поперечное движение, вызванное поперечными пульсациями скорости. Это движение направлено перпендикулярно оси трубопровода. В результате частицы движутся по хаотическим траекториям.

 

Движение жидкости, когда вся масса её перемещается в одном направлении, а отдельные частицы (или группы частиц) движутся по хаотичным, неупорядоченным траекториям, называются турбулентным.

Теоретически описать профиль скорости в этом случае очень сложно, поэтому кривая W/Wmax выражает распределение не истинных, а осредненных во времени скоростей (рис.3). Использование этих скоростей позволяет приближённо рассматривать турбулентное движение как установившееся (турбулентное течение – квазистационарное)

 

 

W_x

Мгновенная пульсационная скорость

∆

Осредненная по времени

Истинная

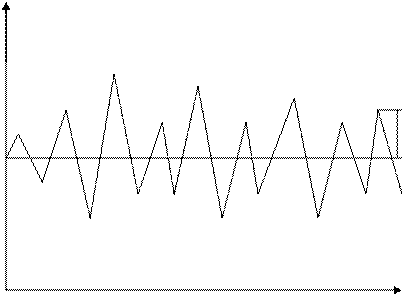
τ

 

=

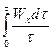
Рис.3. Изменение истинной скорости во времени

(Если W пульсаций близки или равны по своему значению, то такой турбулентный поток – изотропный)

 

При ламинарном и турбулентном течениях изменение скорости от Wmax в центре до 0 у стенки идёт по различным законам (рис.4).

Обнаружено при экспериментальном измерении профиля осреднённых по времени скоростей, что есть некоторый слой толщиной δ_л, где пульсации затухают, т.е. движение становится ламинарным (рис.4).

То есть, у стенки труб (или у границы раздела фаз) образуется область ламинарного подслоя (δ_л). В этом ламинарном подслое происходит максимальный grad W. Область перехода от турбулентного режима в основном объёме жидкости к ламинарному принято называть промежуточной областью. Обе области - гидродинамический пограничный слой. Ядро потока – основная часть. Пограничный слой составляет всего 1%, но роль его огромна для многих процессов.

r

турб

 

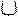
лам турб ядро

δ_п

w погран

Ламинарный (вязкий слой)

δ_л слой

 

 

Рис.4.

Важно отметить, что какими бы ни были высокими скорости течения, у границы раздела фаз всегда есть область вязкого течения.

Идея о пограничном слое, где следует учитывать силы трения, а вне пограничного слоя силами трения пренебречь вследствие их малости, принадлежит Прандтлю *.

Таким образом, в пограничном слое может быть как ламинарное, так и турбулентное течение. Толщина пограничного слоя – величина приблизительная, т.к. изменение скорости идёт асимптотически (поэтому вычисления зависят от точности, которую мы назначаем для равенства скоростей Wпогр ≈ Wвнешнего потока.

* Один из гидродинамических парадоксов, который очень долго беспокоил специалистов: почему в воде и в воздухе – жидкостях с довольно малой вязкостью, в которых сила трения гораздо меньше сил инерции и давления, при движении тел возникают сопротивления, огромные по сравнению с теоретически вычисленными.

В поисках ответа Прандтль в 1904 году показал, что движущееся тело как бы обволакивается тонким слоем жидкости – пограничным слоем. Благодаря вязкости внутренние частицы этого слоя как бы прилипают к стенке, и их скорость относительно тела равна нулю. На поверхности же пограничного слоя скорость частиц равна скорости обтекания. В тончайшем пограничном слое Fтрения сравнимы с Fинерции и давления, а вне его пренебрежимо малы.

 

 

Действие пульсационного движения на осредненное равнозначно увеличению вязкости осредненного движения. Эту кажущуюся вязкость принято называть турбулентной вязкостью. Турбулентная вязкость в отличие от молекулярной вязкости является функцией скорости потока.

W_TdW Тогда можно условно записать

W по аналогии с уравнением Ньютона

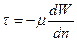; τ ~ удельный поток количества движения

- поток количества движения через единицу поверхности в единицу времени, т.е. поток количества движения от слоя с большей W к слою с меньшей скоростью пропорционален градиенту скорости. При ламинарном движении происходит перенос импульса силами молекулярного взаимодействия. При турбулентном за счет интенсивного перемешивания слоев тоже происходит обмен количеством движения, но в результате обмена пакетов молекул (иногда говорят вихрей, но это не точно), имеющих разную скорость.

если , т.е. турбулентный обмен импульсами много интенсивнее молекулярного обмена, при а внутри ламинарного подслоя

Число Re

Поскольку гидродинамический режим во многом определяет характер процессов, происходящих в потоке (тепло-, массообмен, химические реакции), то необходимо иметь критерий, позволяющий судить о режиме течения жидкости.

Такой критерий (или безразмерная величина) был предложен О. Рейнольдсом, который изучал движение жидкостей в круглой трубе. Он получил безразмерную величину, которую впоследствии (в 1919 г) стали называть его именем – числом Рейнольдса (Re). Это число управляет движением вязких жидкостей в трубах. Он предложил, что устойчивость ламинарного течения зависит от соотношения сил вязкости и сил инерции.

; l - определяющий геометрический размер

если Re < 2300 – течение всегда ламинарное (в прямой гладкой трубе)

- течение устойчивое турбулентное.

Затем выяснилось, что число Re, как и все критерии, имеет серьезный физический смысл.

Согласно закону трения Ньютона, сила трения Т пропорциональна площади трения , вязкости и градиенту скорости

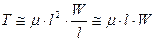
II закон механики: Сила инерции I пропорциональна массе и ускорению

отношение их

Если преобладают силы инерции I, т.е. численное значение Re велико, то течение турбулентно; если преобладают силы трения, Re мал – то течение вязкое (ламинарное).

Критическое значение Re (т.е. момент перехода ламинарного в турбулентное) устанавливается экспериментально и зависит от условий течения:

- в трубах (прямых, гладких, кривых);

- в стекающей пленке;

- течение сквозь зернистый слой;

- обтекание тел.

В качестве определяющего линейного размера l при движении жидкости через поперечное сечение каналов любой формы, отличной от круглой, принимают гидравлический радиус или эквивалентный диаметр.

Гидравлический радиус – отношение площади поперечного сечения потока в трубопроводе или канале к его смоченному периметру.

Для круглой трубы при сплошном ее заполнении жидкостью:

Диаметр, выраженный через гидравлический радиус, называют эквивалентным диаметром:

1. Для канала круглого сечения:

2. Для канала кольцевого поперечного сечения:

 

3. Для канала квадратного сечения:

4. Для канала прямоугольного сечения:

 

Немецкий инженер Г. Гаген (1797-1884), занимался инженерной деятельностью, спроектировал военно-морскую базу в Вильгельмсхафене. В 1839 г. Гаген опубликовал результаты своих обширных исследований по изучению влияния температуры на сопротивление жидкости, текущей в трубкахмалогодиаметра, в ходе которых он установил формулу для вычисления сопротивления.

Одновременно с ним во Франции аналогичные эксперименты провел врач Ж. Пуазейль (1799-1869), который изучал мощность сердца и движения крови в венах и капиллярных сосудах. Получил выводы о сопротивлении жидкости, аналогично гагеновой.

 

 

Гидродинамическое сопротивление.

Потери энергии на трение и местные сопротивления.

Течение в трубах.Число Рейнольдса.Ламинарное и турбулентное течения.

Понятие гидравлического радиуса и эквивалентного диаметра.

Эмпирические соотношения для расчета коэффициента трения.