Расчет режима электрической сети по нелинейным узловым уравнениям при задании нагрузок в мощностях с использованием итерационных методов.
Расчет режима электрической сети методом простой итерации (уравнения узловых напряжений в форме баланса токов и обращенная форма уравнений узловых напряжений)
Организуем итерационный процесс на базе матричного уравнения:
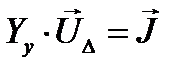
где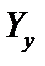 
- матрица узловых проводимостей без учета балансирующего узла,
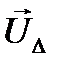- вектор-столбец падений напряжений в узлах сети, относительно балансирующего узла,
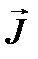- вектор-столбец задающих токов.
Оставим в левой части уравнения лишь вектор-столбец падений напряжений.
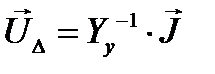
Распишем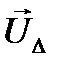 
как разность напряжений в узлах 
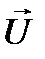и напряжения в балансирующем узле 
:
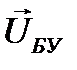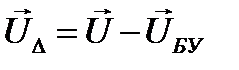
Приравняем правые части уравнений:
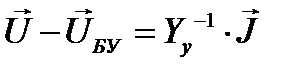
Выразим вектор-столбец напряжений в узлах:
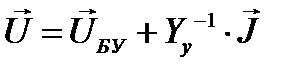
Выразим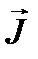 
через задающую мощность в узлах и напряжения в узлах схемы:
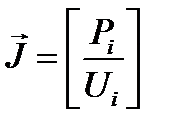
Подставим выражение в выражение:
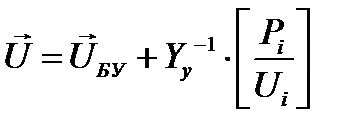
Обратную матрицу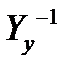 
в выражении обозначим через Z. Она носит название матрицы собственных и взаимных сопротивлений. Элементы матрицы узловых сопротивлений Zij представляют собой коэффициенты частичного падения напряжения, или коэффициенты влияния тока нагрузки в j-том узле на напряжение в i-том узле.
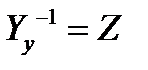
С учетом нового обозначения, уравнение примет вид:
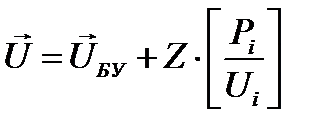
Итерационная процедура определения напряжения по обращенным уравнениям может быть ускорена, если на k-той итерации для расчета i-того неизвестного принимать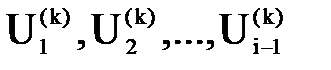 
из этой же k-той итерации, а остальные неизвестные Ui+1 брать из (k-1) итерации, то есть вести процесс по методу ускоренной итерации.
На основе уравнения составим систему уравнений для итерационного процесса:
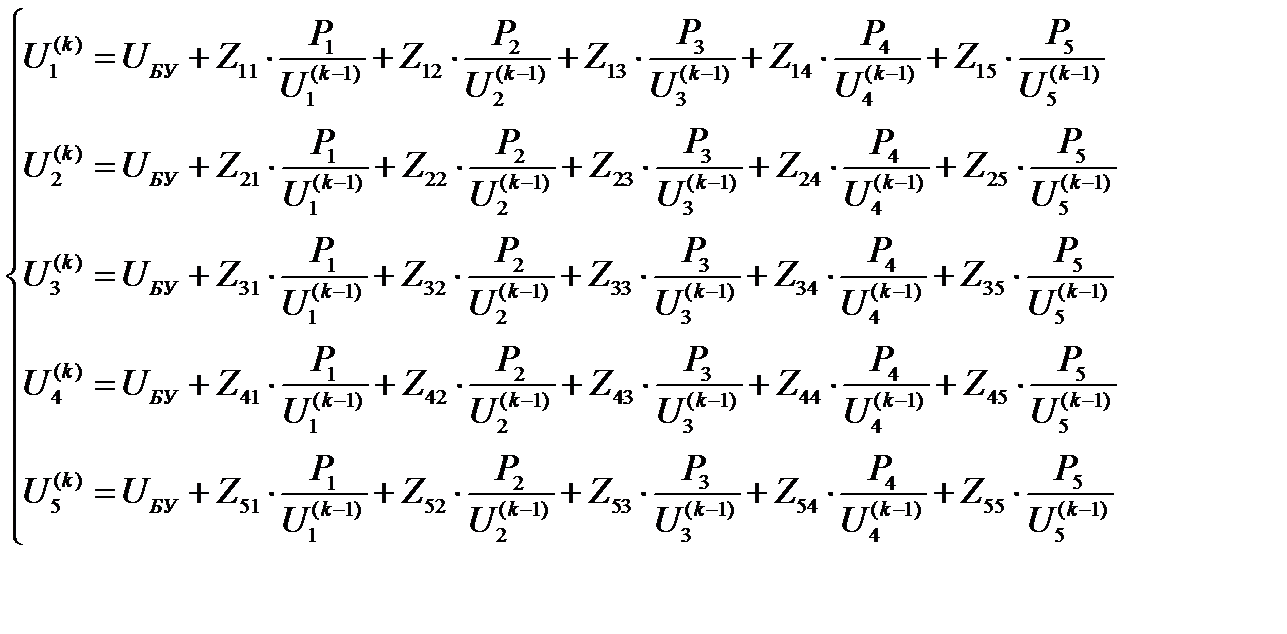
Итерационный процесс необходимо повторять до тех пор, пока не будет удовлетворена заданная степень точности:
где i – номер итерации.
В курсовой работе расчет ведется с применением навыков алгоритмизации, полученных из курса «Информатики». Подпрограмма предусматривает вплоть до 50 итераций, но в случае, если на более ранней стадии будет удовлетворяться заданная степень точности, расчет автоматически прекратится. В качестве напряжения нулевого приближения принимается напряжение балансирующего узла:
Uб=116 В
Для корректной работы подпрограммы достаточно напряжения балансирующего узла Uб, матрицы инциденций М, нагрузки, заданной в мощностях P,и матрицы сопротивлений ветвей ZВ, размерностью AxA, по диагонали матрицы находятся сопротивления ветвей, а все остальные элементы нулевые. (А – число ветвей и хорд исследуемого участка сети).
|
Итерационный процесс заканчивается по достижении шестой итерации. Ниже приведена матрица, состоящая из значений напряжений полученных на каждой из итераций.. В строках указываютсянапряжения в узлах, а в столбцах напряжения, полученные в результате выполнения соответствующих итераций.
Определяем падение напряжения в узлах относительно балансирующего:
|
|
|
Далее по рассчитанным падениям напряжения в ветвях схемы определяем токи в ветвях:
|
| кА |
Определяем падения напряжения в ветвях схемы:
|
|
| кВ |
Определяем потоки мощности в ветвях схемы:
|
|
| МВт |
Определим потери мощности в ветвях сети:
|
МВт
Определяем суммарные потери мощности в ветвях:
|
| МВт |
Определим токи в узлах схемы (кА):
|
|
Определим мощности в узлах сети (МВт):
|
|
Рассчитаем небаланс мощности (%). Как уже говорилось ранее, он не должен превышать 1%.
|
|
|
|
Как видно, небаланс мощности менее 1%. Это свидетельствует о том, что заданная точность итерационного процесса нас полностью удовлетворяет.
Данные потокораспределения приведены на рисунке 4.
|
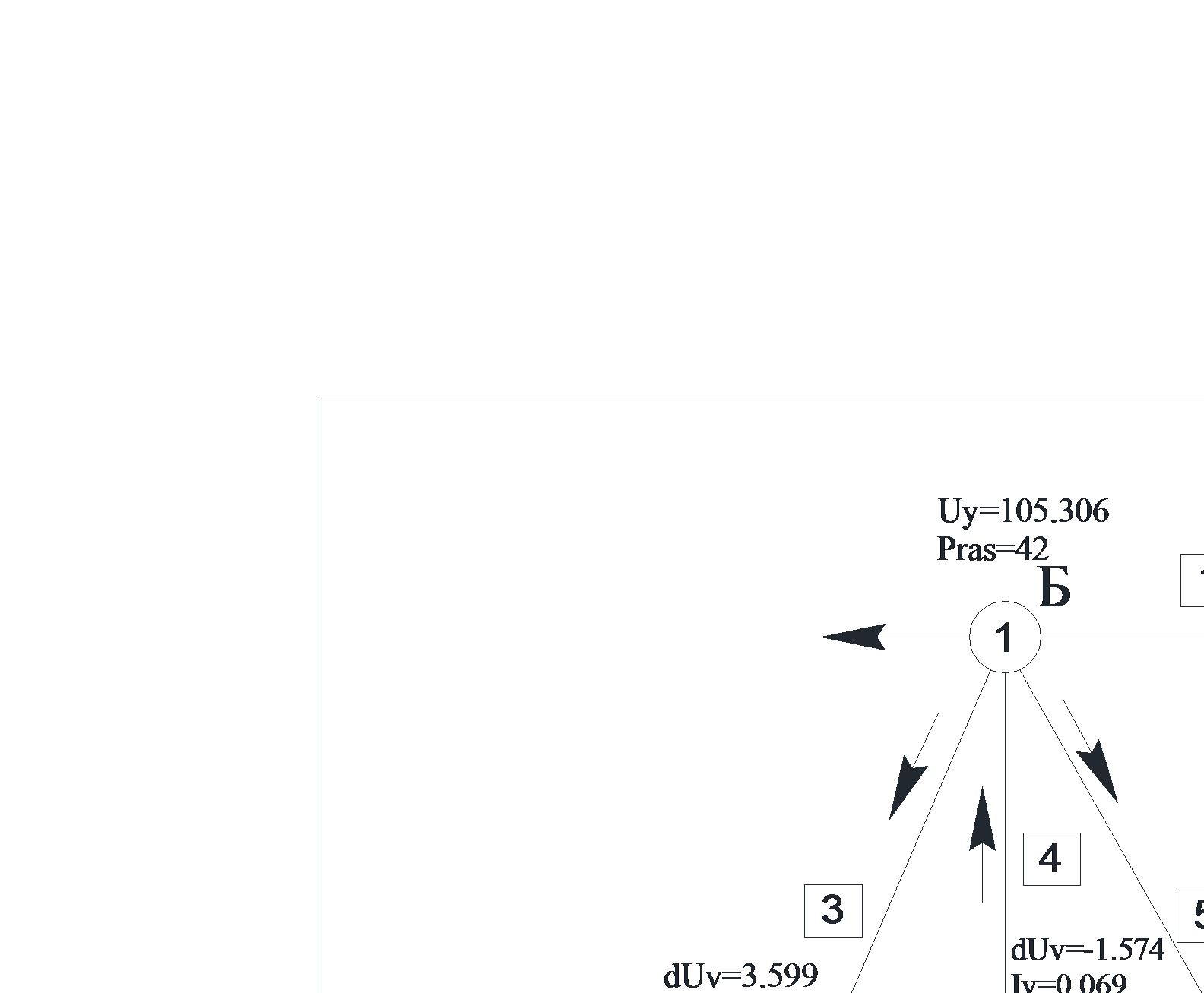
рисунок 4.