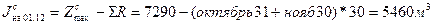Задача 2
Задача. Требуется изготовить: изделий А - 3750 шт.; Б - 4620 шт.; В - 4800 шт., Г - 6600 шт.' д - 1800 шт.; Е •-1980 шт
Указанные изделия можно изготовить на четырех предприятиях, входящих в состав
корпорации, обладающих различной мощностью и различными затратами на изготовление одного изделия.
в табл. 1 приведена мощность предприятий
таблица 1
| . предприятия | Выпуск изделий в смену штук | Эффективный фонд рабочего времени, смен | |||||
| А | Б | В | г | д | Е | ||
| 690 | |||||||
в табл.2 приведены затраты на изготовление одного изделия на каждом предприятии Таблица 2 затраты на изготовление, грн
|
Необходимо составить план производства продукции корпорацией таким образом, чтобы суммарные затраты на и зготовление были минимальными.
решение. В качестве эталона принимается наиболее мощное 3 предприятие и присваивается ему коэффициент мощности, равный I {К, = I). Коэффициенты мощности остальных предприятий вычисляется как отношение мощности (объема выработки продукции в смену) i-го предприятия к мощности эталонного предприятия. Они приблизительно равны:
к1= 10/15=15/22=8/12=20/30=4/6=2/3
к2= 5/15=7/23/4/12=10/30=2/6=1\3
к3= 7\15=11/22=6/12=15/30=3\6=1\2
Па основании коэффициента мощности вычисляются приведенные фонды рабочего времеии предприятий-изготовителей (в приведенных сменах умножением действителнього фонда рабочего времени i-го предприятия (а1) на коэффициент его мощности К1).
для 1-го предприятии: 600х 2/3 = 400 приведенных смен:
2-го 690х 1/3 = 230 пр. см.;
3го 580 х 1 = 580 нр. см.;
4-го 720 х 1\2= 360 пр. см.
Итого 1570 приведенных смен
Программа производства изделии также выражается через количество приведенных смен рабочего времени которое необходимо затратить на их изготовление, Для этого план производства j-г'о продукта делится на количество j-ой' продукции. производимой в смену на эталонном предприятии:
А = 3750+15 = 250 приведенных смен;
Б= 4620+22 = 210 пр. см.
В= 4800+12 = 400 пр. см.:
Г = 6600+30 = 220 нр. ем.:
Д =1800+б = 300 пр. см:
Е = 1980+18 = 110 нр. см. '
Итого 1490 приведенных смен.
Из расчетов видно, что ресурсы приведенных смен превышаю! потребность в них на 1570 - 1490 = 80 приведенных смен, следовательно, эго отккрытая Т-задача, для решения, которой следует ввести фиктивное изделие (Ф), на изготовление которого следует затратить 80 приведенных смен. 1,;
в табл. 3 представлено базисное распределение изделии по предприятиям- ’ изготовителям, составленное методом «наименьшей стоимости» В углах квадратов вместо транспортных расходов указаны затраты на изготовление изделия, взятые из табл. 2. Для фиктивного изделия устанавливается максимальная себестоимость, равная 10 UAН.
таблицаЗ
базисное распределение продукции
| предприятия | изделия | ресурсы (приведенные смены) | ||||||
| а | б | В | Г | д | е ф | |||
| **2 | ||||||||
| *3 | **2 | i0 | ||||||
| *2 | * * 1 | 8о | ||||||
| *2 | **1 | |||||||
| Спрос (привед смены) |
| В таблю 4 представлено базисное решение задач с рассчитанными потенциалами и проверкой на оптимальность. |
| изделия | а б | в | Г | Д | е | ф | Ресурсы (приведенные смены) | ||
| предприятия | Vj Ui Ui | -I | _2 | ||||||
| К) | |||||||||
| -3 | + 3 | -2 23() | * | ||||||
| -3 | -7 | + 2 170 | |||||||
| 1 10 | |||||||||
| Спрос (привел, смены) | 1 10 |
из табл. 4 видно. что не выполняется условие оптимальности для квадрата Б-2 и Ф-2, в наибольшей степени оно не выполняется для квадрата Б-2 (-3 + 3 = 0 < 4) Д = 4, а для квадрата Ф-2 дельта = 1, следовательно, оптимизировать необходимо квадрат Б-2.
Для этого осуществляют перемещение но свяэке, как это укачано в габл. 2.4, Перемещают наименьшее число приведенных смен со знаком минус, т.е. 60 смен. После перестановки получают первую итерацию, отображенную в табл. 5.
Таблица 5
первая итерация
| изделия | А | б | В | Г | Д | е | ф | Ресурсы (приведенные смены) | |
 Предприятия1 Предприятия1
| Vj Ui | ||||||||
| I | -4 | 5" | +10 | ||||||
| +3 | 10 | ||||||||
| +2 | - 10 | ||||||||
| 1 10 | |||||||||
| Спрос(принсл СМСнм) | 400 220 |
Как видно из табл. 5, условие оптимальности не выполняется для квадрата Ф-1 (0 + 10 = 10 < 11, дельта=1. это значит, что. переместив в данный квадрат какое-то распределение, можно получить план изготовления с меньшими затратами.
| изделия а | б | в | Г | Д | е | Ф | ресурсы (приведенные смены) | ||
| предприятия | Vj Ui | ||||||||
| 1 10 | |||||||||
| Спрос (приведенные смены) |
Перемещают наименьшее число приведенных смен со -знаком минус,т.е. 80 смен из кdадрата (Ф-3. После перестановки получают вторую итерацию, изображенную в табл. 6, в которой все свободные квадраты выполняют условие оптимальности/
| таблица.6 |
| вторая итерация |
| .... |
 нa основании табл. 6 определяется количество изделий, которое должно производить каждое предприятие при условии, что суммарные затраты па изготовление изделий в заданной номенклатуре будут минимальные. ‘
нa основании табл. 6 определяется количество изделий, которое должно производить каждое предприятие при условии, что суммарные затраты па изготовление изделий в заданной номенклатуре будут минимальные. ‘
В табл. 6 распределение изделий по предприятиям выражено в приведенных сменах, т е в сменах эталонного предприятия. Для того, чтобы эти смены перенести в конкретные изделия, необходимо число смен умножить на количество данного изделия производимого в смену эталонным предприятием (табл. 7).
, Таблица 7
количество изделий производимом на каждом предприятиипри оптимальном распределении
|
Из табл. 6 видно, также, что у первого предприятия остаются незагруженными 80 приведенных смен (время, предусмотренное для и п отопления фиктивного изделия), т.е.: 80/(2/3) =120 действительных смен, которые можно использовать для изготовления непредусмотренной планом продукции.
Логистика запасов
Задача1.
Затраты на поставку единиц продукции – 12,75 UAN; годовое потребление 1000 ед.; затраты на хранение единицы продукции 0,1 UAN. Размер партии поставки 100; 200; 400; 500; 600; 800; 1000 ед.
Рассчитать:
1) Оптимальный размер закупаемой партии.
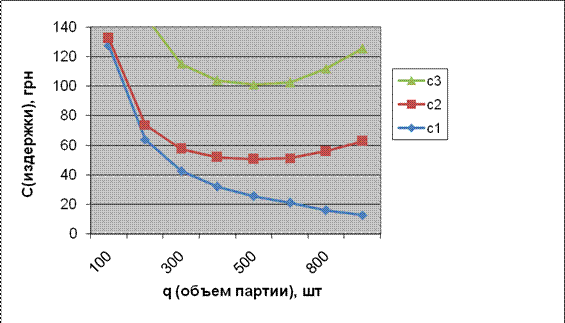
2) Построить график суммарных годовых издержек, связанных с образованием и хранением запасов.
Решение:
Q=1000 ед.
C1=12,75 грн/ед
С2=0,1 грн/ед
qn -?
g= qn = 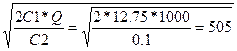 ед.
ед.
С100= 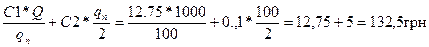 (127,5-С1; 5=С2, 132,5=С3)
(127,5-С1; 5=С2, 132,5=С3)
С200= 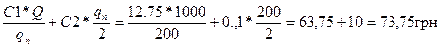
С300= 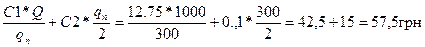
С400= 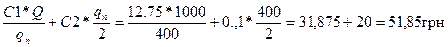
С500 = 
С600= 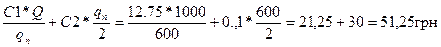
С800= 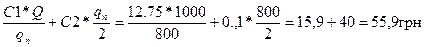
С1000= 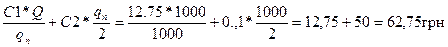
Задача 2.
Лесопильный завод получает лес в период с 01.06 по 0,.10. Программа производства 10950м2, годовой фонд рабочего времени – 365 суток. Определить величину сезонного запасп: максимальную и на 01.12, 01.04, 01.06.
Решение:
1) Определим среднесуточное потребление леса:

2) Определим величин максимального сезонного запаса:
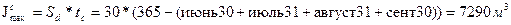
3) величина сезонного запаса на любую дату года: