Практическая работа № 2
Тема: «Арифметические операции в системах счисления».
Цели:Углубить и расширить знания о переводе чисел из одной системы счисления в другую, об арифметических действиях в разных системах счисления
Ход работы:
Кодирование информации
Кодирование информации – это операция преобразования информации из одной знаковой системы в другую.
Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. Например, при вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на компьютере, происходит кодирование знака, т.е. преобразование его в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс – декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение.
Двоичное кодирование информации.
Для представления информации в компьютере используется двоичное кодирование, т.к. технические устройства компьютера могут сохранять и распознавать не более двух различных состояний (цифр): намагничен / размагничен (участок поверхности магнитного носителя информации), отражает/не отражает (участок поверхности лазерного диска); и т.д.
Информация на компьютере представлена в машинном коде, алфавит которого состоит из цифр (0 и 1). Каждая цифра машинного кода несет информацию в 1 бит.
Системы счисления
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемыми цифрами.
Различные системы счисления могут отличаться друг от друга по следующим признакам:
· разное начертание цифр, которые обозначают одни и те же числа;
· разные способы записи чисел цифрами;
· разное количество цифр.
По способу записи чисел цифрами системы счисления бывают: позиционные и непозиционные.
Непозиционная система счисления – система, в которой значение символа не зависит от его положения в числе.
В римской системе счисления для обозначения чисел используются заглавные латинские буквы, являющиеся «цифрами» этой системы счисления:
| I | V | X | L | C | D | M |
Число в римской системе счисления обозначается набором стоящих подряд «цифр». Значение числа равно:
1) сумме значений идущих подряд нескольких одинаковых «цифр» (назовем их группой первого вида);
2) разности значений большей и меньшей «цифр», если слева от большей «цифры» стоит меньшая (группа второго вида);
3) сумме значений групп и «цифр», не вошедших в группы первого и второго видов.
Примеры.
1. Число 32 в римской системе счисления имеет вид:
XXXII = (X+X+X)+(I+I) =30+2 (две группы первого вида)
2. Число 444 в римской системе счисления имеет вид:
CDXLIV = (D-C)+(L-X)+(V-I) (= 400 + 40 + 4 – три группы второго вида)
3. Число 1974:
MCMLXXIV = M+(M-C)+L+(X++X)+(V-I) = 1000+900+50+20+4 (наряду с группами обоих видов в формировании числа участвуют отдельные «цифры»)
4. Число 2005:
MMV = (M+M) +V = 1000+1000+5 (две группы первого вида)
Позиционная система счисления – система, в которой значение символа зависит от его места в ряду символов (цифр), изображающих число. Каждая позиционная система счисления имеет определенный алфавит цифр и основание, равное количеству цифр (знаков в ее алфавите).
Позиционные системы счисления более удобны для вычислительных операций, поэтому они и получили наибольшее распространение.
Основанием позиционной системы счисления называется возводимое в степень целое число, которое равно кол-ву цифр, используемых для изображения чисел в данной системе счисления.
Наименование системы счисления соответствует ее основанию (например, десятичной называется система счисления так потому, что ее основание равно 10, т.е. используется десять цифр).
| Система счисления | Основание | Количество цифр | Цифры |
| двоичная | 0,1 | ||
| троичная | 0,1,2 | ||
| восьмеричная | 0,1,2,3,4,5,6,7 | ||
| десятичная | 0-9 | ||
| шестнадцатеричная | 0-9,А,В,С,D,E,F |
Из курса математики вам известно, что любое натуральное число в десятичной системе счисления можно представить в виде конечной суммы степеней числа 10 с коэффициентами, равными соответствующим десятичным цифрам натурального числа:
 |
Развернутой формой записи числа называется такая запись: а4а3а2а1а0 = а4*q4 + a3*q3 + a2*q2 + a1*q1 + a0*q0, где а4,а3,а2,а1,а0 –цифры числа, q –основание степени.
Таблица соответствия систем счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| А | |||
| В | |||
| С | |||
| D | |||
| Е | |||
| F | |||
| … | … | … | … |
| 1А |
Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:
- Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
- Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
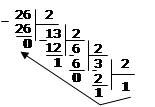Пример. Перевести 2610 в двоичную систему счисления. А10→А2
Решение:
Ответ: 2610=110102
Пример. Перевести 362710 в шестнадцатеричную систему счисления. А10→А16
Решение:
Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16.
Ответ: 362710=E2B16
Правило перевода дробных чисел из десятичной системы счисления в систему с основанием q:
- Последовательно выполнять умножение исходного числа и получаемых дробные части на q до тех пор, пока дробная часть не станет равна нулю или не достигнем требуемую точность.
- Полученные при таком умножении целые части - числа в системе счисления q – записать в прямом порядке (сверху вниз).
Пример. Перевести 0,562510 в двоичную систему счисления. А10→А2
Ответ: 0,562510 = 0,10012
Правило: Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.
Пример. Перевести число 1101102 из двоичной системы счисления в десятичную.
Решение:
5 4 3 2 1 0
1 1 0 1 1 0 2 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20 =32+16+4+2=5410
Ответ: 1101102 = 5410
Пример. Перевести число 101,012 из двоичной системы счисления в десятичную.
Решение:
2 1 0 -1 -2
1 0 1,0 1 2 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510
Ответ: 101,012 = 5,2510
Пример. Перевести число 234,68 из восьмеричной системы в десятичную:
Решение:
2 1 0 -1
2 3 4, 68 = 2*82 +3*81 + 4*80 +6*8-1= 2*64+3*8+4+6*0,125= 128+24+4+0,75 =156,7510
Ответ: 234,68 = 156,7510.
Пример. Перевести число 2Е16 в десятичную систему счисления.
Решение:
2 1
2 Е16 = 2*161 +14*160 = 32 +14 = 4610.
Ответ: 2Е16 = 4610 .
Правило Чтобы перевести целое двоичное число в восьмеричную (8=23) систему счисления необходимо:
· разбить данное число справа налево на группы по 3 цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления.
Пример. Перевести число 111010102 в восьмеричную систему счисления.
Решение:
11101010
3 5 2
Ответ: 111010102 = 3528
Правило Чтобы перевести целое двоичное число в шестнадцатеричную (16=24) систему счисления необходимо:
· разбить данное число справа налево на группы по 4 цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления.
Пример. Перевести число 111000102 в шестнадцатеричную систему счисления.
Решение:
Е 2
Ответ: 111000102 = Е216
Правило Чтобы перевести дробное двоичное число в восьмеричную (шестнадцатеричную) систему счисления необходимо:
· разбить данное число, начиная от запятой влево целую часть и вправо дробную часть на группы по 3 (4) цифры в каждой;
· рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной (шестнадцатеричной)системы счисления.
Пример. Перевести число 111100001,01112 в восьмеричную систему счисления.
Решение:
111100001,0111
7 4 1 3 1
Ответ: 111100001,01112= 741,318
Правило Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления.
Пример. Перевести число 5288 перевести в двоичную систему счисления.
Решение:
5 2 3
101 010 011
Ответ: 5288 = 1010100112
Пример. Перевести число 4ВА35,1С216 перевести в двоичную систему счисления.
Решение:
4 В А 3 5, 1 С 2
100 1011 101000110101 0001 1100 0010
 |
Ответ: 4ВА35,1С216 = 10010111010001101010001 110000102
Арифметические операции в двоичной и кратных ей системах счисления.
Арифметические операции в позиционных системах счисления производится по единому алгоритму. Так, сложение двоичных чисел происходит по классическому алгоритму «столбиком» с переносом числа, кратного двум, единицей в следующий разряд.
Рассмотрим этот алгоритм на примере двух двоичных чисел 10101012 и 1101112:
| Дописывание единицы | ||||||||
| Первое слагаемое | ||||||||
| Второе слагаемое | ||||||||
| Сумма |
Результат сложения выглядит как 100011002. Проверим результат сложения, для чего переведем все числа в десятичную систему счисления:
10101012=8510, 1101112=5510, 100011002=14010, 8510+5510=14010.
Двоичная система, являющаяся основой компьютерной арифметики, весьма громоздка и неудобна для использования человеком. Поэтому программисты используют две кратные двоичной системы счисления: восьмеричную и шестнадцатеричную. В случае шестнадцатеричной системы арабских цифр не хватает, и в качестве цифр используются первые шесть заглавных букв латинского алфавита.
При выполнении заданий на сложение чисел разных систем счисления их нужно перевести в одну систему счисления. Лучше всего пользоваться той системой, в которой должен быть представлен результат.
Пример. Вычислите значение суммы в десятичной системе счисления:
102+108+1016 =?10
Решение. Переведем все числа в десятичную запись:
102+108+1016 = (1*21+0*20) + (1*81+0*80) + (1*161+0*160) = 2+8+16=2610. Ответ: 26.
Пример. В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе?
Решение.
11112=1*23+1*22+1*21+1*20→8+4+2+1=1510.
11002=1*23+1*22+0*21+0*20→8+4=1210
1510+1210=2710
Ответ: в классе 27 учеников.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
Проверку выполнения заданий осуществите с использованием программы Калькулятор.
1. 
Программа запускается командой Пуск 4 Программы4Стандартные4Калькулятор.
2. Окно программы выглядит точно так же, как реальный электронный калькулятор. Вводить данные можно, щелкая на кнопках или нажимая соответствующие клавиши. При включенном режиме NUM LOCK можно вводить цифры с помощью дополнительной панели клавиатуры.
3. Для работы в разных системах счисления программа Калькулятор должна быть переведена в режим ПРОГРАММИСТ. Другие системы счисления поддерживаются только при работе с целыми числами. Максимально возможный размер такого числа – 4 байта (восемь шестнадцатеричных цифр).
4. Выбор системы счисления осуществляется при помощи группы переключателей – Нех (шестнадцатеричная), DEC ( десятичная), OCT (восьмеричная), BIN( двоичная). При установке одного из этих переключателей остаются (или становятся) активными только те цифровые кнопки, которые соответствуют цифрам, возможным в данной системе счисления. Кнопки с буквами A-F соответствуют цифрам шестнадцатеричной системы.
5. Если ввести число в одной системе счисления, а затем установить переключатель, соответствующий другой системе счисления, то число на индикаторе автоматически переводится в другую систему.
6. Благодаря этому, вычисления с использованием чисел, записанных в разных системах счисления, идут гладко. Можно использовать в операциях числа в разной системе счисления, если только не забывать вовремя, устанавливать переключатель нужной системы. После того как получен окончательный результат, его также можно преобразовать в другую систему счисления.
Таблица. Назначение кнопок калькулятора.
| Кнопка | Назначение кнопки | Кнопка | Назначение кнопки |
| Удаление последней цифры числа | 
| Копирование числа из поля ввода текста в память |
| Удаление введенного числа из поля ввода текста | 
| Суммирование числа, записанного в памяти, и числа, находящегося в поле ввода текста. |
| Начало вычислений по новой формуле | 
| Деление |
| Очистка памяти | 
| Умножение |
| Замена числа в поле ввода текста числом, записанном в памяти | 
| Вычитание |
| Суммирование |
Вариант №1
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
 10 2, 8, 16
|  2 8, 16
| 8 2
|  2, 8, 16 10
| ||
| 25610 | 721,618 | 10010102 | 2916 1D16 | 11001101+11011 | |
| 12510 | 775,118 | 775,118 | 138 716 | 1001*101 | |
| 24,3210 | 11101,111 | 2058 | 294,316 | 2316 418 | 125,358*25,478 |
Вариант №2
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
|  16 2
|  2, 8, 16 10
| ||
| 35410 | 11110002 | 294,316 | 100111100,11012 | 118 616 | 1010101 + 10000101 |
| 0,2410 | 11110000002 | 51А416 | 1233,58 | 558 111012 | 11001 * 1011100 |
| 1,2510 | 111101100,011012 | 2B3,F416 | 2В3,F416 | 4158 23B416 | 451,28 * 5,24 8 |
Вариант №3
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 8 2
|  2, 8, 16 10
| ||
| 2510 | 10010101002 | 324,658 | 10110101,12 | 293,816 3CC,9816 | 1111011101 + 101101000 |
| 7510 | 1001111101112 | 671,248 | 2001,68 | 24108 1101102 | 1011001 * 1011011 |
| 71,2510 | 1001011110,0112 | 24108 | 2C,416 | 125,28 12,9816 | 2B,A16 * 36,616 |
Вариант № 4
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 16 2
|  2, 8, 16 10
| ||
| 8610 | 10011012 | 41A,616 | 10011100112 | 1723,28 15,28 | 110111011+110110110 |
| 7810 | 100110010112 | 2C,416 | 1723,28 | 1000012 278 | 110010*101110 |
| 91,6210 | 1110101,00110112 | 4AC16 | 54,316 | 30748 258 | 356,58 + 1757,048 |
Вариант №5
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8,16
| 2 8, 16
| 8 2
|  2, 8, 16 10
| ||
| 27310 | 10010101002 | 632,28 | 11000000002 | 4F816 1816 | 1100100012+10011012 |
| 66110 | 1011011110112 | 141,348 | 347,28 | 573,048 18,816 | 110112 *11102 |
| 26,7810 | 1001000011,12 | 348 | 10,A816 | 10102 41208 | AF16 + 9 7 16 |
Вариант №6
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 16 2
|  2, 8, 16 10
| ||
| 21810 | 11010100012 | FA,716 | 11011111002 | 714,348 133,48 | 1110100102+10110111102 |
| 80810 | 1000111002 | 155,6C16 | 415,248 | 16,B16 54568 | 10111002* 11001002 |
| 156,2510 | 10101001,12 | 1E16 | E5,416 | 100012 338 | 158,A16 + 34,C16 |
Вариант №7
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8,16
| 2 8, 16
| 8 2
| 2, 8, 16 10
| ||
| 10010 | 11110001112 | 478 | 1000001111,012 | 465,38 252,3816 | 11110002 + 111111112 |
| 5710 | 110101012 | 1347,178 | 465,38 | 2DB,616 15E,616 | 1100102 * 1011102 |
| 176,2510 | 1001111010,0100012 | 53608 | 239,A16 | 11011012 9C,416 | 520,48 + 635,48 |
Вариант №8
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8,16
| 2 8, 16
| 16 2
| 2, 8, 16 10
| ||
| 20310 | 11011012 | 6,516 | 1101001010,1012 | 1E5,1816 3BA,7816 | 10111012 + 111111012 |
| 18410 | 1111110002 | 367,3816 | 704,68 | 102,28 55,416 | 101101 * 110011 |
| 218,510 | 1011101011,0012 | AF016 | 2DE,616 | 11102 1C16 | 1E5,1816 + 3BA,7816 |
Вариант №9
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 8 2
|  2, 8, 16 10
| ||
| 30610 | 10001101102 | 666,168 | 110010010,1012 | 666,168 1C7,6816 | 10100002 +10110012 |
| 19110 | 1111000012 | 575,28 | 605,028 | 10010102 102,28 | 100011 * 100111 |
| 667,2510 | 1110010100,10112 | 1053,348 | 3C8,816 | 84,816 27E,816 | 242,28 + 1153,58 |
Вариант №10
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 16 2
|  2, 8, 16 10
| ||
| 52410 | 1011111112 | 1DE,5416 | 1111100100,112 | 1110002 1001112 | 10000102 + 1110102 |
| 22210 | 11111001102 | 1716 | 140,228 | 1476,38 D6316 | 1110002 * 1001112 |
| 318,8710 | 1110001101,10012 | 40A,E816 | 1DE,5416 | 101000102 16310 | 157,48 + 3E0,A16 |
Вариант №11
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8,16
| 2 8, 16
| 8 2
| 2, 8, 16 10
| ||
| 11310 | 111010002 | 1600,148 | 1101101000,012 | 177,48 23,48 | 101100112 +1110102 |
| 87510 | 1053,348 | 1600,148 | 100002 10,616 | 11001102* 1100102 | |
| 6,5210 | 1101101000,012 | 135,288 | 1E9,416 | 11910 81,A16 | 348,116 + 234,416 |
Вариант №12
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 16 2
|  2, 8, 16 10
| ||
| 29410 | 100000110012 | 200,616 | 1101100,012 | 1111012 77,248 | 1110112 +100101102 |
| 72310 | 101011002 | 81,A16 | 1053,28 | 631,18 263,28 | 1111012 * 11112 |
| 950,2510 | 1101100,012 | 37D,416 | 8F616 | 1D6,8816 53,2610 | 104,48 + 1310,628 |
Вариант №13
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 8 2
| 2, 8, 16 10
| ||
| 61710 | 1101111012 | 1471,178 | 10010110,10112 | 423,12510 4A,416 | 111010102 +1110102 |
| 59710 | 11100111012 | 750,168 | 1017,38 | 712,38 64,28 | 10011012 * 11100012 |
| 84,8210 | 111001000,012 | 1345,348 | 1D4,C816 | 1010002 238 | 346,416 + 33F,A16 |
Вариант №14
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 16 2
| 2, 8, 16 10
| ||
| 104710 | 1000010102 | 1E7,0816 | 1011010101,12 | 274,58 31,348 | 111000012 +1110112 |
| 33510 | 11111011112 | 2E9,216 | 452,638 | 74,510 1416 | 11011112 * 10000102 |
| 814,510 | 1011010101,12 | 92,716 | 13,416 | 111001012 24,416 | 1672,28 + 266,28 |
Вариант №15
| Перевести из одной системы в другую | Сравнить два числа | Выполните действия | |||
| 10 2, 8, 16
| 2 8, 16
| 8 2
|  2, 8, 16 10
| ||
| 88710 | 10101000012 | 247,18 | 1000001101,012 | 44,816 13,616 | 11110112 +10110002 |
| 23310 | 11111011112 | 1711,68 | 1567,28 | 67,416 57,148 | 1111002 * 11010012 |
| 801,510 | 1000001101,012 | 33168 | 44,816 | 100102 278 | 156,9816 + D3,216 |
Выполненную и правильно оформленную работу предоставить преподавателю.