Цели занятия:
Обобщение и систематизация знаний учащихся по теме «Функции, их свойства и графики», закрепление определений свойств функций, выработка навыков исследования функций.
Задачи занятия:
Образовательная – обобщение знаний учащихся по теме «Функции, их свойства и графики», совершенствование знаний о числовых функциях путем введения точных определений их свойств.
Развивающая – развитие и совершенствование умения работать с различными источниками информации; анализировать, сравнивать, работать с таблицами, графиками, развитие внимания, наблюдательности, памяти, логического мышления учащихся через формирование строить графики функций.
Воспитательная – воспитание познавательной активности, интереса к изучению математики, формирование исследовательских умений, математической и графической культуры учащихся.
Тип урока: комбинированный урок совершенствования знаний, умений и навыков.
Оснащение урока: Башмаков М.И. «Математика» - учебник для начального и среднего профессионального образования; Башмаков М. И. «Математика» - книга для преподавателя (методическое пособие); ТСО: компьютер, проектор, экран, презентация к уроку PowerPoint, доска, маркеры,
схема исследования функций, раздаточный дидактический материал, калькуляторы.
Формы работы: фронтальная, парная, самостоятельная.
Методы обучения: репродуктивный, информационно-рецептивный, частично-поисковый.
План занятия:
1.Организационный момент: Обсуждение темы и формулирование целей урока.(2-3минуты)
2.Проверка домашнего задания .(5-6минут)
3.Основной этап. (75 минут)
3.1.Устная работа.
3.2.Изучение нового материала. Примеры зависимостей между переменными в реальных процессах и явлениях.
3.3.Решение задач на построение и чтение графиков функций.
3.4.Контроль.
4.Заключительный этап. (5-6 минут)
4.1.Домашнее задание.
4.2.Итоги урока. Рефлексия. Оценки.
Ход занятия:
1.Преподаватель обсуждает с учащимися тему и формулируют цель занятия и средства ее достижения.
2. Преподаватель выясняет, правильно ли учащиеся выполнили домашнее задание.
З.Основной этап.
3.1.Повторение. Учащиеся отвечают на вопросы:
Слайд 4
1) Верно ли утверждение:
а) функция y = 2x возрастает на области ее определения;
б) функция y = -5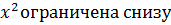 
;
в) функция y =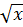 
выпукла вниз;
г) для функции y =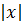 
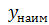не существует;
2) Найдите область определения функции:
а) 
3) Найти область значений функции:
а) y =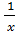 
б)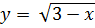 
3.2. Изучение нового материала. Примеры зависимостей между переменными в реальных процессах и явлениях.
Давайте вспомним, сколько вокруг нас действует законов: физических, юридических, моральных и многих других. Их незнание может привести к нежелательным, негативным последствиям. Знание же законов бывает очень полезным.
Допустим, человек тренируется бросать мяч в корзину с определенного места баскетбольной площадки, но мяч не долетает до корзины. Что нужно сделать? Правильно – увеличить силу броска. Игрок интуитивно пользуется физическим законом: чем с большей силой воздействовать на объект перед началом движения, тем большей будет его скорость и дальность перемещения.
Хозяйка видит растение, у которого начинают засыхать листья. Что она предпримет? Скорее всего польет корни. Причем поливать она будет корни, а не пожелтевшие листья. Все потому, что хозяйка знает биологический закон: питательные вещества и влага добываются корнями растения из почвы и поднимаются вдоль по стволу наверх.
Знание закона помогает предугадать последующие события. Но интуитивное применение законов приводит лишь к приблизительному угадыванию результата. Но сколько есть ситуаций, когда пробы и ошибки не допустимы. Вспомним поговорку: «Сапер ошибается только один раз». А хирурги, фармацевты, водители, авиаконструкторы, физики – атомщики!
Вот тут – то и помогает математическое выражение данного закона или взаимосвязи. При выполнении некоторых условий запись закона языком математики и будет функцией.
Преподаватель предлагает ответить на вопросы, используя знания о свойствах функций.
Свойства практических зависимостей.
Является ли монотонной функция, выражающая зависимость:
1) Массы человека от его роста;
2) Стоимости проезда на метро от протяженности маршрута;
3) Успехов футбольной команды от стоимости ее игроков;
4) Массы железного шарика от его объема;
5) Расстояния от поверхности земли прыгуна в высоту во время прыжка?
Является ли непрерывной функция, выражающая зависимость:
1) Стоимости проезда на пригородном поезде от пройденного им расстояния;
2) Показания электросчетчика от времени;
3) Массы мотка проволоки от ее длины?
Является ли периодическим следующее явление:
1) Океанский прилив;
2) Восход солнца;
3) Извержение гейзера;
4) Олимпийские игры;
5) Сокращение сердечной мышцы?