т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В.
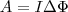
значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение (6) верно для контура любой формы в произвольном магнитном поле.
Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна 
где I — сила тока в контуре.
Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна
БИЛЕТ 14. Система уравнений Максвелла в интегральной форме и физический смысл входяших в нее уравнений.
1) 
2) 
3) 
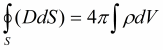
4) 
Сформулируем основные выводы (физический смысл), следующие из уравнений Максвелла:
1. Всякое изменение во времени электрического или магнитного поля приводит к возникновению соответственно вихревого магнитного или вихревого электрического поля. Независимое существование друг от друга переменных электрических и магнитных полей невозможно, они непрерывно переходят одно в другое.
2. Независимое существование электрических и магнитных полей возможно только в случае статических (неподвижных) зарядов и постоянных магнитов.
3. Силовые линии электрического поля могут иметь истоки и стоки (закон существования электрического заряда), тогда как силовые линии магнитного поля всегда непрерывны, т.е. замыкаются на себя (закон отсутствия магнитного заряда).
4. Источниками электрического поля являются заряды и токи, поэтому электрическое поле может быть как потенциальным (заряды), так и вихревым (токи).
5. Источниками магнитного поля являются движущиеся заряды (токи проводимости) или возмущение электрического поля (ток смещения), поэтому магнитное поле всегда имеет вихревой характер.
БИЛЕТ 15. Идеальный гармонический осциллятор. Уравнение идеального осцилятора и его решение. Амплитуда. частота и фаза колебания. Энергия колебаний. Примеры колебательных движений различной физической природы.
Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука): 
, где k — коэффициент жёсткости системы.
Общее решение уравнения записывается в виде: 
где амплитуда A и начальная фаза φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости).Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой
Амплитуда - величина наибольшего отклонения системы от положения равновесия. 
- круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса 
- называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φпредставляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π/ .
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота = 2π/T = 2πν дает число колебаний за 2π секунд.
Кинетическая энергия
Кинетическая энергия физической системы, совершающей гармонические колебания, 
, где скорость v изменяется по гармоническому закону,v = - wA sin(wt + jo).
удобнее представить в следующем виде:
Вывод: Кинетическая энергия физической системы также совершает гармонические колебания с круговой частотой 2w, а величина ее периодически изменяется от 0 до mw2A2/2.
Потенциальная энергия
В связи с тем, что любая физическая система, совершающая гармонические колебания, имеет общий вид дифференциального уравнения, то на такую систему действует квазиупругая сила(похожая по действию на упругую силу, но по природе не являющаяся упругой). Поэтому потенциальную энергию колеблющейся системы найдем по формуле потенциальной энергии упруго деформированной пружины: 
после подстановки для потенциальной энергии, получим выражение 
Полная механическая энергия физической системы, совершающей механические колебания 
| Примеры колебаний различной физической природы: -механические — математический маятник, пружины с грузом -упругие — звук - электрические — переменный ток -электромагнитные - Простейшая система, в которой могут происходить свободные электромагнитные колебания, состоит из конденсатора и катушки, присоединённой к его обкладкам. Такая система называется колебательным контуром. |