Квадратное неравенство
Естественно, прежде чем говорить о решении квадратных неравенств, надо отчетливо понимать, что такое квадратное неравенство. Иными словами, нужно по виду записи уметь отличать квадратные неравенства от неравенств других видов.
Определение.
Квадратное неравенство – это неравенство вида a·x2+b·x+c<0 (вместо знака > может быть любой другой знак неравенства ≤, >, ≥), где a, b и c – некоторые числа, причем a≠0, а x – переменная (переменная может быть обозначена и любой другой буквой).
Сразу дадим еще одно название квадратных неравенств – неравенства второй степени. Это название объясняется тем, что в левой части неравенств a·x2+b·x+c<0 находится многочлен второй степени - квадратный трехчлен. Термин «неравенства второй степени» используется в учебниках алгебры Ю. Н. Макарычева, а Мордкович А. Г. придерживается названия «квадратные неравенства».
Также иногда можно слышать, что квадратные неравенства называют квадратичными неравенствами. Это не совсем корректно: определение «квадратичные» относится к функциям, заданным уравнениями вида y=a·x2+b·x+c. Итак, есть квадратные неравенства и квадратичные функции, но не квадратичные неравенства.
Покажем несколько примеров квадратных неравенств: 5·x2−3·x+1>0, здесь a=5, b=−3 и c=1; −2,2·z2−0,5·z−11≤0, коэффициенты этого квадратного неравенства есть a=−2,2, b=−0,5 и c=−11;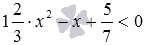 
, в этом случае 
.
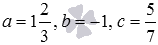Обратите внимание, что в определении квадратного неравенства коэффициент a при x2 считается отличным от нуля. Это и понятно, равенство коэффициента a нулю фактически «уберет» квадрат, и мы будем иметь дело с линейным неравенством вида b·x+c>0 без квадрата переменной. А вот коэффициенты b и c могут быть равными нулю, причем как по отдельности, так и одновременно. Вот примеры таких квадратных неравенств: x2−5≥0, здесь коэффициент b при переменной x равен нулю; −3·x2−0,6·x<0, здесь c=0; наконец, в квадратном неравенстве вида 5·z2>0 и b, и c равны нулю.
Как решать квадратные неравенства?
Теперь можно озадачиться вопросом как решать квадратные неравенства. В основном для решения используются три основных метода:
· графический способ (или, как у А. Г. Мордковича, функционально-графический),
· метод интервалов,
· и решение квадратных неравенств через выделение квадрата двучлена в левой части.
Графическим способом
Сразу оговоримся, что метод решения квадратных неравенств, к рассмотрению которого мы приступаем, в школьных учебниках алгебры не называют графическим. Однако по сути это он и есть. Более того, первое знакомство с графическим способом решения неравенств обычно и начинается тогда, когда встает вопрос, как решать квадратные неравенства.
Графический способ решения квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥) заключается в анализе графика квадратичной функции y=a·x2+b·x+c для нахождения промежутков, в которых указанная функция принимает отрицательные, положительные, неположительные или неотрицательные значения. Эти промежутки и составляют решения квадратных неравенств a·x2+b·x+c<0, a·x2+b·x+c>0, a·x2+b·x+c≤0 и a·x2+b·x+c≥0 соответственно.
Разбор всех тонкостей этого способа, соответствующий ему алгоритм и детальные решения характерных примеров из-за довольно внушительного объема информации мы вынесли в отдельную статью - решение квадратных неравенств графическим способом.
Методом интервалов
Для решения квадратных неравенств с одной переменной помимо графического метода достаточно удобен метод интервалов, который сам по себе очень универсален, и подходит для решения различных неравенств, а не только квадратных. Его теоретическая сторона лежит за пределами курса алгебры 8, 9 классов, когда учатся решать квадратные неравенства. Поэтому здесь мы не будем вдаваться в теоретическое обоснование метода интервалов, а сосредоточимся на том, как с его помощью решаются именно квадратные неравенства.
Суть метода интервалов, по отношению к решению квадратных неравенств a·x2+b·x+c<0 (≤, >, ≥), состоит в определении знаков, которые имеют значения квадратного трехчлена a·x2+b·x+c на промежутках, на которые разбивается координатная ось нулями этого трехчлена (при их наличии). Промежутки со знаками минус составляют решения квадратного неравенства a·x2+b·x+c<0, со знаками плюс – неравенства a·x2+b·x+c>0, а при решении нестрогих неравенств к указанным промежуткам добавляются точки, отвечающие нулям трехчлена.
Познакомиться со всеми деталями этого метода, его алгоритмом, правилами расстановки знаков на промежутках и рассмотреть готовые решения типовых примеров с приведенными иллюстрациями Вы можете, обратившись к материалу статьи решение квадратных неравенств методом интервалов.
Путем выделения квадрата двучлена
Кроме графического метода и метода интервалов существуют и другие подходы, позволяющие решать квадратные неравенства. И мы подошли к одному из них, в основе которого лежит выделение квадрата двучлена в левой части квадратного неравенства.
Принцип этого способа решения квадратных неравенств состоит в выполнении равносильных преобразований неравенства, позволяющих перейти к решению равносильного неравенства вида (x−p)2<q (≤, >, ≥), где p и q – некоторые числа.
А как осуществляется переход к неравенству (x−p)2<q (≤, >, ≥) и как его решить разъясняет материал статьи решение квадратных неравенств путем выделения квадрата двучлена. Там же представлены примеры решения квадратных неравенств этим способом и даны необходимые графические иллюстрации.