Методические указания по освоению дисциплины
Б1.Б.8. Математика
| Вид образования: | Профессиональное образование |
| Уровень образования: | Высшее образование (бакалавриат) |
| Квалификация выпускника: | Бакалавр |
| Направление подготовки: | 38.03.06 «Торговое дело» 38.03.02 «Менеджмент» |
| Направленность (профиль) образовательной программы: | |
| Тип образовательной программы: | Программа бакалавриата |
| Форма обучения: | заочная |
| Срок освоения образовательной программы: | 4 года |
Нижневартовск - 2016 г.
Методические материалы, определяющие процедуры оценивания знаний, умений, навыков, характеризующих этапы формирования компетенций
Текущий контроль осуществляется в форме письменных контрольных работ, тестирования и проверки домашних заданий.
Промежуточный контроль освоения дисциплины осуществляется в рамках рейтинговой системы оценки. Экзаменационная оценка студента в рамках балльно-рейтинговой системы (БРС) является интегрированной оценкой выполнения студентом заданий во время практических занятий, выполнения домашних заданий, выполнения контрольных работ, сдачи коллоквиумов и результатов тестирования. Эта оценка характеризует уровень знаний, умений и навыков, приобретенных студентом в ходе изучения дисциплины.
По дисциплине приняты следующие критерии оценки:
Устные ответы:
- 1 балл выставляется студенту, если он излагает материал на уровне воспроизведения;
- 2 балла выставляется студенту, если он излагает материал на уровне понимания;
- 3 балла выставляется студенту, если он излагает материал на уровне применения
Решение задач:
- 1 балл выставляется студенту, если он знает формулы необходимые для расчета экономических показателей;
|
|
- 2 балла выставляется студенту, если он умеет сделать выбор моделей и формул для решения поставленной задачи;
- 3 балла выставляется студенту, если он анализирует и интерпретирует полученные результаты в соответствии с поставленной задачей.
Тесты:
Тест итогового контроля оценивается в 5 баллов (он состоит из теоретических вопросов и задач).
Доклады:
- 2 балла выставляется студенту, если он сумел подобрать необходимую литературу, но представляемая информация не систематизирована, не показал достаточно полного владения используемой терминологией;
- 4 балла выставляется студенту, если он сумел подобрать необходимую литературу, показал достаточно полное владение используемой терминологией, но представляемая информация не систематизирована.
- 6 баллов выставляется студенту, если он показал полное владение используемой терминологией, представляемая информация систематизирована, последовательна и логически связана, выводы обоснованы.
Контрольные работы:
– каждая оценивается в 3 балла (в соответствии с критериями оценки решения задач).
Максимальная сумма баллов, которую студент может набрать по дисциплине за семестр в ходе текущего контроля (за три контрольных недели) составляет 100 баллов, которые переводятся в традиционные оценки, согласно принятой в институте шкале перевода.
Студенты, набравшие по итогам работы в семестре менее 35 баллов, не допускаются к сдаче экзамена. Для получения допуска они должны добрать недостающее до 35 количество баллов, выполняя те текущие задания, которые они не выполнили в течение семестра.
|
|
Студенты, получившие по итогам работы в семестре не менее 61 балла, получают оценку за экзамен по дисциплине автоматически в соответствии со шкалой перевода баллов в оценки, принятой в НВГУ. Студенты, не получившие оценку за экзамен по дисциплине автоматически, или желающие улучшить полученную оценку, должны сдавать экзамен. В этом случае экзаменационная оценка студента выставляется в рамках традиционной четырехбалльной системы оценки на основе ответа студента на теоретические вопросы, а также правильности решения предложенных задач.
Методические указания к выполнению варианта 0 контрольной работы в 1 семестре
Задача 1. Разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:
X=άP+βQ+γR
Распишем это векторное уравнение покоординатно, т.е. сначала приравняем абсциссы, затем ординаты, а потом аппликаты. В результате получим систему трех линейных алгебраических уравнений с тремя неизвестными ά, β, γ:
1) Решим систему (1) методом Крамера. Для этого подсчитаем 4 определителя: главный ∆ и 3 вспомогательных ∆ά, ∆β, ∆γ. Напомним, что главный определитель составляется из коэффициентов при неизвестных ά, β, γ. Вспомогательные определители формируются из главного заменой соответствующего столбца столбцом свободных членов.
Главный определитель вычислим методом Лапласа с помощью разложения, например, по первой строке:
Аналогично вычисляются вспомогательные определители.
Неизвестные ά, β, γ находятся как отношения соответствующих вспомогательных определителей к главному:
|
|
2) Решим систему (1) матричным методом. Очевидно, что
X=A-1B,
где A-1 – обратная матрица по отношению к матрице коэффициентов системы, B – столбец свободных членов.
Найдем обратную матрицу по схеме:
A → A* → (A*)T → (A*)T/∆=A-1
где A – исходная матрица,
A* - присоединенная матрица (состоящая из алгебраических дополнений каждого элемента исходной матрицы),
(A*)T – транспонированная матрица относительно присоединенной матрицы A*,
∆ - определитель матрицы А
Напомним, что для нахождения присоединенной матрицы необходимо отыскать алгебраические дополнения всех элементов исходной матрицы. Алгебраическое дополнение элемента матрицы – это определитель, получающийся вычеркиванием строки и столбца, на пересечении которых находится данный элемент. Знак такого определителя меняется на противоположный, если сумма номеров строки и столбца нечетна.
Алгебраическим дополнением элемента (-1), находящегося на пересечении первой строки и первого столбца, является определитель
Алгебраическим дополнением элемента 0, находящегося на пересечении первой строки и второго столбца, является определитель
Знак определителя изменен на противоположный, так как 1+2=3 – нечетное число.
Аналогично отыскиваются алгебраические дополнения других элементов исходной матрицы.
Итак,
В результате транспонирования получаем
Определитель исходной матрицы был подсчитан ранее, а именно (см. формулу (2)), ∆=13. Таким образом,
Умножая справа на столбец свободных членов, находим
или ά=2, β=-3, γ=1.
Решим систему методом Гаусса. Составим расширенную матрицу
Пусть разрешающим элементом будет a23=1, а разрешающей строкой – вторая строка. С помощью выбранной второй строки элементарными преобразованиями исключим переменную γ, т.е. добьемся того, чтобы все элементы третьего столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить вторую, умноженную на (-3), то получим
Пусть теперь разрешающим элементом будет a32=1, а разрешающей строкой – третья строка. С помощью выбранной третьей строки элементарными преобразованиями исключим переменную β, т.е. добьемся того, чтобы все элементы второго столбца, кроме разрешающего, оказались равными 0. А именно, если к первой строке добавить третью, умноженную на (-6), а ко второй – третью, умноженную на 2, то получим
Сократим все элементы первого столбца на (-13):
Выберем в качестве разрешающего элемент a11=1. Прибавим ко второй строке первую, умноженную на (-4), а к третьей – первую, умноженную на (-2). После такого преобразования получаем
Отсюда снова получаем ά=2, β=-3, γ=1.
Итак, разложение вектора X=(1,7,1) по векторам P(-1,0,2), Q(0,-2,1,) R(3,1,0) имеет вид:
X=2P-3Q+R
Задача 2. Треугольник АВС задан своими вершинами
А(2,1), B(4,-3), C(-3,0).
1) Найдем уравнение стороны АВ, для чего воспользуемся уравнением прямой, проходящей через две точки:
Подставляя координаты точек А и В, получаем уравнение:
Итак, каноническое уравнение прямой АВ имеет вид:
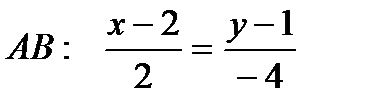
Приведем это уравнение к общему виду. По правилу пропорции получаем:
-4(x-2)=2(y-1). Раскрывая скобки, приходим к общему уравнению прямой АВ:
2x+y=5
Изолируем y и получим уравнение прямой с угловым коэффициентом:
y=-2x+5
Аналогично находятся уравнения других сторон. Каноническое уравнение прямой ВС:
Общее уравнение прямой ВС:
3x+7y+9=0
Уравнение прямой ВС с угловым коэффициентом:
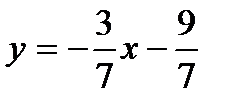
Каноническое уравнение прямой АС:
Общее уравнение прямой АС:
x-5y+3=0
Уравнение прямой АС с угловым коэффициентом:
2) Найдем уравнение и длину высоты AD из точки А на сторону ВС. Из канонического уравнения стороны ВС получаем направляющий вектор
qВС=(-7, 3)
Этот вектор можно принять в качестве нормального вектора прямой AD:
nAD=(-7, 3)
Следовательно, уравнение прямой AD, проходящей через точку А и имеющей нормальный вектор nAD, имеет вид:
-7(x-2)+3(y-1)=0
Раскроем скобки и приведем к общему виду:
-7x+3y+11=0
Уравнение медианы AD в явной форме имеет вид:
Далее найдем координаты точки D, для чего необходимо совместно решить уравнения прямой ВС и медианы AD:
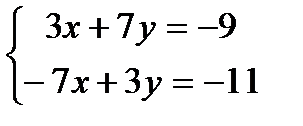
Решим эту систему методом Гаусса (алгебраического сложения). Умножим первое уравнение на 7, а второе на 3. После сложения этих уравнений переменная x исключается, что позволяет найти y. А именно,
y=-48/29
Теперь умножим первое уравнение на -3, а второе на 7. После сложения этих уравнений переменная y исключается, что позволяет найти x. А именно,
x=25/29
Проверим правильность решения системы линейных уравнений с помощью пакета символьных преобразований Maple:
> first:=-7*x+3*y=-11:
> second:=3*x+7*y=-9:
> sys:={first,second};
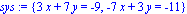
> solve(sys);
Итак, D(25/29, -48/29). Длину медианы AD находим по формуле расстояния между двумя точками:
3) Для вычисления площади треугольника найдем длину стороны ВС:
Тогда площадь треугольника ABC равна
Задача 3. Тетраэдр АВСD задан своими вершинами
А(2,1 4), B(-2,1,0), C(0,-3,-5), D(1,0,-3).
1) Найдем уравнение грани ABC через смешанное произведение векторов AB, AC и AM, где М(x,y,z) – произвольная точка грани:
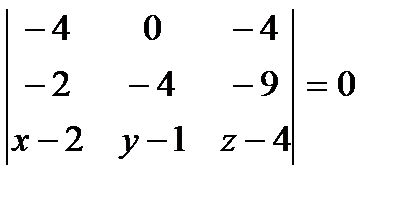
Разлагая определитель по третьей строке, получаем
-16(x-2)-28(y-1)+16(z-4)=0
или
ABC: 4x+7y-4z+1=0
Аналогично находятся уравнения других граней.
2) Уравнение средней линии грани АВС будем искать в следующей последовательности: сначала вычислим координаты точек P, Q – середин сторон АВ и АС. А именно, по формулам
находим: P(0,1,2). По аналогичным формулам Q(1,-1,-0.5). Уравнение средней линии PQ запишем в канонической форме:
или
3) Объем тетраэдра вычислим по формуле
где (AB,AC,AD) – смешанное произведение этих трех векторов. Итак,
Задача 4. Найти пределы функций:
1) Сначала подставим предельную точку x=2: числитель и знаменатель дроби равны нулю. Значит, мы имеем неопределенность первого типа 
. По теореме Виета или через дискриминант найдем корни квадратичной формы в числителе и разложим ее на линейные множители:
x2-x-2=(x-2)(x+1)
Теперь предел можно записать так:
2) Воспользуемся таблицей эквивалентных бесконечно малых, а именно,
sin2x~2x
(Это следствие из первого замечательного предела)
Тогда
Решим эту же задачу по правилу Лопиталя. Напомним, что по этому правилу отношение дифференцируемых бесконечно малых можно заменить отношением их производных. Тогда
3) Сделаем следующие преобразования:
Обозначим v=x/4 и снова воспользуемся таблицей эквивалентных бесконечно малых, а именно,
(Это второй замечательный предел).
Тогда
Задача 5. Исследовать функции и построить графики
Исследование функций проведем по следующей схеме:
А) общие характеристики
· область определения
· нули
· четность
· периодичность
· особые точки
· асимптоты
В) дифференциальные характеристики
· монотонность
· экстремумы
· выпуклость
· перегибы
1) Рассмотрим сначала функцию
· область определения – вся числовая прямая: D(y)=R
· нули – точки, в которых значение функции равно нулю. Очевидно, что один корень x1=2. Разделим (например, уголком) кубическую форму в правой части функции на линейный множитель (x-2) для отыскания еще двух других корней. Получим
x3-6x+4=(x-2)(x2+2x-2)
Квадратичная форма x2+2x-2 (по теореме Виета или через дискриминант) имеет два корня x2=-1-√3, x3=-1+√3. Таким образом,
D0={-1-√3, -1+√3, 2}
· Очевидно, что это функция общего вида, т.е. не обладает свойством четности
y(x) = y(-x)
или нечетности
y(x) = - y(-x)
· Функция не является периодической, т.е. не найдется такого Т, что
y(x)=y(x+Т)
· Особые точки: y(0)=4. Значит, график функции пересекает ось ординат в точке (0,4).
· Вертикальных асимптот нет, так как функция не имеет точек существенного разрыва (разрыва второго рода) хотя бы с одним односторонним бесконечным пределом. Убедимся, что нет и наклонных асимптот. Действительно, угловой коэффициент асимптоты равен
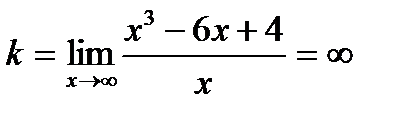
· Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода, т.е. точки, в которых производная равна нулю или не существует. Найдем производную
y’=3x2-6
и приравняем нулю:
x2-2=0.
Критические точки: - √2, √2. Они делят область определения на три участка монотонности:
D=(-∞, - √2)U( - √2, √2)U(√2, ∞)
Исследуем направление монотонности с помощью таблицы
| x | (-∞, - √2) | ( - √2, √2) | (√2, ∞) |
| y’ | + | - | + |
| y | ↑ | ↓ | ↑ |
Итак, участки монотонности:
(-∞, - √2) – участок возрастания функции
( - √2, √2) – участок убывания функции
(√2, ∞) - участок возрастания функции
· Из таблицы легко определить точки экстремума. А именно, x=-√2 – точка локального максимума функции, а x=√2 – точка локального минимума функции
· Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода, т.е. точки, в которых производная второго порядка равна нулю или не существует. Найдем производную второго порядка
y’’=6x
Приравнивая нулю, получаем одну точку x=0. Она делит область определения функции на два участка:
D=(-∞, 0)U(0, ∞)
Исследуем направление выпуклости с помощью таблицы
| x | (-∞, 0) | (0, ∞) |
| y’’ | - | + |
| y | ∩ | U |
Итак, участки выпуклости:
(-∞, 0) – участок выпуклости вверх
(0, ∞) - участок выпуклости вниз
· Из таблицы легко определить точку перегиба. А именно, x=0 – точка перегиба функции
Используя полученную информацию, построим график заданной функции с помощью пакета Maple.
plot(x^3-6*x+4,x=-3..3);
2) Рассмотрим теперь функцию 
· область определения – все точки числовой прямой, за исключением точки x=0: D(y)=R\{0}
· нули – точки, в которых значение функции равно нулю.Приравнивая нулю числитель, получаем
D0={-2, 2}
· Очевидно, что это нечетная функция. В самом деле,
Значит, график функции симметричен относительно начала координат.
· Функция также не является периодической, т.е. не найдется такого Т, что
y(x)=y(x+Т)
· Особые точки: x=0. Найдем односторонние пределы в этой точке:
· Полученные значения односторонних пределов позволяются сделать вывод, что функция имеет вертикальную асимптоту x=0. Убедимся, что функция имеет и наклонную асимптоту y=kx+b. Действительно,
Следовательно, y=-x+b. Найдем параметр b.
Итак, наклонная асимптота заданной функции такова: y=-x
· Исследуем функцию на монотонность. Для этого вычислим критические точки первого рода. Найдем производную
Проверим правильность дифференцирования в среде Maple:
> diff((4-x^2)/x,x);
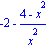
Критическая точка: 0. Она не входит в область определения функции, но является граничной для нее. Область определения в этом случае естественным образом представляется объединением двух участков монотонности:
D=(-∞,0)U(0, ∞)
Исследуем направление монотонности с помощью таблицы
| x | (-∞, 0) | (0, ∞) |
| y’ | - | - |
| y | ↓ | ↓ |
Итак, участки монотонности:
(-∞, 0) – участок убывания функции
(0, ∞) - участок убывания функции
· Из таблицы видно, что экстремумов функция не имеет
· Исследуем функцию на выпуклость. Для этого вычислим критические точки второго рода. Найдем производную второго порядка
Проверим правильность дифференцирования в среде Maple:
> diff(-(x^2+4)/(x^2),x);
Критическая точка: x=0. Она делит область определения функции на те же два участка:
D= (-∞, 0) U (0, ∞)
Исследуем направление выпуклости с помощью таблицы
| x | (-∞, 0) | (0, ∞) |
| y’’ | - | + |
| y | ∩ | U |
Итак, участки выпуклости:
(-∞, 0) – участок выпуклости вверх
(0, ∞) - участок выпуклости вниз
· Точка x=0 не является точкой перегиба, так как она не входит в область определения функции и в ней не существует производная второго порядка.
Используя полученную информацию, построим график заданной функции
Методические указания к выполнению варианта 0 контрольной работы во 2 семестре
Задача 1. Найти интегралы:
1) Выделим в числителе производную от знаменателя:
Такое разложение позволяет использовать известные табличные интегралы
Тогда
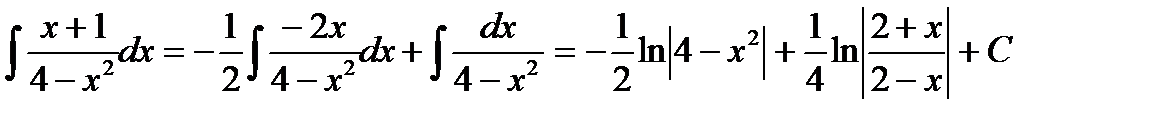
Итак,
Проверим результат с помощью Maple:
Ø int((x+1)/(4-x^2),x);
Очевидно, что результаты ручного и машинного вычислений совпадают.
2) Такой интеграл будем брать методом интегрирования по частям, а именно, по формуле
Пусть u=x, dv=cos3xdx. Тогда du=dx, v=(1/3)sin3x. Далее получаем
Проверим результат также с помощью Maple:
Ø int(x*cos(3*x),x);
3) Подинтегральная функция представляет собой правильную рациональную дробь. Разложим ее на простейшие дроби с неопределенными коэффициентами. Для этого в знаменателе выделим линейные или неприводимые квадратичные множители:
Из этого равенства получаем
x-2=A(x+3)+Bx
Раскроем скобки и приравняем коэффициенты при одинаковых степенях х.
x-2=Ax+3A+Bx или x-2=(A+B)x+3A
Отсюда получаем систему линейных алгебраических уравнений:
Решая эту систему, находим A=-(2/3), B=5/3.
Подставим полученные значения (бывших) неопределенных коэффициентов Имеем
Переходя к интегралам, получаем
Итак,
Снова проверим результат с помощью Maple:
Ø int((x-2)/(x^2+3*x),x);
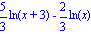
Задача 2. Вычислить площадь, ограниченную линиями:
Представим на графике указанную площадь. Для этого вычертим параболу 
и прямую 
, а затем выделим фигуру, заключенную между этими геометрическими объектами. Вычисление площади этой фигуры с помощью определенного интеграла потребует знания пределов интегрирования. Это нижняя и верхняя границы проекции фигуры на ось абсцисс. Для нахождения таких границ приравняем правые части заданных уравнений: x2-x+3=7-x. Отсюда x2-4=0. Значит, x1=-2, x2=2.
Площадь выделенного участка вычислим с помощью определенного интеграла:
Проверка в среде Maple:
Ø int(4-x^2,x=-2..2);
Задача 3. Отыскать условный экстремум функции
z=x2+3xy-y+2→extr, x+y=5
Составим функцию Лагранжа (для сведения условной задачи к безусловной):
L(x,y,λ)= x2+3xy-y+2+ λ (5-x-y)
Сначала найдем частные производные этой функции:
L’x(x,y,λ)= 2x+3y-λ
L’y(x,y,λ)= 3x-1-λ
L’λ(x,y,λ)= 5-x-y
Затем приравняем их к нулю. Получаем, вообще говоря, нелинейную систему уравнений относительно неизвестных x и y:
2x+3y-λ=0
3x-1-λ=0
5-x-y=0
Исключим параметр λ из первых двух уравнений. Получаем систему двух уравнений:
x-3y=1
x+y=5
Отсюда x=4, y=1.
Итак, точка P(4,1) – критическая (подозрительная на экстремум).
С помощью пакета Maple изобразим поверхность, соответствующую заданной функции двух переменных:
plot3d(x^2+3*x*y-y+2,x=-5..5,y=-5..5);
Из рисунка видно, что геометрическим образом заданной функции является гиперболический параболоид (седло). При пересечении с плоскостью x+y=5 образуется парабола (ветви вниз). Действительно, подставляя y=5-x в правую часть заданной функции, получаем z=-2x2+16x-3. Это проекция пространственной параболы на координатную плоскость Oxz. Подставляя x=5-y в правую часть заданной функции, получаем z=-2y2+4y+27. Это проекция пространственной параболы на координатную плоскость Oyz. Таким образом, P(4,1) – точка условного максимума.
Замечание. Более точное исследование критической точки в данной задаче можно провести, используя теорию квадратичных форм.
Задача 4. Решить задачу Коши для линейного дифференциального уравнения первого порядка:
Данное уравнение можно решить методом Лагранжа, представив искомое решение в виде произведения двух функций: y=uv. Дифференцируя и подставляя в уравнение, получаем:
Объединим второе и третье слагаемые и вынесем за скобку общий множитель u. Имеем:
Решаем теперь два вспомогательных уравнения:
Найдем интеграл отдельно методом интегрирования по частям:
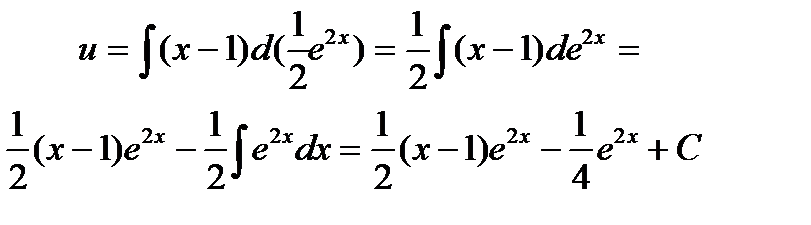
Итак, общее решение данного линейного уравнения таково:
Для нахождения частного решения подставим начальные условия в общее решение. А именно, вместо х подставим 0, а вместо y - число 1. Получаем
Таким образом, частное решение данной задачи таково:
Приведем решение этого дифференциального уравнения в среде Maple:
> L:=diff(x(t),t$1)+2*x(t)=t-1;
> dsolve({L,x(0)=1},x(t));
Задача 5. Решить задачу Коши для линейного неоднородного дифференциального уравнения второго порядка:
Из теории обыкновенных дифференциальных уравнений известно, что общее решение такого уравнения y складывается из общего решения соответствующего однородного y0 и частного решения неоднородного уравнения z:
y=y0+z
Для нахождения общего решения однородного уравнения составим характеристическое уравнение:
r2-9r+18=0
Его корни: 3, 6. Если корни характеристического уравнения действительны и различны, то общее решение однородного уравнения имеет вид:
y=C1e3x+C2e6x
Найдем частное решение неоднородного уравнения. Правая часть y=2x имеет специальный вид, а именно, является многочленом первой степени. Значит, частное решение можно искать в виде y=ax+b, где a и b – неопределенные коэффициенты. Далее находим производные: y’=a, y’’=0. Подставим в исходное уравнение: 0-9a+18(ax+b)=2x. Раскроем скобки и приравняем коэффициенты при одинаковых степенях х:
Отсюда a=1/9, b=1/18. Таким образом, частное решение неоднородного уравнения
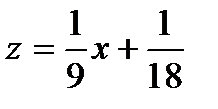
Тогда общее решение исходного уравнения
Для решения задачи Коши необходимо найти производную общего решения:
Используя начальные условия, получаем
Полученную систему перепишем так:
Решая ее относительно неизвестных С1 и С2, получаем С1=-11/27, С2=19/54. Ответ:
Приведем решение этого дифференциального уравнения в среде Maple:
> L:=diff(x(t),t$2)-9*diff(x(t),t$1)+18*x(t)=2*t;
> dsolve({L,x(0)=0,D(x)(0)=1},x(t));
Задача 6. Указать область сходимости степенного ряда
В соответствии с признаком Даламбера положительный ряд сходится, если
где 
. Таким образом,
Решая это неравенство, находим
Исследуем сходимость данного степенного ряда в граничных точках. При x=1 данный ряд превращается в числовой сходящийся ряд:
Это известный условно сходящийся ряд Лейбница.
При x=5 данный ряд расходится:
Итак, область сходимости заданного степенного ряда – полуинтервал: [ 1,5).
Составитель приложения 2: Дмитриев Николай Пименович, доцент кафедры ФМО