Б КЛАСС УРОК 14.04.2020
Тема. Бесконечные периодические десятичные дроби. 
Цель. Дать определение периодической десятичной дроби. Научиться представлять обыкновенную дробь в виде периодической дроби.
Ход урока.
Читаем теорию, пример 1 и 2 разбираем устно.
Объяснение нового материала.
Итак, мы знаем, что если знаменатель несократимой дроби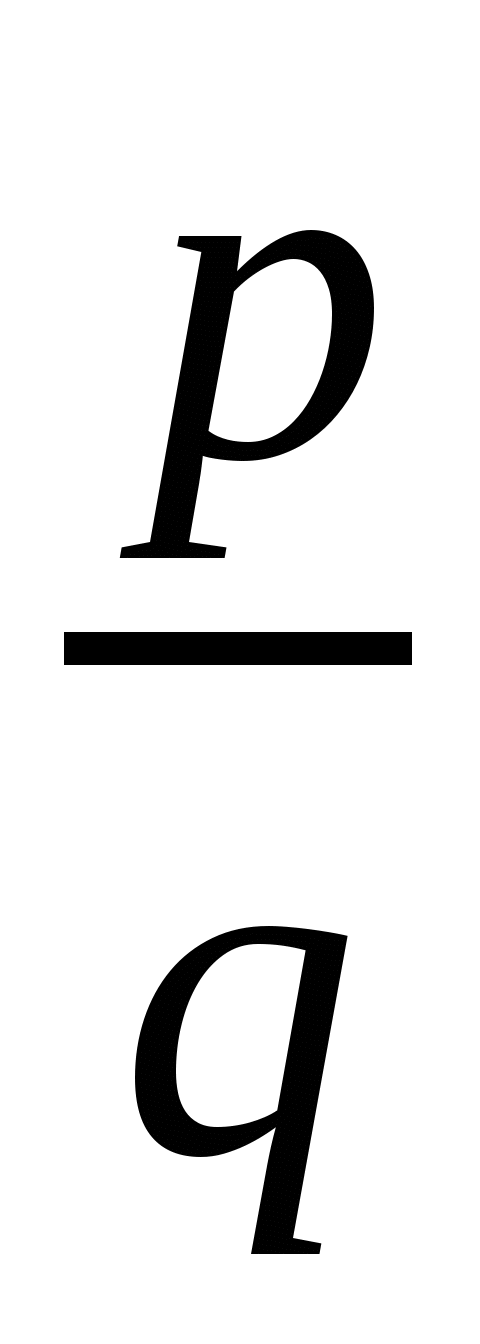 
имеет простой делитель, отличный от 2 и 5, то эта дробь не разлагается в конечную десятичную дробь. Поэтому при делении числителя этой дроби на знаменатель уголком не может получится конечная десятичная дробь.
Определение. Бесконечные десятичные дроби, в которых одна или несколько цифр неизменно повторяются в одной и той же последовательности, называются периодическими десятичными дробями. Совокупность повторяющихся цифр называется периодом этой дроби(это определение выписать в тетрадь)
Пример 1.
1)Разложите в десятичную дробь число: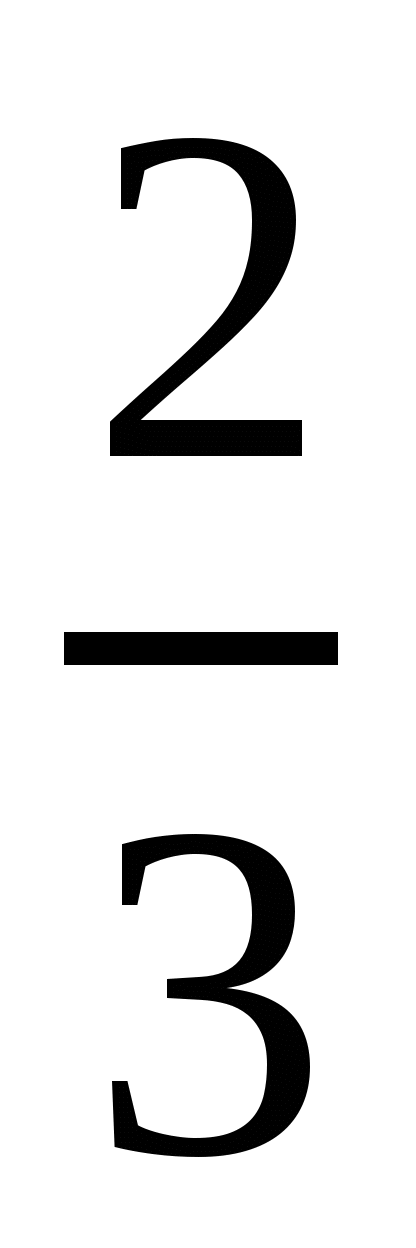 
.
1. Сократима ли дробь?
2 
. Смотрим на знаменатель несократимой дроби, он имеет простой делитель 3, отличный от 2 и 5, то эта дробь заведомо не разлагается в конечную десятичную дробь.
3. Разделим числитель на знаменатель уголком.
4. На каждом этапе вычисления получается один и тот же остаток 2. Процесс этот бесконечен. Он приводит к выражению 0,666..., где точки означают, что цифра 6 повторяется бесконечно много раз.
.
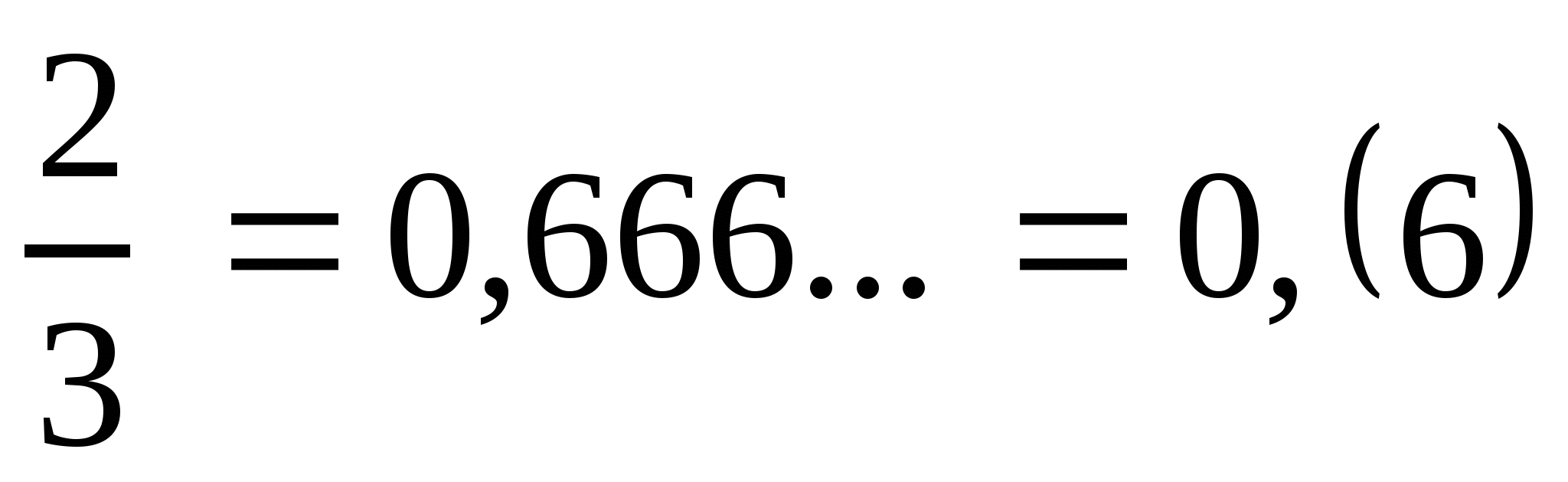Читают: «нуль целых и шесть в периоде». Цифру 6 называют периодом дроби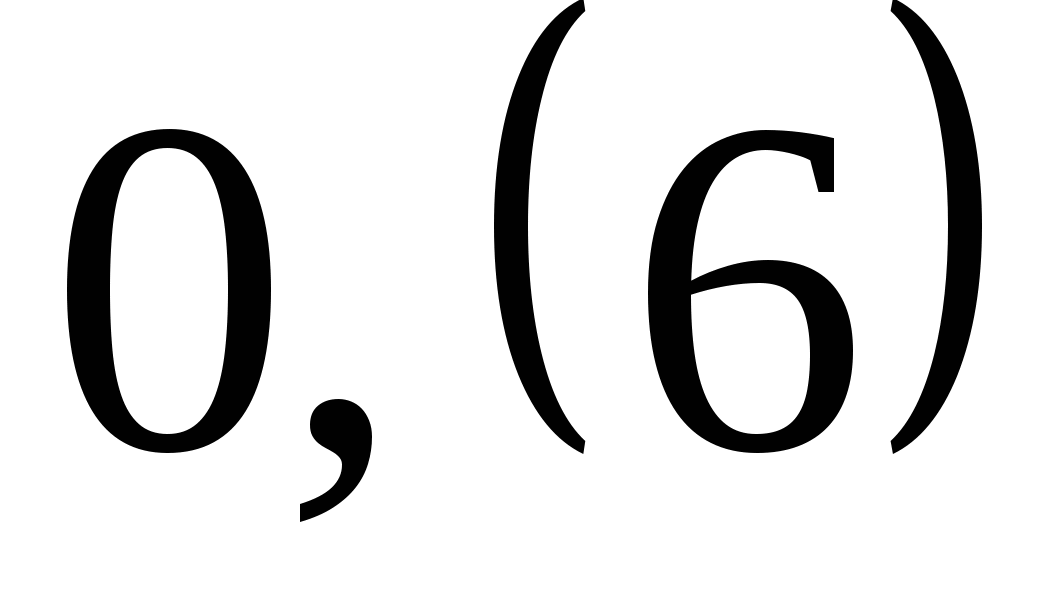 
.
Говорят, что число 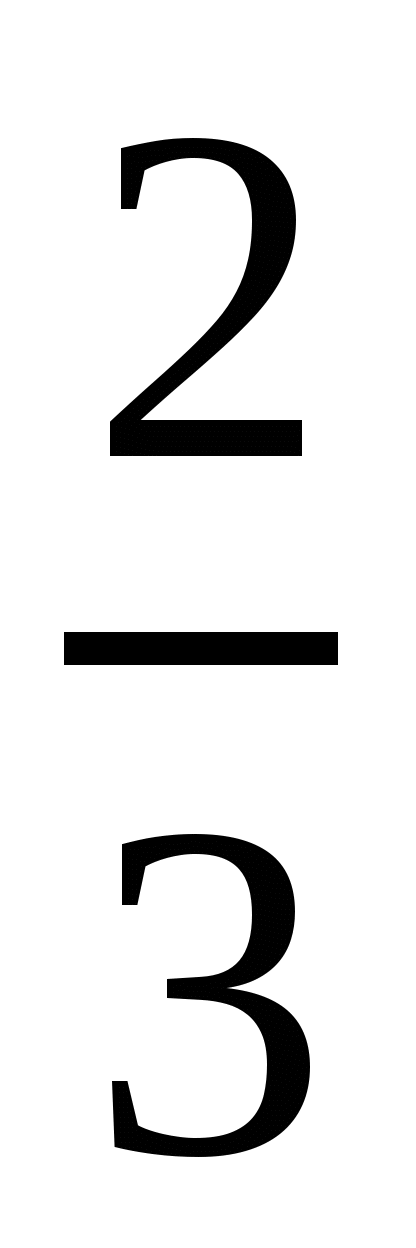представлено в виде периодической дроби .
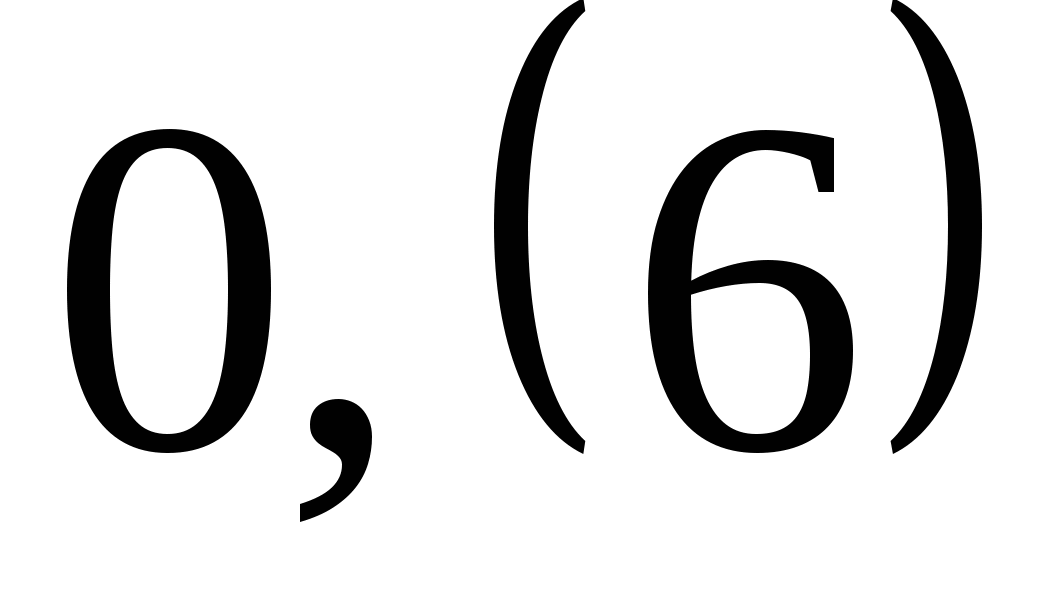2) Разложи 
те в десятичную дробь число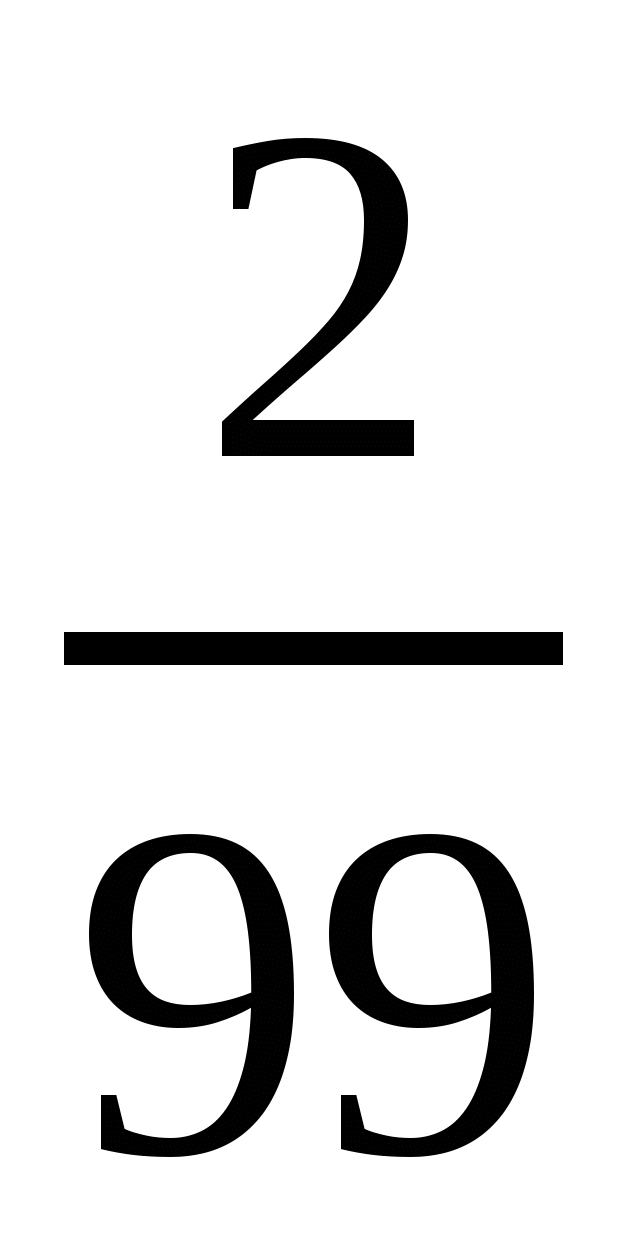 
.
1. Сократима ли дробь?
2. Смотрим на знаменатель несократимой дроби, он имеет простой делитель 3 и 11, отличный от 2 и 5, то эта дробь заведомо не разлагается в конечную десятичную дробь.
|
|
3. Разделим числитель на знаменатель уголком.
4. На каждом этапе вычисления получается один и тот же остаток 20. Процесс этот бесконечен. Он приводит к выражению 0,0202..., где точки означают, что цифры 0 2 повторяются бесконечно много раз.
.
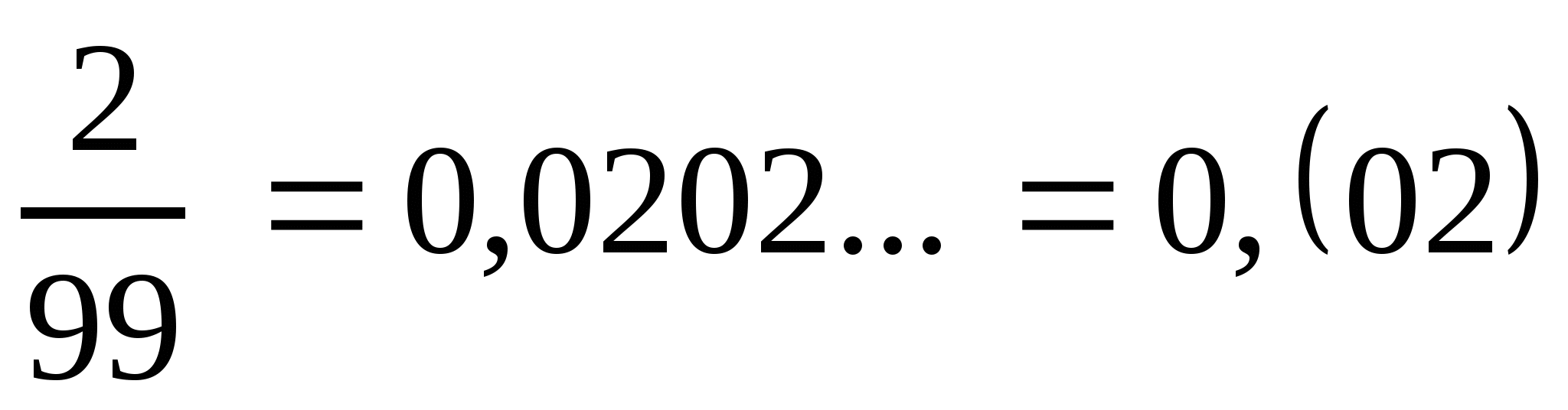Читают: «нуль целых и нуль два в периоде». Цифры 0 2 называют периодом дроби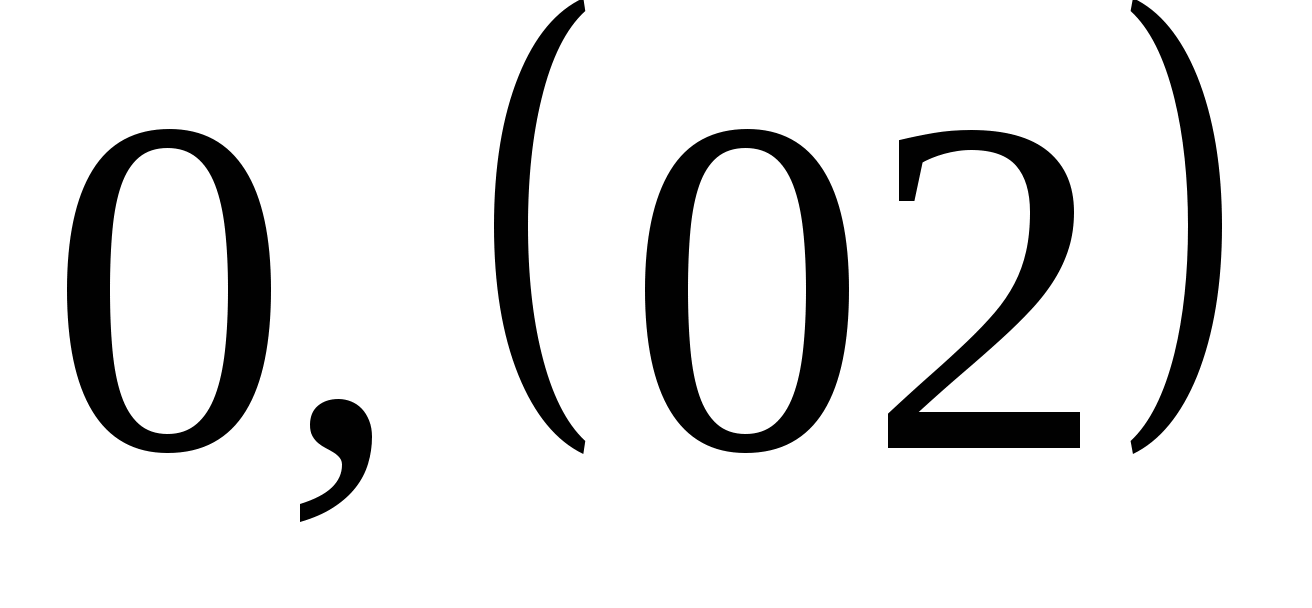 
.
Говорят, что число 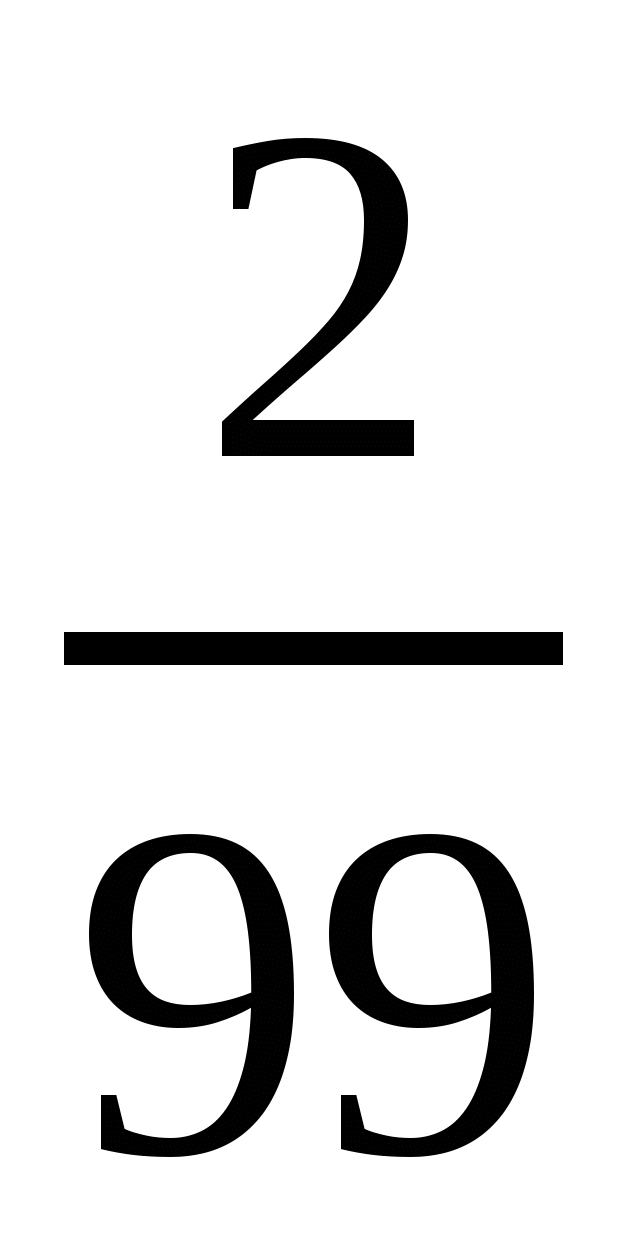представлено в виде периодической дроби .
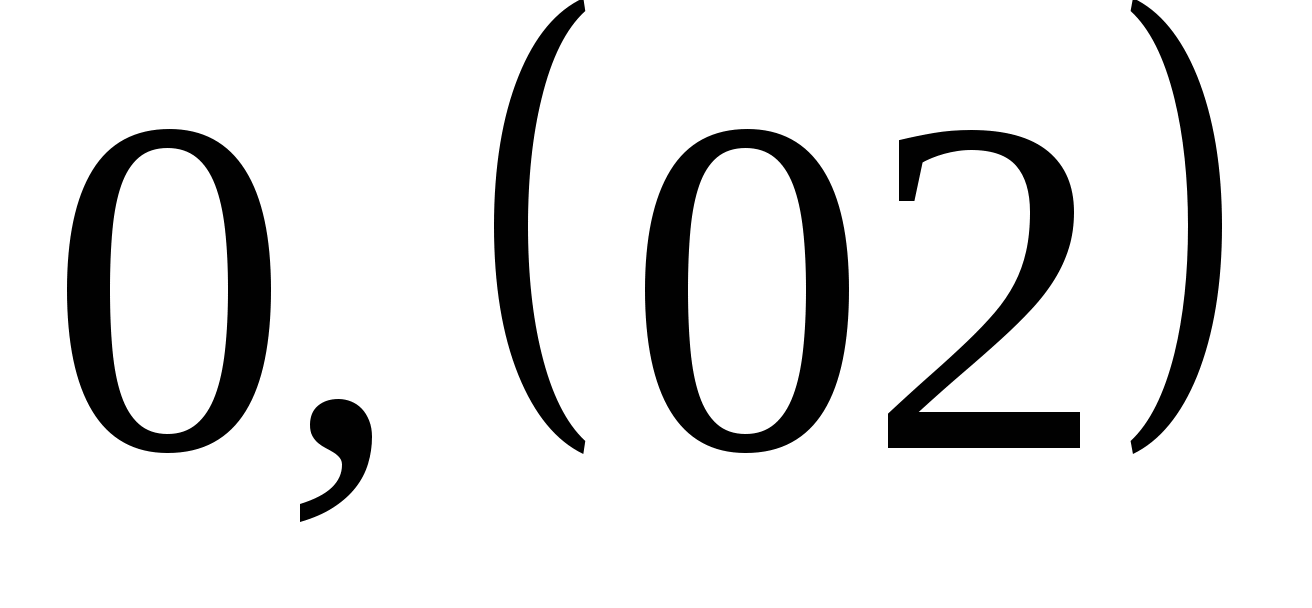3) Разложите в десятичную дробь число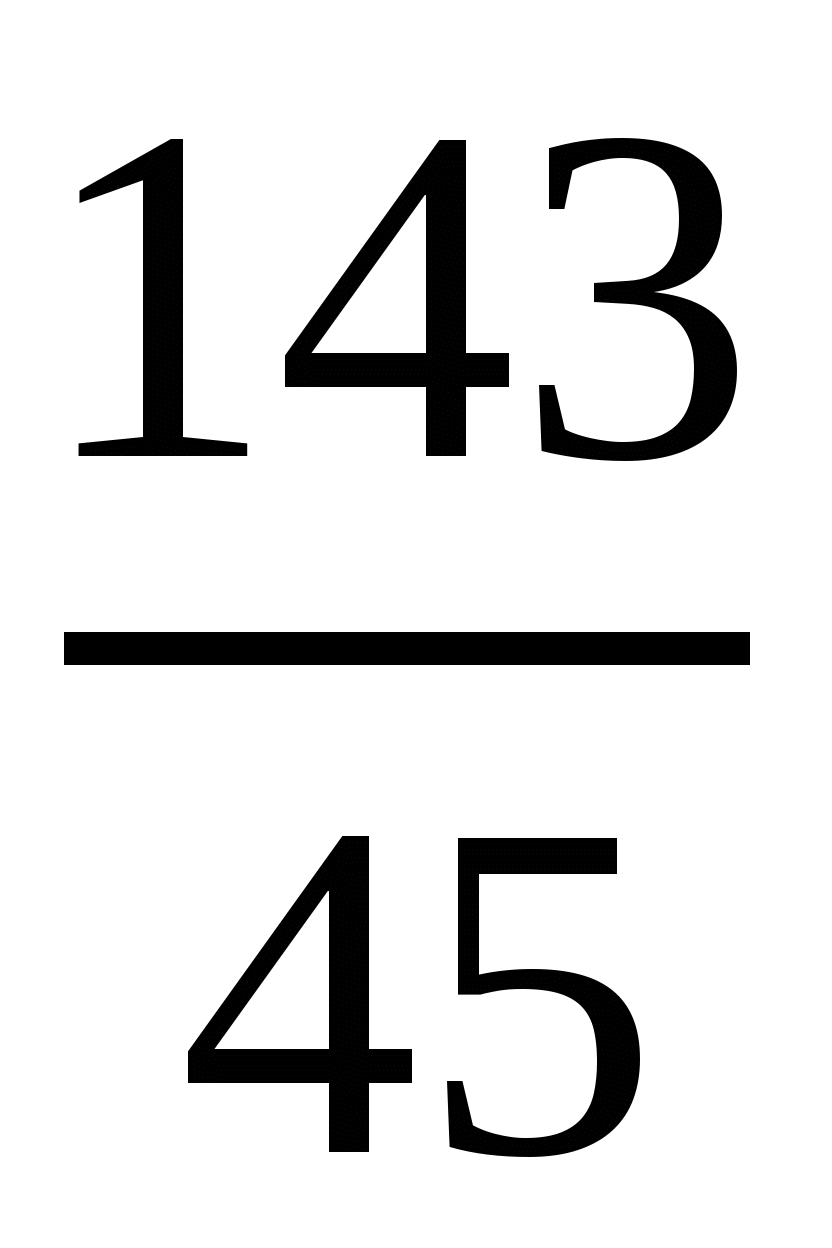 
.
1 
. Сократима ли дробь?
2. Смотрим на знаменатель несократимой дроби, он имеет простой делитель 3, отличный от 2 и 5, то эта дробь заведомо не разлагается в конечную десятичную дробь.
3. Разделим числитель на знаменатель уголком.
4. На каждом этапе вычисления получается один и тот же остаток 35. Процесс этот бесконечен. Он приводит к выражению 3,177..., где точки означают, что цифра 7 повторяется бесконечно много раз.
.
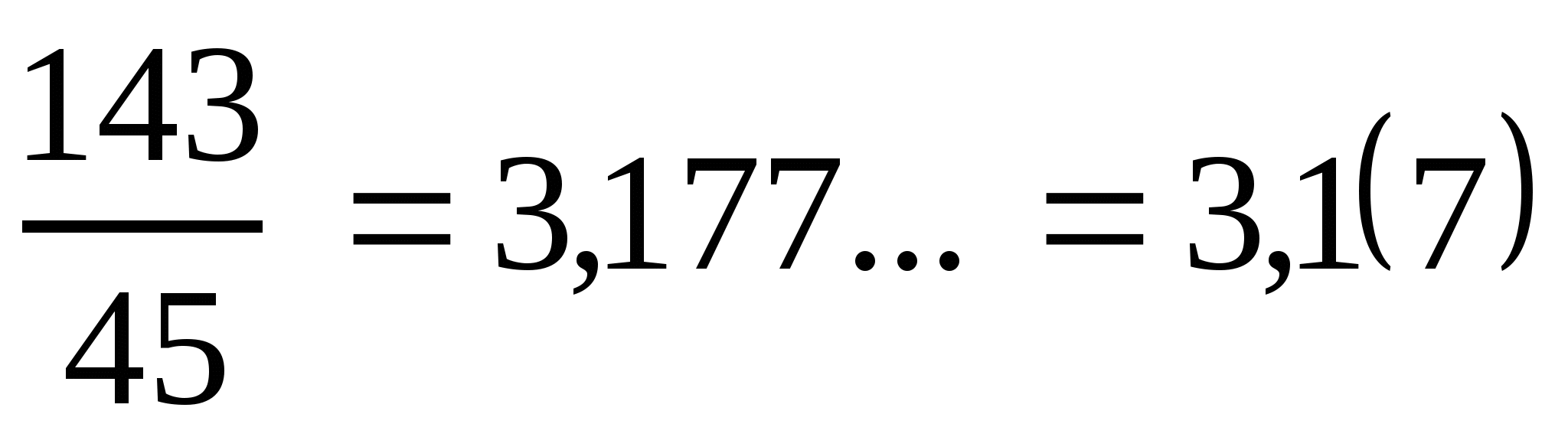Читают: «три целых, одна десятая, и семь в периоде». Цифра 7 называет периодом дроби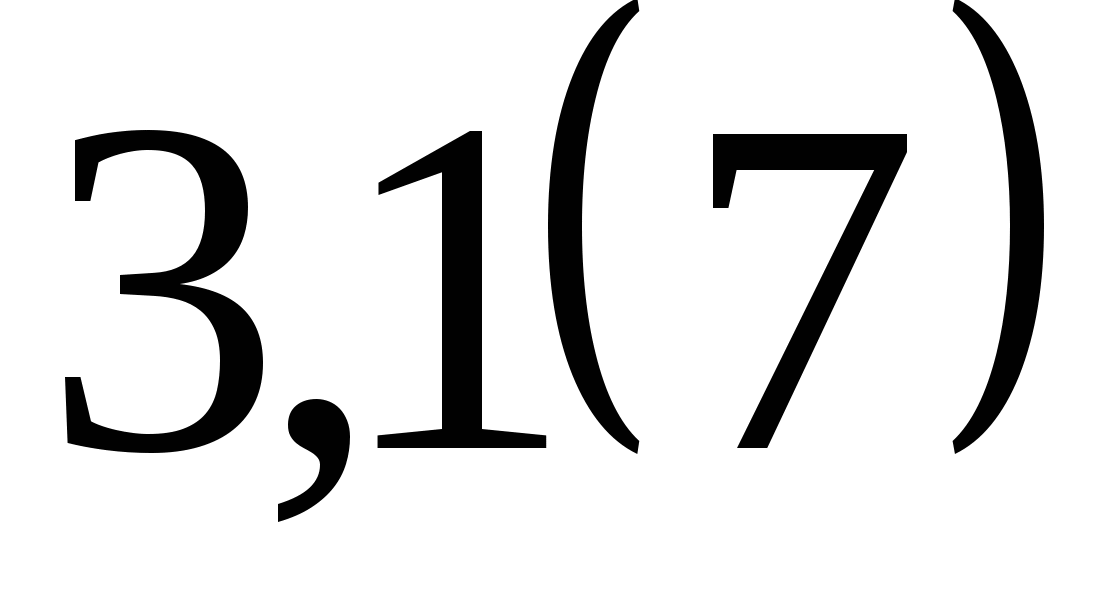 
.
Говорят, что число 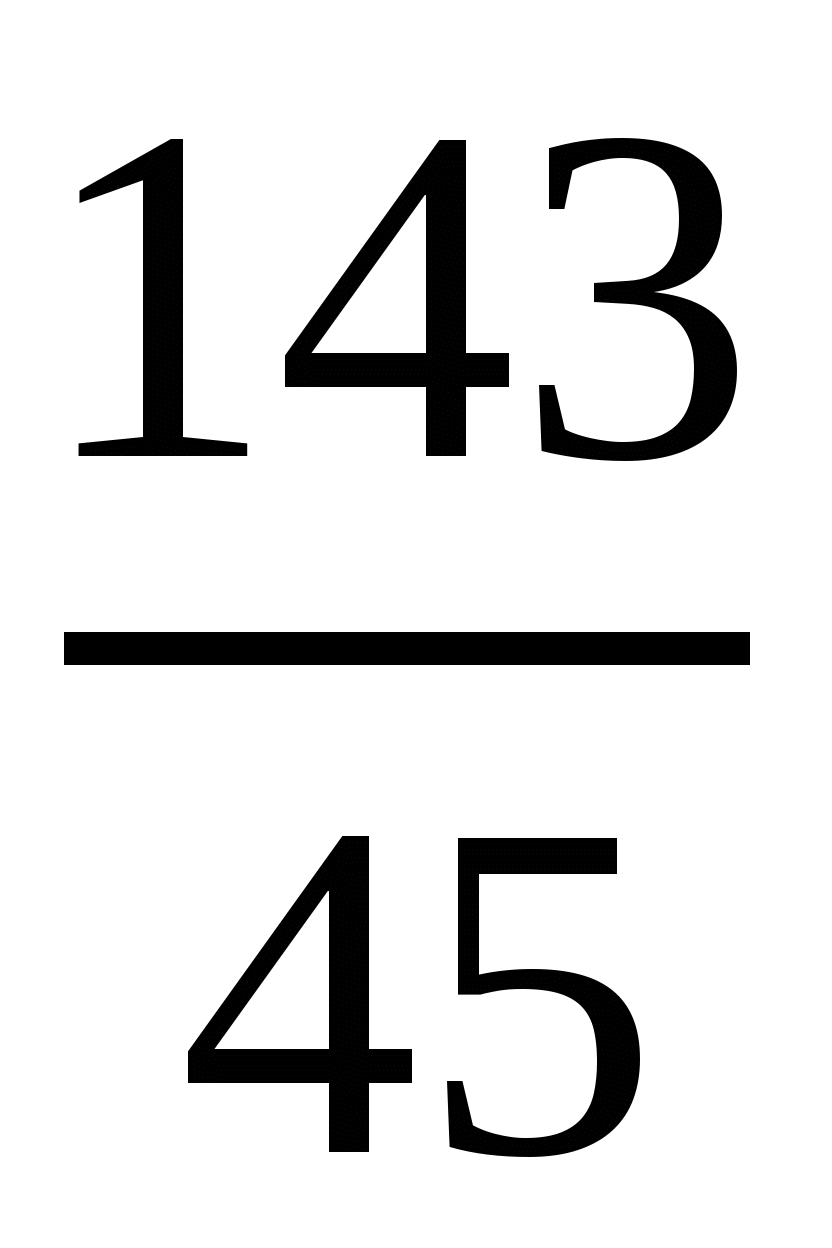представлено в виде периодической дроби .
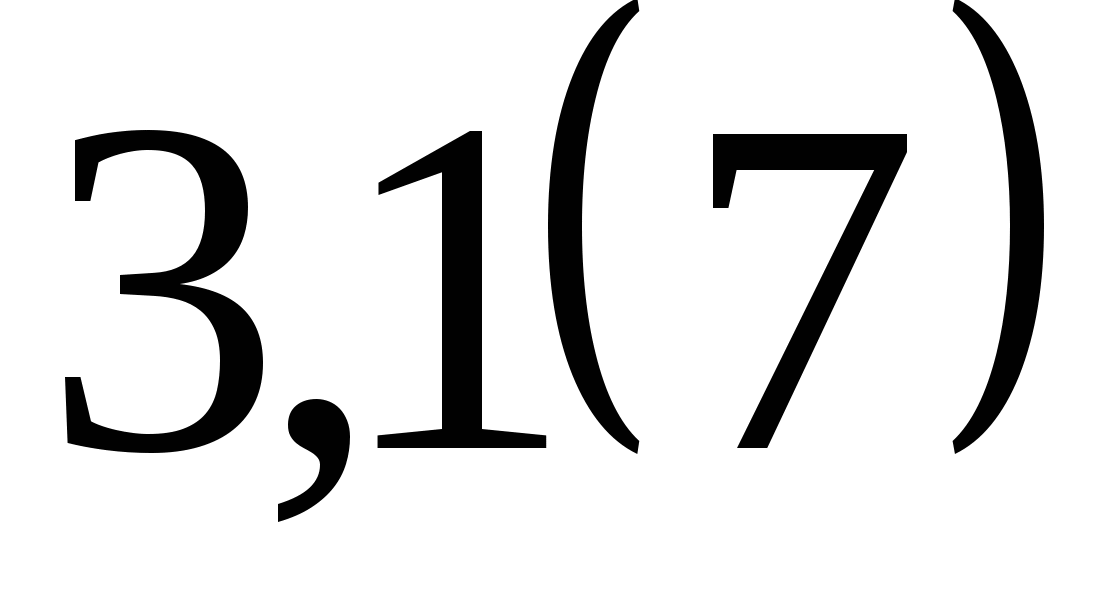Вообще, если числитель положительной несократимой дроби разделить на её знаменатель уголком, то в частном получится, либо конечное, либо бесконечное периодическое её десятичное разложение.
Поставим перед положительной дробью знак «– », получим отрицательную периодическую дробь.
Пример 2. Разложите в десятичную дробь число:
1) 
;
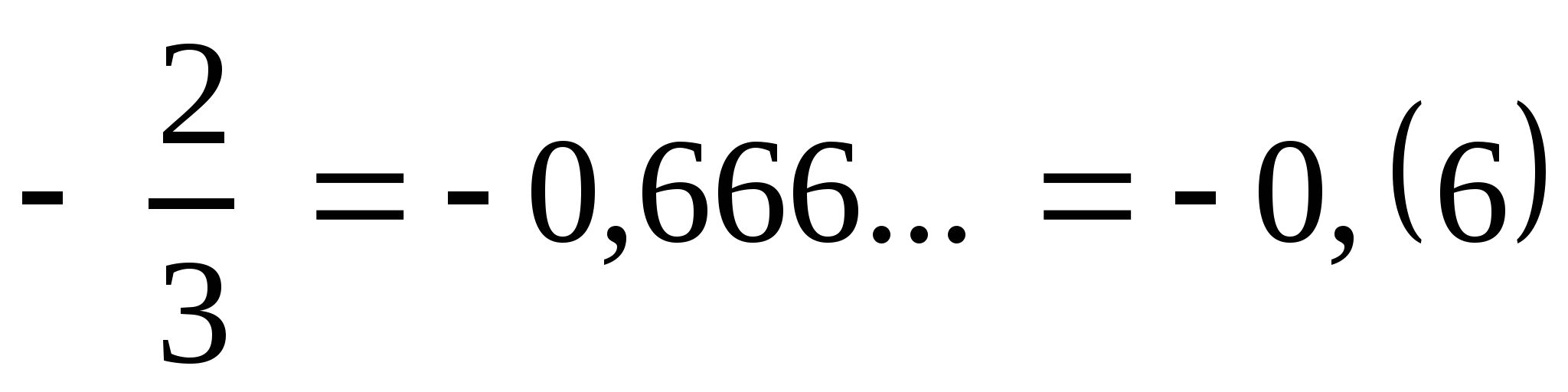2) 
;
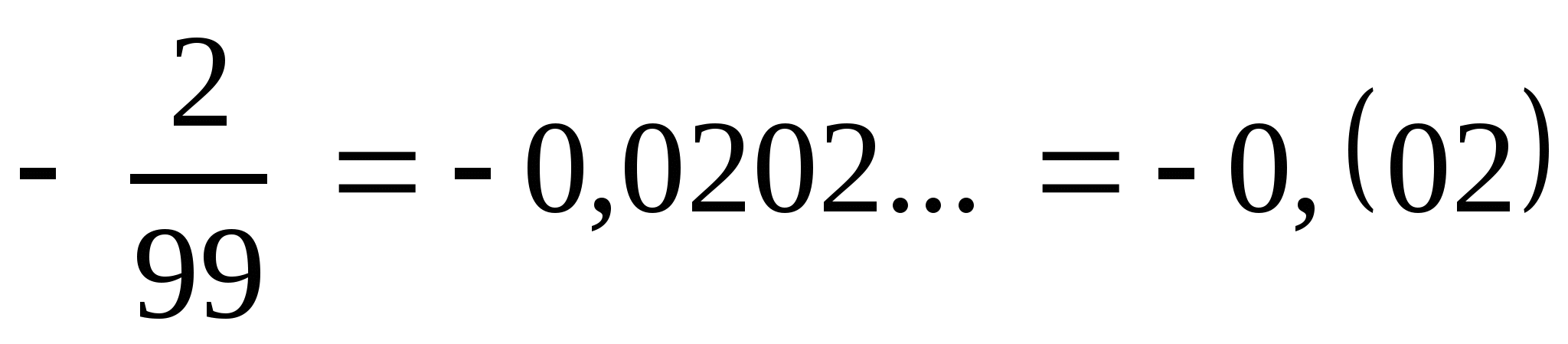3) 
.
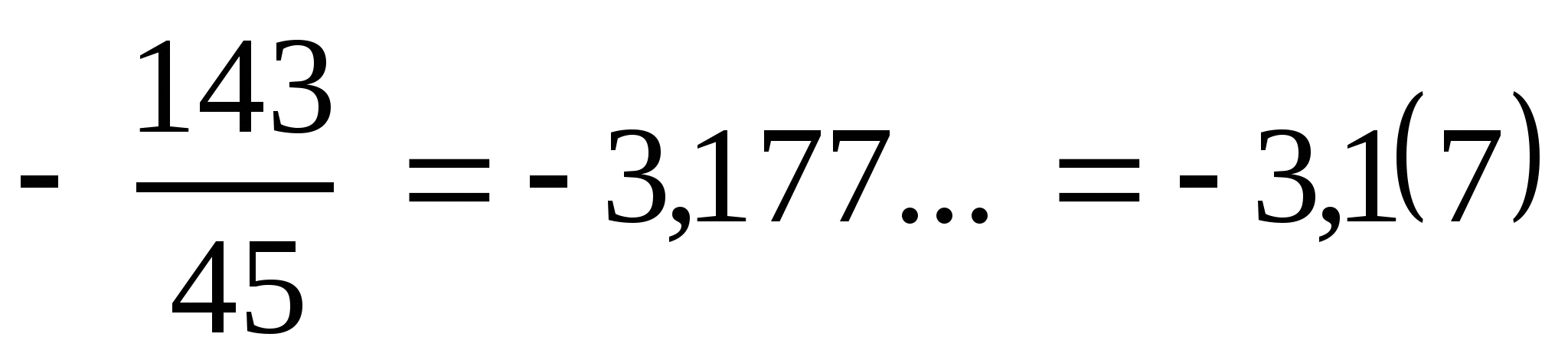Приписывая к целому числу (после запятой) или к конечной десятичной дроби бесконечно много нулей, мы превращаем её в равную ей бесконечную периодическую десятичную дробь с периодом 0.
|
|
Пример 2. Разложите в десятичную дробь число:
1) 
;
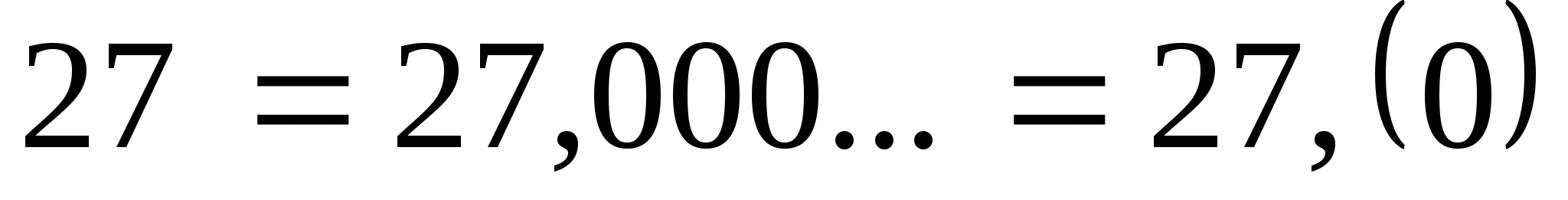2) 
;
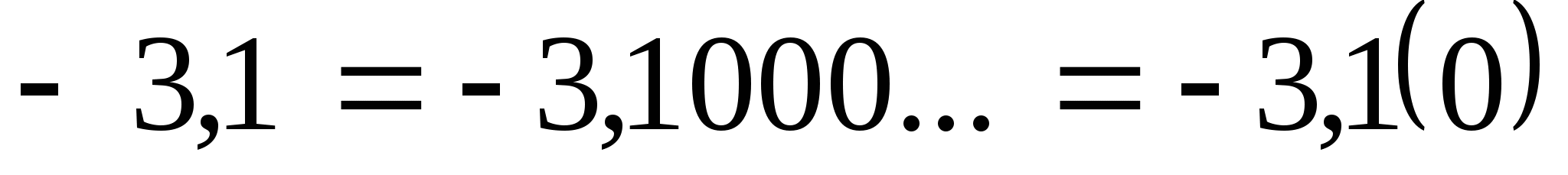3) 
.
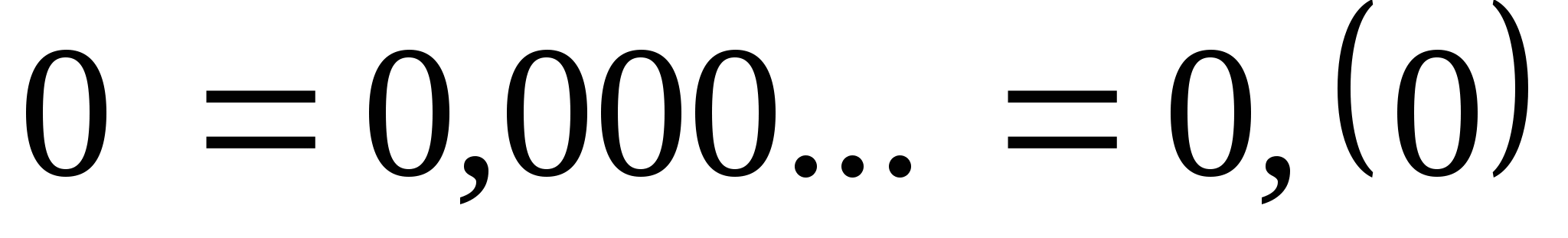Следовательно, любое целое число и любую конечную десятичную дробь можно считать периодической дробью с периодом 0.
Итак, любое рациональное число 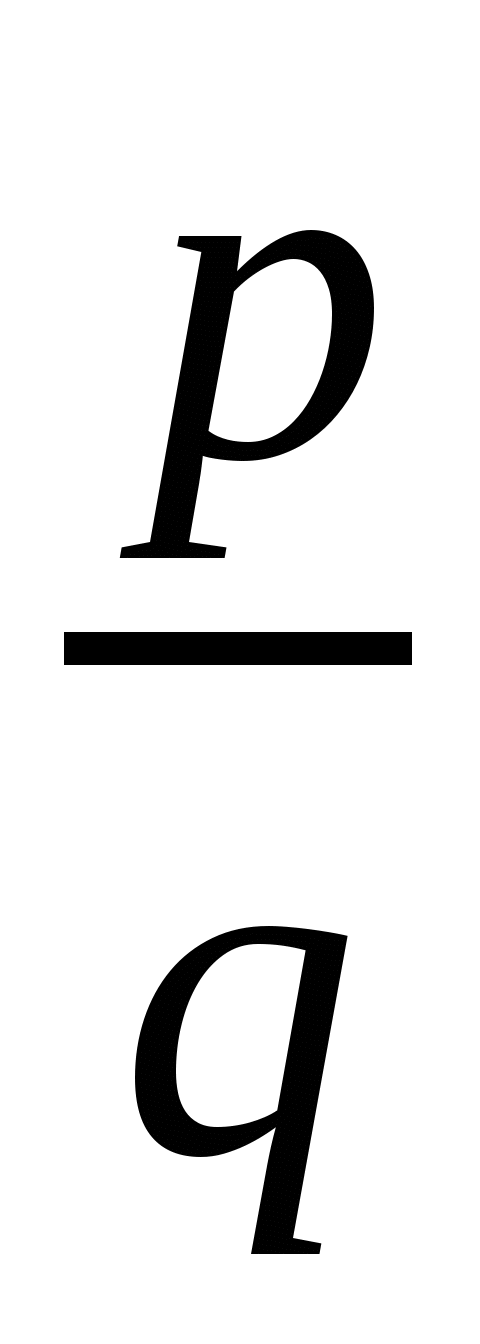разлагается в периодическую дробь.
V. Решение упражнений(далее записываем в тетрадь)
Уч.с.194 № 973(1ст.). Запишите число в виде периодической дроби, назовите ее период:
а)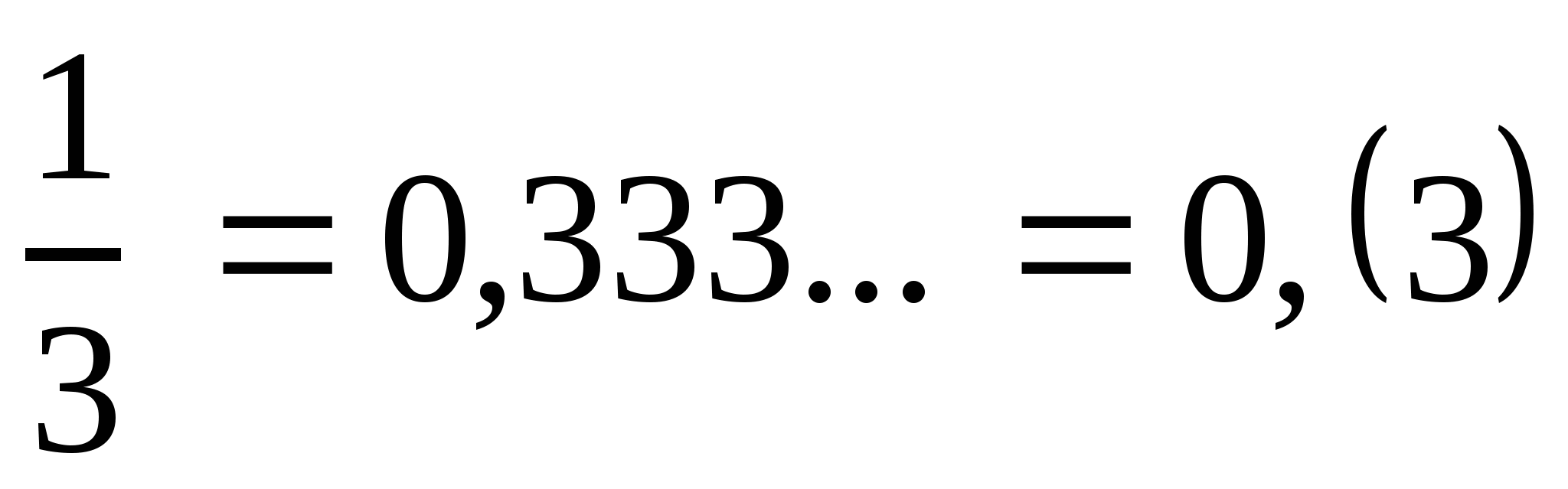 
;
е)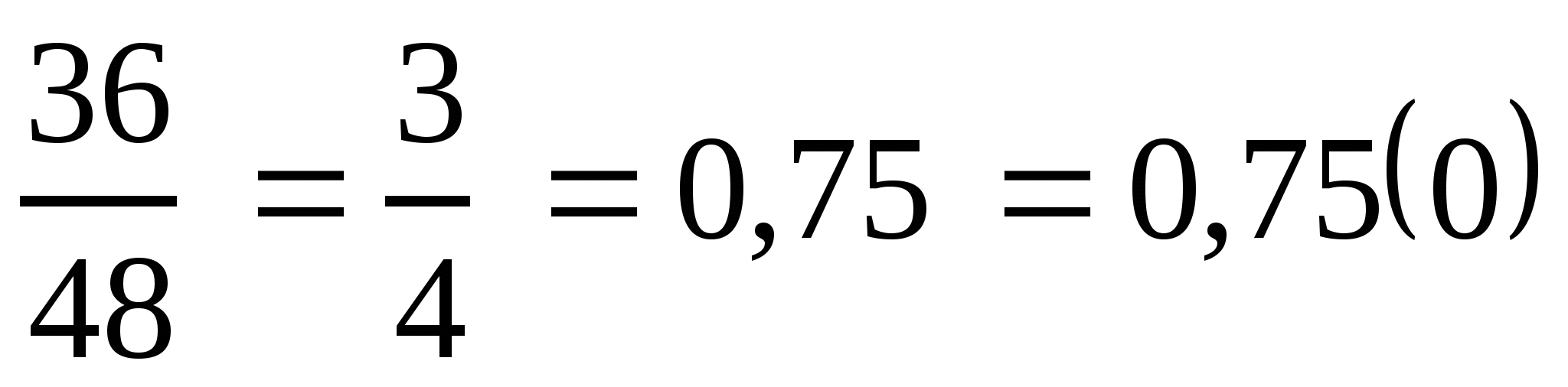 
;
л)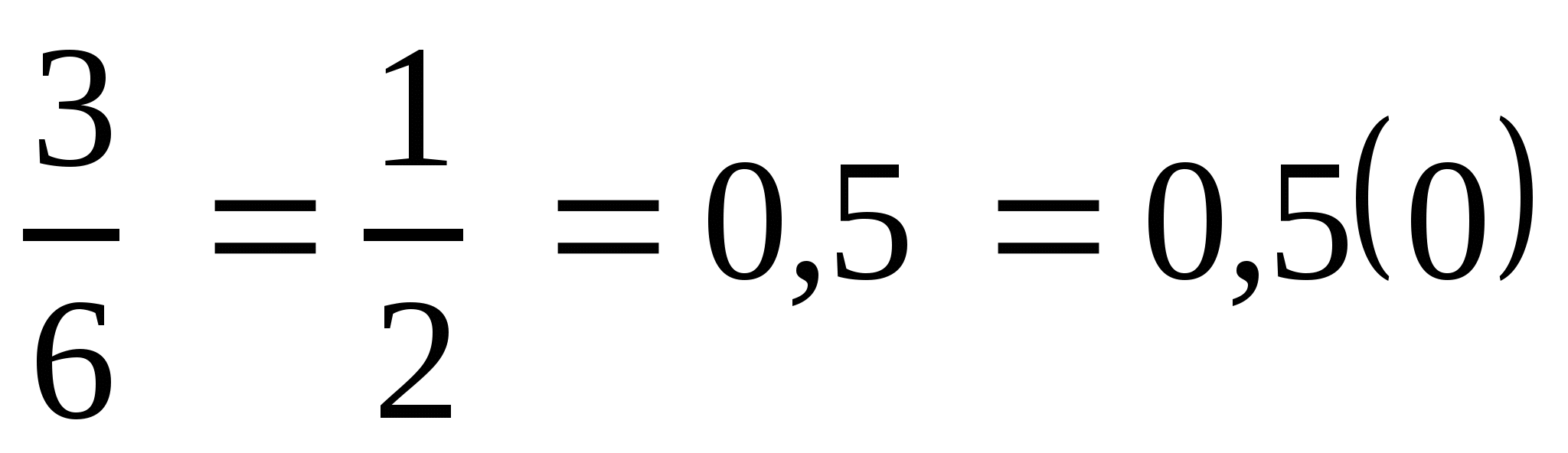 
.
Уч.с.194 № 974(а). Разложите обыкновенную дробь в периодическую делением числителя на знаменатель уголком:
а)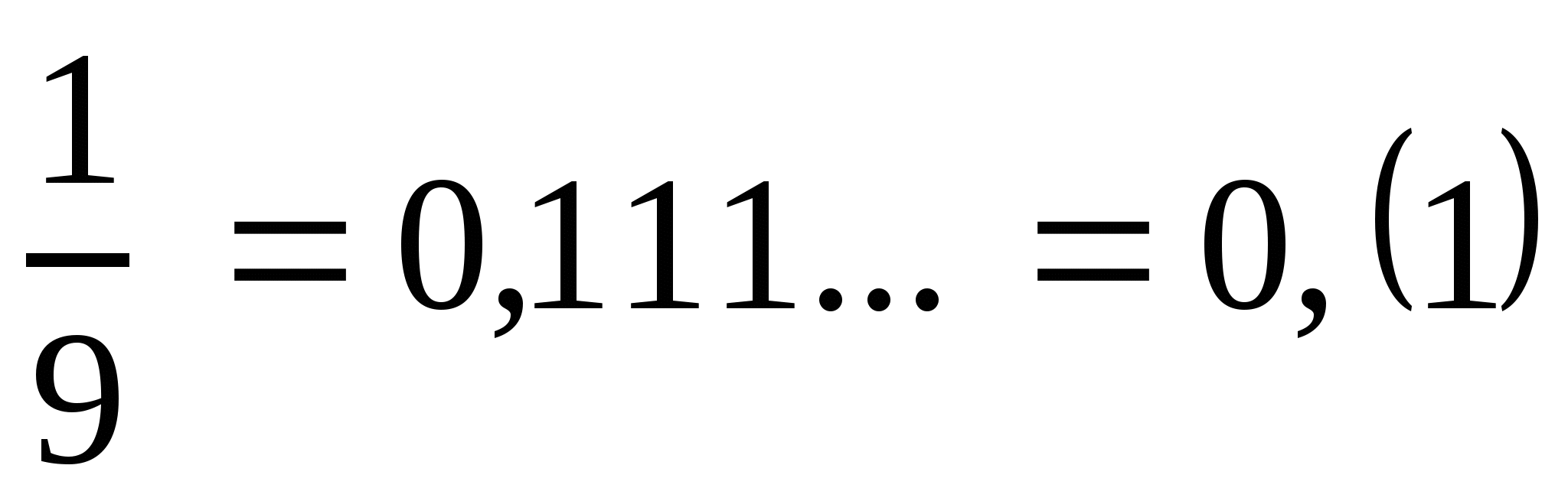 
.
Уч.с.194 № 975(а). Разложите обыкновенную дробь в периодическую:
а)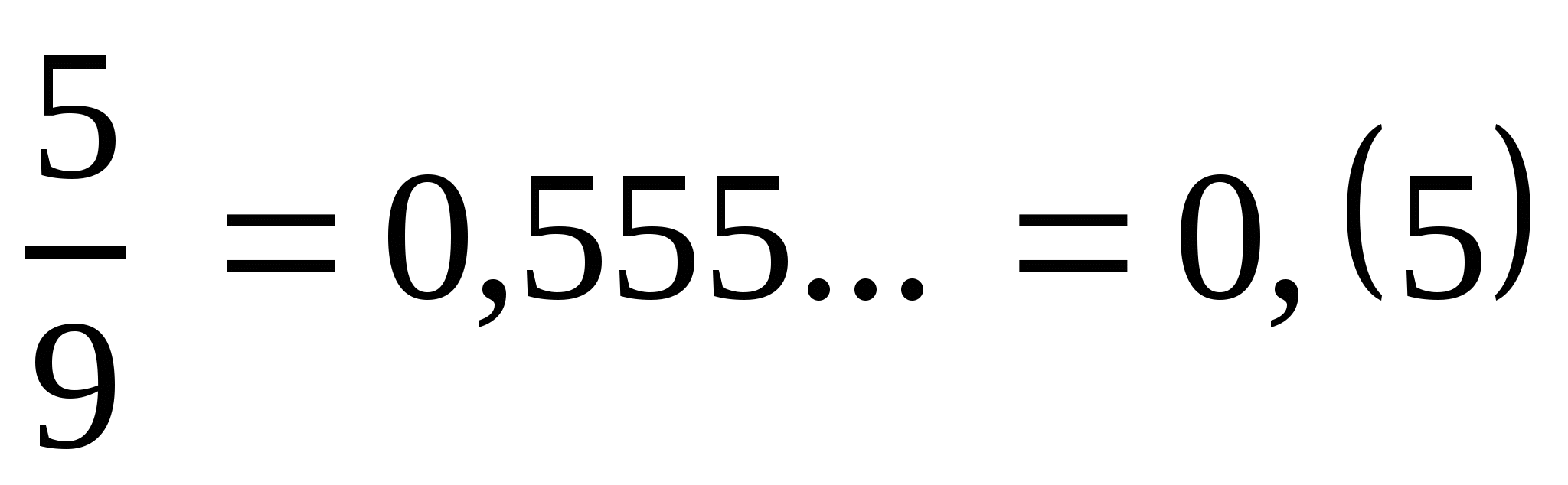 
.
Уч.с.194 № 976(а). Разложите обыкновенную дробь в десятичную и назовите ее период:
а)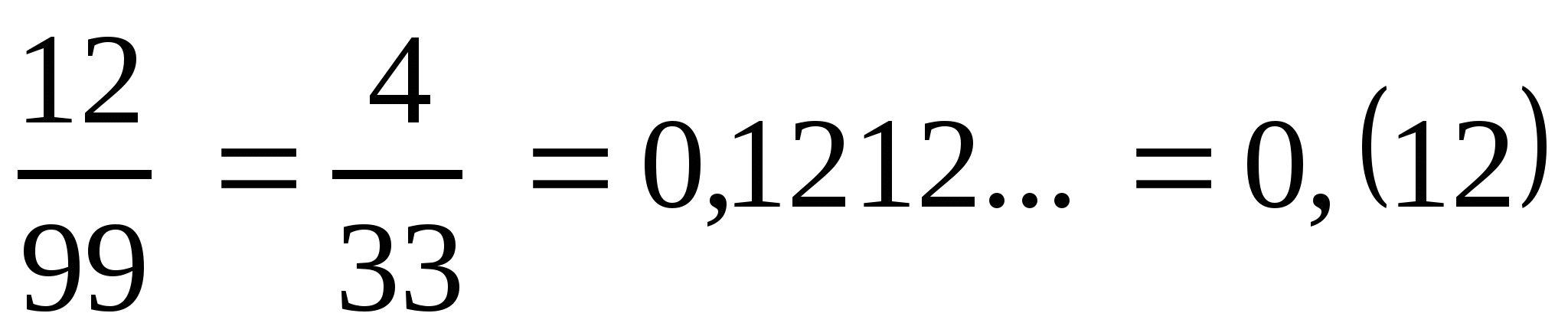 
.
Уч.с.194 № 977(а). Разложите обыкновенную дробь в периодическую:
а)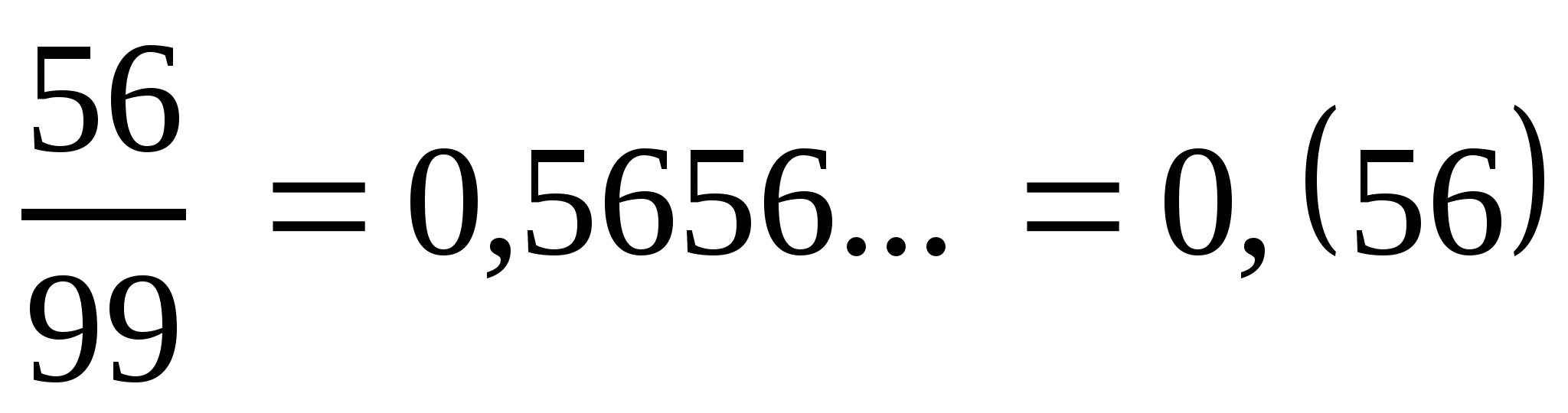 
.