Рассмотрим тонкую пластину толщиной 2h (рис. 9.1), нагруженную только по ее контуру поверхностными силами t1 и t2, симметричными относительно срединной плоскости пластины, с которой совмещена координатная плоскость Ох1х2. При таком нагружении пластины в ее внутренних точках все компоненты тензора напряжений, вообще говоря, будут отличны от нуля и должны удовлетворять трем однородным уравнениям равновесия (принимается, что массовые силы f1 = f2 = f3= 0):
 (9.1)
(9.1)
 (9.2)
(9.2)
Однако по условию нагружения на торцовых плоскостях пластины,
т. е. во всех точках (х1, х2, ± h), должно быть
 (9.3)
(9.3)
Отсюда, в частности, следует, что во всех точках (х1, х2 ± h)
 (9.4)
(9.4)
поэтому из уравнения равновесия (9.2) для этих точек получим
 (9.5)
(9.5)

Рис.9.1
По формуле Тейлора разложим функцию 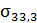 (х1, х2, х3)в ряд по х3, при фиксированных значениях х1 и х2:
(х1, х2, х3)в ряд по х3, при фиксированных значениях х1 и х2:
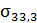 (х1, х2, х3)=
(х1, х2, х3)= 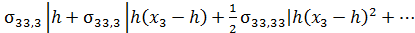
Учитывая (9.3) и (9.5), имеем
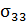 (х1, х2, х3)=
(х1, х2, х3)=  (9.6)
(9.6)
Следовательно, для тонкой пластины компонента 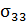 весьма мала и с достаточным приближением можно считать
весьма мала и с достаточным приближением можно считать 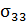 = 0 во всех точках пластины.
= 0 во всех точках пластины.
Остальные компоненты тензора напряжений  представим их средними значениями
представим их средними значениями  по формуле
по формуле
 (9.7)
(9.7)
По условию, пластина нагружена симметрично относительно ее срединной плоскости, поэтому компоненты  — четные функции относительно x3 компоненты
— четные функции относительно x3 компоненты 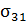 и
и  — нечетные. Отсюда вытекает, что средние значения компонент
— нечетные. Отсюда вытекает, что средние значения компонент 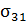 и
и  равны нулю:
равны нулю:
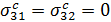 (9.8)
(9.8)
Таким образом, при замене компонент тенора напряжений  их средними значениями
их средними значениями  отличными от нуля и независимыми от х3 будут только три компоненты
отличными от нуля и независимыми от х3 будут только три компоненты  (i = 1, 2; j = 1, 2), т. е. при осреднении компонент тензора напряжений рассматриваемая пластина приближенно будет находиться в плоском напряженном состоянии, которое принято называть обобщенным плоским напряженным состоянием.
(i = 1, 2; j = 1, 2), т. е. при осреднении компонент тензора напряжений рассматриваемая пластина приближенно будет находиться в плоском напряженном состоянии, которое принято называть обобщенным плоским напряженным состоянием.
Поскольку  , уравнения равновесия при использовании средних значений
, уравнения равновесия при использовании средних значений  принимают вид
принимают вид
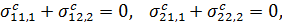 (9.9)
(9.9)
а соотношения закона Гука будут следующими:
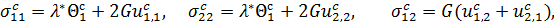
(9.10)
где  - постоянная, определяемая равенствами (7.10);
- постоянная, определяемая равенствами (7.10);
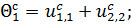 (9.11)
(9.11)
 (9.12)
(9.12)
Так как среднее значение компонент тензора напряжений  не зависят от x3, то уравнения равновесия (9.9) можно удовлетворить введением фукции Эри Ф(x1, x2):
не зависят от x3, то уравнения равновесия (9.9) можно удовлетворить введением фукции Эри Ф(x1, x2):
 (9.13)
(9.13)
Функция  должна подчиняться условиям совместности Бельтрами, а функция Эри, следовательно, должна быть бигармонической.
должна подчиняться условиям совместности Бельтрами, а функция Эри, следовательно, должна быть бигармонической.
Граничные условия для функции Ф(x1, x2) на контуре L пластины выражаются равенствами
 (9.14)
(9.14)
где
 (9.15)
(9.15)
Если на контуре L заданы не внешние силы, а перемещения т. е.
граничные условия
 (9.16)
(9.16)
то в этом случае задачу удобнее решать в перемещениях, используя
уравнения равновесия Ламе, которые для задачи о плоской деформации имеют вид
 (9.17)
(9.17)
а для задачи о плоском напряженном состоянии
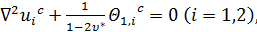 (9.18)
(9.18)
где постоянная  на основании соотношений (7.10)
на основании соотношений (7.10)
 (9.19)
(9.19)
Из сопоставления основных уравнений задачи о плоской деформации с соответствующими уравнениями задачи об обобщенном плавком напряженном состоянии видно, что они математически, идентичны. Заменив в уравнениях первой задачи компоненты  и
и 
 их средними значениями по формуле типа (9.7) а коэффициент Ламе λ — постоянной λ*, определяемой равенствами (7.10), получим уравнения второй задачи. Эти две различные по содержанию задачи сводятся к одной и той же бигармонической краевой задаче, которая называется плоской задачей теории упругости.
их средними значениями по формуле типа (9.7) а коэффициент Ламе λ — постоянной λ*, определяемой равенствами (7.10), получим уравнения второй задачи. Эти две различные по содержанию задачи сводятся к одной и той же бигармонической краевой задаче, которая называется плоской задачей теории упругости.
Приведем еще формулы закона Гука, определяющие деформации
по компонентам тензора напряжений. || *^
В случае плоского напряженного состояния имеем

получим
 (9.20)
(9.20)
В случае плоской деформации

найдем:
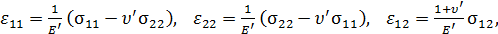 (9.21)
(9.21)
где
 (9.22)
(9.22)
Формулы закона Гука для плоского напряженного состояния и
для плоской деформации можно привести соответственно к следующим видам:

 (9.23)
(9.23)

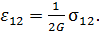 (9.24)
(9.24)
В дальнейшем рассматривается, как правило, задача о плоской деформации, при этом не имеющий значения размер тела вдоль оси х3 принимается равным единице длины. Имея решение задачи о плоской деформации, путем указанной замены получим решение соответствующей задачи об обобщенном плоском напряженном состоянии при тех же граничных условиях.