1. Пусть  – множество европейских государств,
– множество европейских государств,  – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?
– множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?
а) Франция  , б) Испания
, б) Испания  , в) Монголия
, в) Монголия  ,
,
г) Индия  , д) Ирак
, д) Ирак  , е) Турция
, е) Турция  ,
,
ж) Байкал  , з) Волга
, з) Волга  , и) Нигерия
, и) Нигерия  ,
,
к) Гималаи  , л) Япония
, л) Япония  , м) Альпы
, м) Альпы 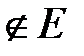 ,
,
н) Швеция  .
.
2. Перечислите элементы каждого из множеств:
а)  ; ;
| |
б)  ; ;
| |
в)  . .
|
3. Задайте с помощью характеристического свойства множество всех положительных чисел.
4. Дано множество  . Составьте подмножества множества
. Составьте подмножества множества  , состоящее из чисел, которые: а) делятся на 4; б) делятся на 9; в) делятся на 5.
, состоящее из чисел, которые: а) делятся на 4; б) делятся на 9; в) делятся на 5.
5. Определите, какой знак из множества {=, ≠, ⊃, ⊂} можно поставить вместо символа «?», чтобы полученное утверждение было верным.
| а) {1, 3}? {1, 2, 3}, б) {2, 3, 4}? {1, 2, 3}, в) {{1, 2}, {2, 3}, {1, 3}}? {1, 2, 3}, г) {{1, 2}, {2, 3}, {1, 3}}? {(1, 2), (2, 3), (1, 3)}, | д) {(2, 1), (3, 2)}? {(1, 2), (2, 3)}, е) {{1, 2}, {2, 3}}? {{2, 1}, {3, 2}, {1, 3}}, ж) {1, 2, 3}? {x|x - делитель 6}, з) ∅? {∅}. |
6. Найдите дополнение к множеству  до множества
до множества  , если
, если
а)  ; б)
; б)  .
.
7. Даны множества:
а) А={0; 1; 2; 3}; B={2;3;4;5}
б) А={x | 2<x≤5}; B={x | 4≤x<6}
в) A=[-2;3); B=(-1;1]
Найдите для каждого случая А∩ В; A∪B; В\ А
8. Задайте множества перечислением их элементов и найти B∩C, A∪B, (A∪B)∩C, A∩B∩C: A – множество делителей числа 12; B={1;5}; C – множество нечетных чисел x таких, что 2<x<13.
9. Изобразить на координатной прямой множества A ∪ В, A ∩ B и A\ B, если:
а) A={x|x∈R и x∈(–1,0]} и B={x|x∈R и x∈[0,2)},
б) A={x|x∈R и x∈(–∞,1]} и B={x|x∈R и x∈(–∞,–3]}.
10. Изобразите на диаграммах Эйлера-Венна такие множества, что:
а) А  В; б) А∩ В=Ø; в) А
В; б) А∩ В=Ø; в) А  В и В
В и В  С; г) А
С; г) А  С, В
С, В  С и А∩ В≠Ø; д) С
С и А∩ В≠Ø; д) С  А, С
А, С  В и С≠A∩B.
В и С≠A∩B.
11. Изобразите с помощью диаграмм Эйлера-Венна отношения включения между множествами  и
и  , если:
, если:
а)  – множество городов северного полушария,
– множество городов северного полушария,  – множество городов, находящихся в Азии;
– множество городов, находящихся в Азии;
б)  – множество городов Африки,
– множество городов Африки,  – множество населенных пунктов Южного полушария;
– множество населенных пунктов Южного полушария;
в)  – множество квадратов,
– множество квадратов,  – множество прямоугольных треугольников;
– множество прямоугольных треугольников;
г)  – множество квадратов,
– множество квадратов,  – множество прямоугольников с равными сторонами.
– множество прямоугольников с равными сторонами.
12. С помощью диаграмм Эйлера – Венна проиллюстрировать справедливость соотношения 
13.

|

|

|

|

|

|

|

|

|
Даны множества
 . Расположите их как показано на диаграммах Эйлера-Венна и для каждого случая заштрихуйте множества: а)
. Расположите их как показано на диаграммах Эйлера-Венна и для каждого случая заштрихуйте множества: а) 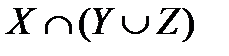 ; б)
; б) 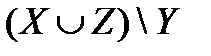 ; в)
; в) 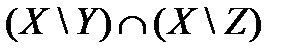 ; г)
; г)  .
.
14. Запишите декартово произведение множеств А×В, если:
а) А={1; 3; 5; 7}; B={2;4;6}; б) А={а;б;в;г}; B={8;9}; в) А={белая; зеленая; желтая}; B={ночь; трава; вода}
15. Запишите множества А и В, если: а) А×В={(3; x); (3; x2); (3; x3)}; б) А×В={(a;a); (a; b); (c;a); (c;b)}.
16. Изобразите на координатной плоскости декартово произведение множеств А и В, если:
a) A = {2; 6}; B ={1;4}, б) А = {2; 6}; В = [1,4], в) А = [2, 6]; B =[1,4]; г) А=R, В=[1;4].
17. Социологи опросили 35 учащихся 8 класса и выяснили, что 20 из них посещают спортивные секции, 11 – факультативы, 10 учащихся не посещают ни факультативы, ни спортивные секции. Сколько учащихся этого класса посещают и факультативы, и спортивные секции?
18. В классе 30 учащихся, 16 из них занимаются музыкой, 17 увлекаются теннисом, а 10 занимаются и музыкой, и теннисом. Есть ли в классе ученики, равнодушные и к музыке, и к теннису?
19. В группе 40 студентов. Из них 23 любят болтать на занятиях, 13 – решать задачи, 11 любят на занятиях спать. Среди тех, кто болтает на занятиях, постоянно засыпают 7, а среди тех, кто решает задачи, засыпают только 3. Болтать и решать задачи умеют 8 человек, а 2 человека умеют на одной паре делать все три дела. Сколько студентов вообще ничего не любят?
20. На загородную прогулку поехали 92 студента. Бутерброды с колбасой взяли 48 студентов, с сыром – 38, с ветчиной – 42, с сыром и колбасой – 28, с колбасой и ветчиной – 31, с сыром и ветчиной – 26 человек.25 студентов взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
21. Каждый ученик класса либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок и одна блондинка любит математику. Всего в классе 24 ученика-блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
22. В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек. По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 8 человек, по геометрии и тригонометрии –9 человек. Ни одной задачи не решили 3 человека.
1) Сколько учащихся решили все задачи?
2) Сколько учащихся решили только две задачи?
3) Сколько учащихся решили только одну задачу?