Контрольная работа №2
по дисциплине «Компьютерные информационные технологии».
выполнила:
студентка 2 курса
группы ЗФК-18
№ зач. книжки 081723
Насонова О.В.
проверил (а):
Витебск
Содержание:
1. Задание 1.
2. Задание 2.
3. Задание 3.
4. Задание 4.
5. Приложение
6. Список использованной литературы.
Задание 1. Используя компьютерные технологии, провести корреляционно-регрессионный анализ исследуемых экономических показателей и построить регрессионную модель.
В качестве инструментария исследования использовать:
функции категории «Статистические» ТП MS Excel,
инструменты надстройки Пакет Аализа ТП MS Excel,
встроенные функции библиотеки Stats (Statistics) CKM Maple.
Условия задания 1:
• По выборочным данным исследовать влияние факторов X1, X2 и Х3 на результативный признак Y.
• Построить корреляционное поле и сделать предположение о наличии и типе связи между исследуемыми факторами;
• Оценив тесноту связи между исследуемыми факторами, построить многофакторную (однофакторную) линейную регрессионную модель вида Y=f(X1,X2 Х3)или вида Y=f(X).
• Оценить:
адекватность уравнения регрессии по значению коэффициента детерминированности R2;
значимость коэффициентов уравнения регрессии по t- критерию Стьюдента при заданном уровне доверительной вероятности р=0,05;
степень случайности связи между каждым факторам Х и признаком Y (критерий Фишера);
• Зависимость между показателями Х1, Х2, Х3основных фондов и объемом валовой продукции У предприятия одной из отрослей промышленности характеризуется следующими данными:
Вариант 4
| X1 | 1.1 | 2.3 | 3.5 | 4.1 | 5.7 | 6.6 | 7.3 | 8.5 | 9.8 | 10.1 | 12.0 |
| X2 | 1.2 | 2.8 | 3.4 | 4.6 | 5.2 | 6.4 | 7.8 | 8.3 | 9.1 | 9.9 | 10.5 |
| X3 | 1.4 | 2.6 | 3.2 | 4.8 | 5.6 | 6.3 | 7.7 | 8.1 | 9.5 | 10.2 | 11.3 |
| Y |
Решение задания 1.
Решение задания 1 предполагает.
1. Построение корреляционного поля.
2. Построение матрицы коэффициентов парной корреляции.
3. Построение и анализ однофакторных регрессионных моделей линейного и экспонентного вида средствами встроенных функций ТП MS Excel.
4. Построение линейных однофакторных регрессионных моделей средствами надстройки «Пакет анализа».
5. Выводы.
Построение корреляционного поля.
Разместим таблицу с исходными данными в ячейках A3:D15 рабочего листа Excel.
| Y | X1 | X2 | X3 |
| 1,2 | 1,2 | ||
| 2,8 | 1,8 | ||
| 3,4 | |||
| 4,6 | 2,5 | ||
| 5,2 | |||
| 6,4 | 3,2 | ||
| 7,8 | 3,5 | ||
| 8,3 | 4,9 | ||
| 9,1 | |||
| 9,9 | 6,2 | ||
| 10,5 | 7,3 | ||
| ? |
| Приложение1.1 | |||
| Y | X1 | X2 | X3 |
| 1,1 | 1,2 | 1,4 | |
| 2,3 | 2,8 | 2,6 | |
| 3,5 | 3,4 | 3,2 | |
| 4,1 | 4,6 | 4,8 | |
| 5,7 | 5,2 | 5,6 | |
| 6,6 | 6,4 | 6,3 | |
| 7,3 | 7,8 | 7,7 | |
| 8,5 | 8,3 | 8,1 | |
| 9,8 | 9,1 | 9,5 | |
| 10,1 | 9,9 | 10,2 | |
| 10,5 | 11,3 | ||
| ? |
Используя возможности мастера диаграмм ТП MS Excel, построим корреляционное поле, то есть представим графически связь между результирующим признаком Y и каждым из факторов X. Из графиков видно, что между результирующим признаком Y и каждым из факторов X существует прямо пропорциональная зависимость, приближающаяся к линейной.
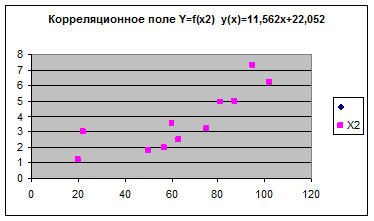
Исследуем тесноту и характер связи между факторами.
Построение матрицы коэффициентов парной корреляции.
Используя надстройку «Пакет анализа» ТП MS Excel (Сервис – Анализ данных – Корреляция), построим матрицу коэффициентов парной корреляции. Окно инструмента «Корреляция» представлено на рисунке 1. Матрица коэффициентов парной корреляции представлена на рисунке 2.
Рис.1. –Окно «Корреляция»
| Корреляция | ||||
| Y | X1 | X2 | X3 | |
| Y | ||||
| X1 | 0,841096 | |||
| X2 | 0,826568 | 0,954219 | ||
| X3 | 0,917611 | 0,872999 | 0,89252 |
Рис.2. – Матрица коэффициентов парной корреляции.
Из этой матрицы видно, что все рассматриваемые факторы X! – X3 имеют тесную связь с результативным признаком Y. Кроме того, все факторы Х между собой мультиколлинеарны. Поэтому построение многофакторной модели вида Y=f(Х1,Х2,Х3) невозможно.
Построение однофакторной регрессионной модели вида Y=f(Х1).
Для построения модели линейного вида Y=m*x+b воспользуемся функцией ЛИНЕЙН из категории статистических функций ТП MS Excel. В ячейки E4:F8 с помощью мастера функций введём как формулу массива функцию ЛИНЕЙН в следующем формате =ЛИНЕЙН(А4:А14;В4:В14;1;1) - для Y=f(Х1), =ЛИНЕЙН(А4:А14;С4:С14;1;1) – для Y=f(X2), =ЛИНЕЙН(А;:А14;D4^D14;1;1) – для Y=f(X3). При вводе следует нажать клавиши <CTRL>,<SHIFT> B <ENTER>. В результате получим массив значений, верхняя строка которого представляет собой коэффициенты уравнения регрессии m и b:
| Линейная | |
| 7,354974 | 18,4578 |
| 1,576592 | 10,95188 |
| 0,707443 | 15,40461 |
| 21,76324 | |
| 5164,462 | 2135,719 |
Таким образом, уравнение регрессии, устанавливающее зависимость между одним из показателей реализованной продукции и балансовой прибылью Y предприятий одной из отраслей промышленности имеет вид
Y(X1)л = 7,355*Х1+18,458
а) коэффициент детерминированности R^2 = 0,707443 (ячейка N22).
б) значимость коэффициентов уравнения регрессии определяется по t-критерию Стьюдента. Расчётное значение критерия Стьюдента tp = 4,655108 (ячейка O27, формула =N20/N21), что больше табличного tт=2,26 (функция = СТЬЮДРАСПОБР (0,05;1;L23). То есть коэффициент при переменной Х1 значим.
в) Расчётное значение критерия Фишера Fp=21,76324 (ячейка N23), больше табличного Fт=5,117 (ячейка О12, формула =FРАСПОБР(0,05;1;L23)). То есть связь между факторами не случайна и в целом уравнение регрессии адекватно.
| Fтабл= | 5,117355 |
| tтабл= | 2,262157 |
Для построения экспоненциальной модели вида Y=b*m^x воспользуемся функцией ЛГРФПРИБЛ и в ячейках К20:L24 в соответствии с описанной выше методикой рассчитаем параметры экспоненциальной регрессионной модели. Получим уравнение регрессии вида
Y(X1)э=24,708*1,145^X1
| Экспоненциальная | |
| 1,144797 | 24,70776 |
| 0,038325 | 0,266224 |
| 0,580422 | 0,374463 |
| 12,45013 | |
| 1,74579 | 1,262004 |
В этой модели коэффициент детерминированности R^2=0,58 (ячейка К22).
Критерий Фишера Fр=12,45 (ячейка К23) больше табличного Fт=5,12. То есть связь между факторами не случайна и в целом уравнение регрессии адекватно.
| Fтабл= | 5,117355 | ||||
| tтабл= | 2,262157 | ||||
| МодельY=f(X1) | |||||
| Экспоненциальная | Линейная | ||||
| 1,144797 | 24,70776 | 7,354974 | 18,4578 | ||
| 0,038325 | 0,266224 | 1,576592 | 10,95188 | ||
| 0,580422 | 0,374463 | 0,707443 | 15,40461 | ||
| 12,45013 | 21,76324 | ||||
| 1,74579 | 1,262004 | 5164,462 | 2135,719 | ||
| Y(X1)э=24,708*1,145^X1 | Y(X1)л=7,355Х1+18,458 | ||||
| tрасч= | 4,665108 |
| Прогноз Y | ||||
| Y(X1)э= | 125,19164 | Y(X1)л= | 106,7175 | |
Аналогичным образом рассчитаем и оценим адекватность уравнения регрессии вида Y=f(X2).
Построение однофакторной регрессионной модели вида Y=f(X2).
В ячейки N38:O42 введём формулу ЛИНЕЙН в следующем формате = ЛИНЕЙН(А4:А14;С4:С14;1;1).
| Линейная | |
| 11,56213 | 22,05249 |
| 2,624345 | 10,82508 |
| 0,683214 | 16,02981 |
| 19,41038 | |
| 4987,589 | 2312,592 |
Уравнение регрессии модели линейного вида:
Y(X2)=11,562Х2+22,052
а) коэффициент детерминированости = 0,683 (ячейка N40).
б) Расчётное значение критерия Стьюдента tр=4,406 (ячейка О45, формула =N38/N39), что больше табличного tт=2,26 (функция= СТЬЮДРАСПОБР(0,05;L41). То есть коэффициент при переменной Х2 значим.
в) Расчётное значение критерия Фишера Fр=19,41 (ячейка N41) больше табличного Fт=5,117 (ячейка О33, формула=FРАСПОБР(0,05;1;L41)). Уравнение регрессии адекватно.
Уравнение регрессии экспоненциальной модели:
Y(X2)э=27,457*1,224^X2
| Экспоненциальная | |
| 1,223726 | 27,45708 |
| 0,066545 | 0,27449 |
| 0,50564 | 0,406466 |
| 9,205356 | |
| 1,520861 | 1,486933 |
В этой модели коэффициент детерминированности R^2=0,506 (ячейка К40).
Критерий Фишера Fр=9,205 (ячейка К41) больше табличного Fт=5,12. Связь между факторами не случайна и в целом уравнение адекватно.
| 5,117355 | |||||
| 2,262157 | |||||
| Модель | Y=f(X2) | ||||
| Экспоненциальная | Линейная | ||||
| 1,223726 | 27,45708 | 11,56213 | 22,05249 | ||
| 0,066545 | 0,27449 | 2,624345 | 10,82508 | ||
| 0,50564 | 0,406466 | 0,683214 | 16,02981 | ||
| 9,205356 | 19,41038 | ||||
| 1,520861 | 1,486933 | 4987,589 | 2312,592 | ||
| Y(X2)э=27,457*1,224^X2 | Y(X2)=11,562X2+22,052 | ||||
| tрасч= | 4,405722 |
| Прогноз Y | ||||
| Y(X2)э= | 138,07927 | Y(X2)л= | 114,5496 | |
Построение однофакторной регрессионной модели вида Y=f(X3).
В ячейки N55:O59 введём как формулу массива функцию ЛИНЕЙН в следующем формате =ЛИНЕЙН(А4:А14;D4:D14;1;1).
| Линейная | |
| 7,735398 | 21,83097 |
| 1,116907 | 7,071963 |
| 0,84201 | 11,32035 |
| 47,96576 | |
| 6146,829 | 1153,353 |
Уравнение регрессии линейного вида:
Y(X3)л=7,735Х3+21,831
а) коэффициент детерминированности R^2=0,842 (ячейка N57).
б) Расчётное значение критерия Стьюдента tр=6,957 (ячейка О62, формула=N55/N56), что больше табличного tт=2,26 (функция=СТЬЮДРАСПОБР(0,05;L58). То есть коэффициент при переменной Х3 значим.
в) Расчётное значение критерия Фишера Fр=47,986 (ячейка N58) больше табличного Fт=5,117 (ячейка О50, формула=FРАСПОБР(0,05;1;L58)). Связь между факторами не случайна и в целом уравнение регрессии адекватно.
Уравнение регрессии экспоненциальной модели:
Y(X3)э=26,684*1,15^X3
| Экспоненциальная | |
| 1,149736 | 26,68357 |
| 0,033015 | 0,209044 |
| 0,664951 | 0,334624 |
| 17,86176 | |
| 2,000036 | 1,007758 |
В этой модели коэффициент детерминированности R^2=0,665 (ячейка К57).
Критерий Фишера Fр=17,862 (ячейка К58) больше табличного Fт=5,12. То есть связь между факторами не случайна и в целом уравнение регрессии адекватно.
| 5,117355 | ||||
| 2,262157 | ||||
| Модель | Y=f(X3) | |||
| Экспоненциальная | Линейная | |||
| 1,149736 | 26,68357 | 7,735398 | 21,83097 | |
| 0,033015 | 0,209044 | 1,116907 | 7,071963 | |
| 0,664951 | 0,334624 | 0,84201 | 11,32035 | |
| 17,86176 | 47,96576 | |||
| 2,000036 | 1,007758 | 6146,829 | 1153,353 | |
| Y(X3)э=26,684*1,15^X3 | Y(X3)=7,735Х3+21,831 | |||
| tрасч= | 6,925732 |
| ПрогнозY | ||||
| Y(X3)э= | 188,20014 | Y(X3)л= | 130,1265 |
Построение линейной однофакторной регрессионной модели Y=f(X1) средствами надстройки «Пакет анализа».
Используя надстройку «Пакет анализа» ТП MS Excel (Сервис – Анализ данных – Регрессия), рассчитаем линейную регрессионную модель вида Y=f(x1).
Рис3-Окно «Регрессия»
Результаты регрессионного анализа (ячейки Q16:Y33) представлены в виде трёх таблиц.
Первая таблица – «Регрессионная статистика» (ячейки Q18:R23) позволяет оценить тесноту связи между факторами и уровень стандартной ошибки).
| ВЫВОД ИТОГОВ Y=f(X1) | |||
| Регрессионная статистика | |||
| Множественный R | 0,841096 | ||
| R-квадрат | 0,707443 | ||
| Нормированный R-квадрат | 0,674937 | ||
| Стандартная ошибка | 15,40461 | ||
| Наблюдения |
Вторая таблица – «Дисперсионный анализ» на основании критерия Фишера, остаточной и регрессионной суммы квадратов позволяет оценить адекватность уравнения регрессии в целом.
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 5164,462 | 5164,462 | 21,76324 | 0,001177 | ||
| Остаток | 2135,719 | 237,3021 | ||||
| Итого | 7300,182 |
В третьей таблице представлены значения коэффициентов уравнения регрессии (ячейки R32:R33), критерий Стьюдента (ячейки Т32:Т33) и уровень значимости р (ячейки U32:U33).
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | ||
| Y-пересечение | 18,4578 | 10,95188 | 1,685355 | 0,126202 | -6,31707 | 43,23266 | -6,31707 | 43,23266 | |
| X1 | 7,354974 | 1,576592 | 4,665108 | 0,001177 | 3,788475 | 10,92147 | 3,788475 | 10,92147 |
Результаты расчёта, проведённого с помощью надстройки «Пакет анализа», полностью совпадают с результатами, возращёнными функцией ЛИНЕЙН и в дополнительных комментариях не нуждаются.
Аналогично проводим регрессионный анализ для линейной модели вида Y=f(X2).
| ВЫВОД ИТОГОВ Y=f(X2) | ||||||||||||||||||||
| Регрессионная статистика | ||||||||||||||||||||
| Множественный R | 0,826568 | |||||||||||||||||||
| R-квадрат | 0,683214 | |||||||||||||||||||
| Нормированный R-квадрат | 0,648016 | |||||||||||||||||||
| Стандартная ошибка | 16,02981 | |||||||||||||||||||
| Наблюдения | ||||||||||||||||||||
| Дисперсионный анализ | ||||||||||||||||||||
| df | SS | MS | F | Значимость F | ||||||||||||||||
| Регрессия | 4987,589 | 4987,589 | 19,41038 | 0,001706 | ||||||||||||||||
| Остаток | 2312,592 | 256,9547 | ||||||||||||||||||
| Итого | 7300,182 | |||||||||||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |||||||||||||
| Y-пересечение | 22,05249 | 10,82508 | 2,037166 | 0,072095 | -2,43555 | 46,54052 | -2,43555 | 46,54052 | ||||||||||||
| X2 | 11,56213 | 2,624345 | 4,405722 | 0,001706 | 5,625453 | 17,49882 | 5,625453 | 17,49882 | ||||||||||||
Проводим регрессионный анализ для линейной модели вида Y=f(X3).
| ВЫВОД ИТОГОВ | |||
| Регрессионная статистика | |||
| Множественный R | 0,917611 | ||
| R-квадрат | 0,84201 | ||
| Нормированный R-квадрат | 0,824456 | ||
| Стандартная ошибка | 11,32035 | ||
| Наблюдения |
| Дисперсионный анализ | ||||||||||||||||
| df | SS | MS | F | Значимость F | ||||||||||||
| Регрессия | 6146,829 | 6146,829 | 47,96576 | 6,87E-05 | ||||||||||||
| Остаток | 1153,353 | 128,1503 | ||||||||||||||
| Итого | 7300,182 | |||||||||||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |||||||||
| Y-пересечение | 21,83097 | 7,071963 | 3,086975 | 0,012993 | 5,833082 | 37,82886 | 5,833082 | 37,82886 | ||||||||
| X3 | 7,735398 | 1,116907 | 6,925732 | 6,87E-05 | 5,208779 | 10,26202 | 5,208779 | 10,26202 | ||||||||
Вывод: все построенные модели отвечают условиям адекватности. Наиболее высокие статистические характеристики имеет модель Y=f(X3) вида:
Y=26,684*1,15^x, в которой
коэффициент детерминированности R^2=0,665;
критерий Фишера F=17,862 (Fp=17,862>Fт=5,117)
критерий Стьюдента =6,93 (tp=6,93>tт=2,26) коэффициенты уравнения значимы.
Решение задания с помощью встроенных функций библиотеки Stats (Statistics) CKM Maple.
> restart;
> with(stats);
> X1:=[1.2,2.8,3.4,4.6,5.2,6.4,7.8,8.3,9.1,9.9,10.5];
> X2:=[1.2,1.8,2.0,2.5,3.0,3.2,3.5,4.9,5.0,6.2,7.3];
> X3:=[2,3,4,3,2,6,5,7,8,12,9];
> Y:=[20,50,57,63,22,75,60,81,87,102,95];
> fit[leastsquare[[x1,x2,x3,y]]]([X1,X2,X3,Y]);
> correl:=evalf(describe[linearcorrelation](X1,Y),4);
> correl:=evalf(describe[linearcorrelation](X2,Y),4);
> correl:=evalf(describe[linearcorrelation](X3,Y),4);
> spisok:=(x,y)->[x,y];
> f:=fit[leastsquare[[x,y]]]([X3,Y]);
> k:=zip(spisok,X3,Y);
> fun:=rhs(f);
> for i from 1 to nops(X3) do
Y1[i]:=evalf(subs({x=X3[i]},fun))
end do:
> Y1:=convert(Y1,list);
> k1:=zip(spisok,X3,Y1):
> plot([k,k1],thickness=3,labels=["X3", "Y"],labeldirections
=[horizontal,vertical],legend=[" Исходныеданные ",
" теоретич. модель "],title=cat(" модель Y=",convert(evalf(fun,
7),string)));
модель Y=21.83097+7.735398*x
+
+
100 + BBBB
+ BBBB
80 + BBBBB
+ BBBBB
60 + BBBB
+ BBBB
40 + BBBBB
+
20 +
+
***************************************************************************
-8 -4 4 8
AAAAAAAAAAAAAAAA Исходные данные
BBBBBBBBBBBBBBBB теоретич.модель
> y:=convert(Y,array);
> n:=nops(Y):sr:=evalf((sum(y[j],j=1..n)/n),7);
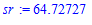
> Q:=evalf((sum((y[j]-sr)^2,j=1..n)),12);
> y1:=convert(Y1,array):
> Qe:=evalf((sum((y[j]-y1[j])^2,j=1..n)),12);
> Qr:=evalf((sum((y1[j]-sr)^2,j=1..n)),12);
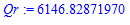
> R:=evalf(Qr/(Qr+Qe),4);
> correl:=(R^0.5,6);
> k:=1;
> S:=Qe/(n-k-1);
> F:=evalf(Qr/S,4);
> printf(" Коэффициент} корреляции-->%20.6f\nКоэффициент} детерминированности} -->%22.8f\n",correl,R):
printf("Регрессионная} сумма} квадратов}-->%15.1f\nОстаточная сумма} квадратов}-->%15.1f\n",Qr,Qe):
printf("Общая} сумма} квадратов}-->%15.1f\nКритерий Фишера-->%16.2f\n",Q,F);
Коэффициент} корреляции--> 0.917660
Коэффициент} детерминированности} --> 6.00000000
Регрессионная} сумма} квадратов}--> 6146.8
Остаточная сумма} квадратов}--> 1153.4
Общая} сумма} квадратов}--> 7300.2
Критерий Фишера--> 47.95
Задание 2. Используя компьютерные технологии, решить задачи линейного программирования.
а) Задача оптимального планирования производства
Условие задания 2а): Для производства двух видов изделий А и В используется три типа технологического оборудования. На производство единицы изделия А оборудование первого типа используется а1 часов, оборудование второго типа – а2 часов, оборудование третьего типа – а3 часов. На производство единицы изделия В оборудование первого типа используется в1 часов, оборудование второго типа – в2 часов, оборудование третьего типа – в3 часов.
На изготовление всех изделий администрация предприятия может предоставить оборудование первого типа не более чем на t1 часов, оборудование второго типа не более чем на t2 часов, оборудование третьего типа не более чем на t3 часов. Прибыль от реализации единицы готового изделия А составляет α руб., а изделия В – β руб.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
В качестве инструментария решения использовать:
надстройку «Поиск решения» ТП MS Excel,
библиотеки Simplex и Optimization СКМ Maple
| Вариант | а1 | а2 | а3 | в1 | в2 | в3 | t1 | t2 | t3 | α | β |
б) Задача оптимизации плана перевозок (транспортная задача)
Условие задания 2б): Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения cijприведена в таблице, где под строкой понимается пункт производства, а под столбцом – пункт распределения. Кроме того, в этой таблице в i-той строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы. Номер таблицы с исходными данными соответствует номеру варианта.
В качестве инструментария решения использовать: (на выбор из перечисленных ниже):
надстройку «Поиск решения» ТП MS Excel,
библиотеку Simplex СКМ Maple,
библиотеку Optimization СКМ Maple
Вариант 3
| Стоимость перевозки единицы продукции | Объёмы производства | ||||
| Объёмы потребления |
Решение задания 2.
а).
Решение задания 2 предполагает:
1. Математическую постановку задачи.
2. Размещение на рабочем листе ТП MS Excel исходных данных, расчёт значений ограничений, расчёт значений целевой функции.
3. Формулировка математической модели задачи в терминах ячеек рабочего листа ТП MS Excel.
4. Поиск оптимального решения поставленной задачи средствами надстройки «Поиск решения».
5. Анализ результатов.
Математическая постановка задачи
Обозначим через х1 – количество изделий вида А;
х2 – количество изделий вида В.
Математическая модель задачи имеет вид:
Целевая функция: F=6х1+3х2--max
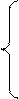Система ограничений:
4x1+3x2<=520
6x1+2x2<=600
3x1+4x2<=600
x1,x2>=0, x1,x2-целое
Размещение данных на рабочем листе ТП MS Excel
Разместим исходные данные в ячейках А3:F6 рабочего листа ТП MS Excel как показано на рисунке 2.
| Решение: | |||||
| Вид продукции | Время обработки,ч | Прибыль,у.е. | Количество | ||
| А | |||||
| В | |||||
| =E5*F5+E6*F6 | |||||
| Время | =B5*$F$5+B6*$F$6 | =C5*$F$5+C6*$F$6 | =D5*$F$5+D6*$F$6 | ||
| Ограничения |
Таблица 2.1 - Исходные данные в режиме формул
В ячейки F5:F6 внесём начальное значение параметров х1 и х2 (примем их равным нулю).
В ячейки B9:D9 внесём значения ограничений на использование оборудования каждого вида 600, 520 и 600 соответственно.
В ячейках B8:D8 рассчитаем значения ограничений на использование оборудования каждого вида соответственно (формулы показаны на рисунке 1).
В ячейке Е7 рассчитаем значение целевой функции.
| Решение: | |||||
| Вид продукции | Время обработки,ч | Прибыль,у.е. | Количество | ||
| А | |||||
| В | |||||
| Время | |||||
| Ограничения |
Таблица 2.2 - Исходные данные к задаче
Формулировка математической модели задачи в терминах ячеек рабочего листа ТП MS Excel
Целевая функция: ячейка Е7—7
Система ограничений:
B8<=B9
C8<=C9
D8<=D9
F5:F6>=0, F5:F6-целое
Таким образом, в терминах ячеек рабочего листа ТП MS Excel математическая модель задачи может быть сформулирована следующим образом:
добиться максимального значения в ячейке Е7, изменяя значения ячеек F5:F6 так, чтобы значения в ячейках B8:D8 были бы не больше значений в ячейках B9:D9 при неотрицательных и целых значениях в ячейках F5:F6.
Поиск оптимального решения
Окно надстройки «Поиск решения» (Сервис-Поиск решения) с постановкой задачи в терминах ячеек рабочего листа Excel приведены ниже:
Рис. 2.1 – Окно надстройки «Поиск решения»
| Решение | |||||
| Вид | Время обработки, ч | Прибыль, у.е | Количество | ||
| продукции | I | II | III | ||
| А | |||||
| В | |||||
| Время | |||||
| Ограничения | |||||
| Исходно: | |||||
| Вид | Время обработки, ч | Прибыль, у.е | Количество | ||
| продукции | I | II | III | ||
| А | |||||
| В | |||||
| Время | |||||
| Ограничения | |||||
Таблица 2.3 - Решение задания в режиме значений.
| Решение | |||||
| Вид | Время обработки, ч | Прибыль, у.е | Количество | ||
| продукции | I | II | III | ||
| А | |||||
| В | |||||
| =E5*F5+E6*F6 | |||||
| Время | =B5*$F$5+B6*$F$6 | =C5*$F$5+C6*$F$6 | =D5*$F$5+D6*$F$6 | ||
| Ограничения | |||||
| Исходно: | |||||
| Вид | Время обработки, ч | Прибыль, у.е | Количество | ||
| продукции | I | II | III | ||
| А | |||||
| В | |||||
| =E16*F16+E17*F17 | |||||
| Время | =B16*$F$16+B17*$F$17 | =C16*$F$16+C17*$F$17 | =D16*$F$16+D17*$F$17 | ||
Ограниче
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-02 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |