ЛАБОРАТОРНАЯ РАБОТА № 10
ИНТЕГРИРОВАННАЯ СИСТЕМА STATISTICA.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ

Цель работы: Приобрести практические навыки проведения корреляционного анализа с помощью специализированных модулей интегрированной системы (ИС) STATISTICA.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общие сведения
Совокупность методов оценки корреляционных характеристик и проверка статистических гипотез о них по выборочным данным называется корреляционным анализом. В корреляционном анализе используются следующие основные приемы:
1) построение корреляционного поля (диаграммы рассеяния) для двух экономических показателей или двумерных сечений, если речь идет о большем их количестве;
2) определение выборочных коэффициентов корреляции или составление корреляционных матриц;
3) проверка статических гипотез о значимости связи между показателями.
Коэффициент корреляции оценивает тесноту связи между исследуемыми переменными и является мерой линейной зависимости величин.
Если оценивается связь между двумя любыми количественными переменными, используется парный коэффициент корреляции. Для оценки тесноты связи между результирующим показателем и совокупностью входных факторов используется множественный коэффициент корреляции. Для оценки тесноты связи между качественными (порядковыми) переменными используется ранговый коэффициент корреляции.
Этот коэффициент, всегда обозначаемый латинской буквой r, может принимать значения между -1 и +1, причём если значение находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0, то слабой.
Если коэффициент корреляции отрицательный, это означает наличие противоположной связи: чем выше значение одной переменной, тем ниже значение другой. Сила связи характеризуется также и абсолютной величиной коэффициента корреляции. Для словесного описания величины коэффициента корреляции используются следующие градации (см. таблица 10.1).
Таблица 10.1. Градации коэффициента корреляции
| Значение | Интерпретация |
| до 0,2 | Очень слабая корреляция |
| до 0,5 | Слабая корреляция |
| до 0,7 | Средняя корреляция |
| до 0,9 | Высокая корреляция |
| свыше 0,9 | Очень высокая корреляция |
Ориентировочно определить величину коэффициента корреляции можно, анализируя диаграмму рассеяния. Чем теснее расположены точки относительно некоторой прямой, тем больше по абсолютной величине он стремится к единице, и наоборот, чем более расплывчата диаграмма рассеяния, тем ближе к нулю коэффициент корреляции.
Модуль Basic Statistics/Tables ИС STATISTICA
Статистические процедуры системы STATISTICA сгруппированы в нескольких специализированных статистических модулях. В каждом модуле можно выполнить определенный способ обработки данных, не обращаясь к процедурам из других модулей.
Работа в системе STATISTICA начинается обычно с модуля BasicStatistics / Tables (Основные статистики/Таблицы). С его помощью можно провести предварительную обработку данных, осуществить разведочный анализ данных, определить зависимости между ними, разбить их различными способами на группы, просмотреть эти группы визуально и определить взаимосвязи между данными. Этот статистический модуль включает в себя различные группы статистических процедур, реализующих методы разведочного статистического анализа. Система может вычислить практически все описательные статистики, включая медиану, моду, квартили, средние и стандартные отклонения, доверительные интервалы для среднего, коэффициенты асимметрии, эксцесса (с их стандартными ошибками), гармоническое и геометрическое среднее, а также многие другие описательные статистики. Широкий выбор графиков позволяет проиллюстрировать проведенный разведочный анализ данных.
Подраздел Корреляциивключает большое количество средств, позволяющих исследовать зависимости между переменными. Возможно вычисление практически всех общих мер зависимости, включая коэффициент корреляции Пирсона, коэффициент ранговой корреляции Спирмена, коэффициент сопряженности признаков и многие другие. Корреляционные матрицы могут быть вычислены и для данных с пропусками, используя специальные методы обработки пропущенных значений.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задание 1. Проанализировать показатели хозяйственной деятельности предприятий легкой промышленности [7]. Построить корреляционную матрицу, дать графическую интерпретацию результатов. В качестве исходных данных использовать данные из таблицы П1 Приложения 1.
Y1 – производительность труда, млн. руб.;
X1 – трудоёмкость единицы продукции, час.;
X2 – удельный вес рабочих в составе ППП;
X3 – удельный вес комплектующих изделий;
X4 – коэффициент сменности оборудования;
X5 – премии и вознаграждения на одного работника, млн. руб.;
X6 – удельный вес потерь от брака в себестоимости продукции, %;
X7 – фондоотдача, руб.;
X8 – среднесписочная численность ППП;
X9 – среднегодовая стоимость ОПС, млрд. руб.;
X10 – фонд з/п ППП, млн. руб.;
X11 – фондовооруженность труда, млн. руб.;
X12 – оборачиваемость нормируемых оборотных средств;
X13 – оборачиваемость ненормируемых оборотных средств;
X14 – непроизводительные расходы.
Проведем корреляционный анализ переменных X1, X3, X7.
Для проведения корреляционного анализа необходимо выбрать модуль Basic Statiatics/Tables и далее пункт Correlation matrices (Корреляционные матрицы).
В появившемся окне Pearson Product-Moment Correlation (Корреляция Пирсона) (рис.10.1), нажав кнопку Twolists(Двасписка), следует определить, какие переменные будут находиться в строках (First variable list) – это переменные X1, X3, X7 и в столбцах (Second variable list) – это переменная Y (рис.10.2).

Рис. 10.1– Окно Pearson Product-Moment Correlation
Для подтверждения выбора и возврата в окно Pearson Product-Moment Correlation нажать ОК.
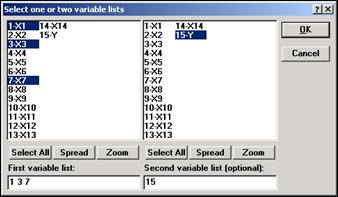
Рис.10.2 – Окно Select one or two variable list
В окне Pearson Product-Moment Correlationтакжеследует нажать кнопку ОК. На экране появится корреляционная матрица (рис.10.3).

Рис.10.3 – Корреляционная матрица
В этой матрице имеется только один столбец, так как во втором списке мы выбрали только одну переменную. В столбце даны коэффициенты корреляции между переменными Y и X1, X3, X7. Красным цветом автоматически выделены коэффициенты, значимые на уровне p<0,05. Именно на эти коэффициенты следует обратить наибольшее внимание. В рассматриваемом примере переменная Y наиболее зависима от переменных X1 (коэффициент корреляции -0,82) и X3 (коэффициент корреляции 0,64).
Чтобы построить корреляционную матрицу, отражающую тесноту связи между всеми переменными, следует в окне Pearson Product-Moment Correlationнажать кнопкуOne variable listи выбрать переменные Y, X1, X3 и X7. Затем вернуться в окно Pearson Product-Moment Correlationинажать кнопкуОК.В результате на экране появится корреляционная матрица, отражающая все парные коэффициенты корреляции для рассматриваемых переменных (см. рис.10.4). Красным цветом в ней автоматически выделены коэффициенты, значимые на уровне p<0,05.

Рис.10.4 – Корреляционная матрица
Для построения графического отображения корреляционной взаимосвязи любых двух переменных необходимо нажать кнопку 2D scatterplot (диаграмма рассеяния) в окне Pearson Product-Moment Correlationи определить, какие переменные будут расположены по горизонтальной и вертикальной оси. Построим диаграмму рассеяния для переменных Y и X1 (см. рис. 10.5).

| Рис. 10.5 – Диаграмма рассеяния | Рис.10.6 – Диаграмма рассеяния |
| для переменных Y и X1 | для переменных Y и X7 |
Для сравнения аналогичным образом построим диаграмму рассеяния для переменных Y и X7 (см. рис. 10.6).
В этом случае из графика видно, что зависимость нельзя признать линейной. Можно попробовать графически подобрать вид зависимости. Для этого в меню Graphs следует выбрать команду Stats 2D Graph, затем команду Scatterplots, после чего в окне Scatterplots (см. рис. 10.7) кнопкой Variables определить исследуемые переменные и выбрать вид зависимости, например полиномиальную.

Рис.10.7 – Окно Scatterplots
В результате на экране появится диаграмма рассеяния (см. рис. 10.8), построенная на базе полинома пятой степени. Интересным является факт, что степень полинома (максимальной является пятая степень) STATISTICA определяет сама в зависимости от исходного набора данных.
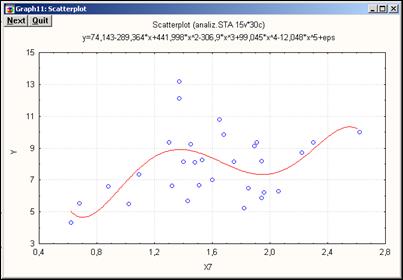
Рис. 10.8 – Диаграмма рассеяния для переменных Y и X7
при аппроксимации полиномом
Как и на рисунке 10.5, на этом графике (рис. 10.8) представлены функция, отражающая взаимосвязь переменных Y и X7, и корреляционное поле точек. Из графика отчетливо видно, что и полином пятой степени не описывает должным образом исходные данные. В этом случае следует воспользоваться упомянутым выше модулем Nonlinear Estimation, предоставляющим возможность пользователю создавать собственные функции для аппроксимации исследуемых данных.
Чтобы оценить все связи визуально, можно представить корреляционную матрицу в графическом виде (см. рис. 10.9). Для этого в окне PearsonProduct-Moment Correlationследует нажать кнопку Matrix, затем выбрать все переменные нажатием кнопки Select All и подтвердить выбор нажатием OК.
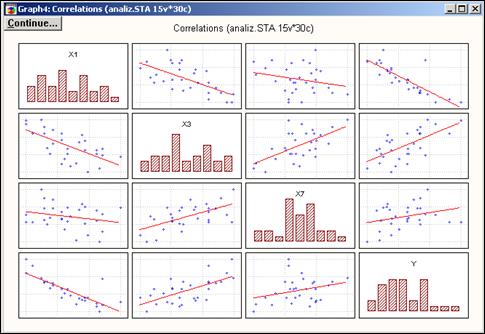
Рис. 10.9 – Корреляционная матрица в графическом представлении
Для получения числовых характеристик (описательной статистики) изучаемых признаков в стартовой панели модуля Basiс Statistics необходимо выбрать раздел Decriptive Statistics и нажать ОК. Кнопкой Variables выбрать переменные, для которых требуется получить числовые характеристики (рис. 10.10), затем, нажав кнопку More statistics, определить, какие характеристики должны быть рассчитаны, и нажать ОК.

Рис. 10.10 – Окно Decriptive Satistics
Выберем числовые характеристики, характеризующие распределение переменных: среднее значение (Mean), медиану (Median), дисперсию (Variance), коэффициенты асимметрии (Skewness) и эксцесса (Kurtosis). Далее следует нажать кнопку Detailed decriptive statisticsи получить результат (см. рис. 10.11).

Рис.10.11– Описательная статистика переменных X1, X3, X7 и Y
Как видно из таблицы на рис. 10.11, распределение переменных близко к нормальному.
Задания для самостоятельной работы 
Задание 1. По выборочным данным (таблица 10.2) исследовать влияние факторов X1, X2 и Х3на результативный признак Y.
Построив корреляционное поле, сделать предположение о наличии и типе связи между исследуемыми факторами.
Таблица 10.2. Показатели деятельности предприятия
| Номер предприятия | Выработка продукции на одного работника тыс. руб. | Новые ОПФ, % | Удельный вес рабочих высокой квалификации % | Коэффициент использования оборудования |
| № | Y | x1 | x2 | x3 |
| 3,9 | 0,76 | |||
| 3,9 | 0,78 | |||
| 3,7 | 0,75 | |||
| 0,78 | ||||
| 3,8 | 0,74 | |||
| 4,8 | 0,81 | |||
| 5,4 | 0,81 | |||
| 4,4 | 0,82 | |||
| 5,3 | 0,82 | |||
| 6,8 | 0,82 | |||
| 0,84 | ||||
| 6,4 | 0,84 | |||
| 6,8 | 0,8 | |||
| 7,2 | 0,8 | |||
| 0,85 | ||||
| 8,2 | 0,85 | |||
| 8,1 | 0,88 | |||
| 8,5 | 0,87 | |||
| 9,6 | 0,89 | |||
| 0,85 |
Варианты заданий
Варианты 1-4: результативный признак – Y, факторный признак – X1.
Варианты 5-7: результативный признак – Y, факторный признак – X2.
Варианты 8-10: результативный признак – Y, факторный признак – X3.
Задание 2. На основании данных из таблицы П1 Приложения 1
§ Для переменных, соответствующих Вашему варианту (таблица 10.3), постройте корреляционную матрицу (в качестве первого списка переменных возьмите переменные Xi, в качестве второго списка – переменную Y).
§ Произведите графический анализ наиболее коррелированных переменных. Удалите случаи, негативно влияющие на коррелированность величин. Пересчитайте корреляционную матрицу. Сделайте вывод о том, как изменилась матрица после удаления данных.
§ Просмотрите корреляционную матрицу графически.
Таблица 10.3. Варианты заданий
| № варианта | Переменные | № варианта | Переменные |
| Y1, Y2, X4, X5 | Y2, Y3, X10, X11 | ||
| Y1, Y2, X6, X7 | Y2, Y3, X12, X13, | ||
| Y1, Y2, X8, X9 | Y2, Y3, X8, X9 | ||
| Y1, Y2, X10, X11 | Y1, Y3, X4,X5 | ||
| Y1, Y2, X12, X13 | Y1, Y3, X1, X4 |