Движение идеальной жидкости

21.1. Насосная станция города поддерживает в водопроводе на уровне первого этажа давление 5 атм. Определите (пренебрегая трением при течении жидкости) скорость струи воды, вытекающей из крана на первом, втором и третьем этажах, если краны каждого последующего этажа расположены на 4 м выше. На какой этаж вода по водопроводу уже не поднимется? [28,0; 27,3; 26,5 м/с. На двенадцатый этаж]

21.2. Сосуд с водой подвешен к потолку. Высота воды в сосуде h. На сколько изменится натяжение подвеса, если в днище сосуда открыть маленькое отверстие, из которого вытекает струя сечения S? Плотность воды r. [ ]

21.3. Насос должен подавать ежесекундно объем Q воды на высоту h по трубе постоянного сечения S. Какова должна быть мощность насоса? Плотность воды r. [ ]

 

21.4. а) Стационарный поток жидкости, протекающей по трубе переменного сечения, давит с силой F на участок A между сечениями 1и 2,который по третьему закону Ньютона давит с такой же силой в противоположном направлении. Следовательно, суммарная сила, действующая на жидкость со стороны этого участка, направлена против движения жидкости. Почему же жидкость в области 2имеет большую скорость, чем в области 1? [ а) Из-за разного давления в областях 1 и 2 на жидкость в области между 1 и 2 действует сила давления в направлении движения жидкости. Эта сила больше F ]

б) Чему равна суммарная сила, действующая на жидкость со стороны участка Л? Площади сечений в областях 1 и 2 равны S ₁и S ₂. Плотность жидкости r. В области 2 скорость жидкости равна v, давление равно нулю.[ б) ]

 

21.5. Из широкого сосуда через узкую цилиндрическую трубку вытекает жидкость плотности r. Как распределены по вертикали давление и скорость жидкости в сосуде и трубке? Давление воздуха Р _o. [В сосуде ; в трубке ]

 

21.6. По изогнутой под прямым углом трубе поперечного сечения S со скоростью v течет жидкость плотности r. С какой силой жидкость действует на трубу, если давление жидкости на выходе из трубы p? Силой тяжести пренебречь. [ ]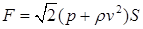

21.7. Насос представляет собой расположенный горизонтально цилиндр с поршнем площади S и выходным отверстием площади s, расположенным на оси цилиндра. Определите скорость истечения струи из насоса, если поршень под действием силы F перемещается с постоянной скоростью. Плотность жидкости r. [ ]

21.8. По наклонной плоскости стекает широкий поток воды. На расстоянии l по течению глубина потока уменьшилась вдвое. На каком расстоянии глубина потока уменьшится в 4 раза? [ x = 5 l ]

21.9. Плита массы т удерживается на месте в горизонтальном положении N струями жидкости, бьющими вертикально вверх из отверстий сечения S каждое. Скорость жидкости на выходе из отверстий v. На какой высоте над отверстиями удерживается плита? [ ]

21.10*. Во сколько раз увеличится сброс воды через широкую плотину, если уровень воды над кромкой плотины возрастет в 2 раза? Профиль плотины изображен на рисунке. [Размеры продольного сечения струи увеличатся в 2 раза. Скорости подобных участков в струе увеличиться в раза]

21.11*. Водосброс из широкого плоского сосуда происходит через треугольный вырез в его кромке. Во сколько раз уменьшится водосброс при понижении уровня воды от H до h? [Струи будут подобны. Размеры струи при понижении уровня воды уменьшатся в H / h раз, Поэтому выброс уменьшится в раз.]

21.12. Плоская бесконечная струя жидкости толщины h падает под углом a со скоростью v на плоскость. На какие струи распадается падающая струя? [На плоскости сохраняется энергия выделенных на рисунке участков струи и их суммарный импульс вдоль плоскости. Из закона сохранения энергии следует, что скорости этих участков на плоскости тоже будут равны v, а из закона сохранения импульса следует, что ]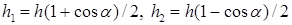

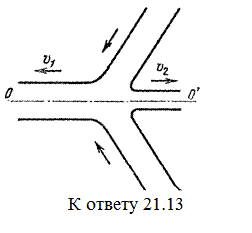21.13*. Две пластины, расположенные под углом 2a друг к другу, движутся со скоростью v по нормалям к своим поверхностям. Найдите скорости струй, возникающих при столкновении пластин, если движение материала пластин рассматривать как движение идеальной жидкости. [Нужно перейти в систему отсчета, в которой пластины движутся вдоль своих плоскостей. В этой системе материал пластин будет двигаться как две встречные струи, изображенные на рисунке. Их движение над и под плоскостью OO ^/ повторяет движение струи, рассмотренной в задаче выше: ]

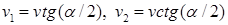21.14*. Определите форму стационарной струи после столкновения двух струй радиусов R и r, которые двигались навстречу друг другу с одинаковыми скоростями. [Конус с ]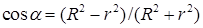

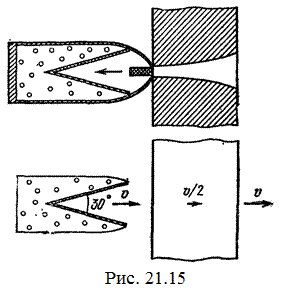21.15. «... В 1941 году немцы придумали кумулятивный противотанковый снаряд. На конусе снаряда – запал. При ударе он вызывает детонацию и воспламеняет весь заряд. Снаряд пробивает всю броню. В 1944 году такие немецкие снаряды попали в наши руки и руки союзников. Начался широкий эксперимент. При этом обнаружили много дополнительных эффектов и парадоксов. Стали выяснять – что же летит, что пробивает? Сперва думали, что этот снаряд бронепрожигающий, что броню пронзает струя горячего газа. Нет, оказалось, что летит металл...: перед плитой со скоростью 8 км/с, внутри плиты 4 км/с, за плитой снова 8 км/с»(Из вступительного слова председателя Президиума СО АН СССР академика М. А. Лаврентьева перед учащимися Летней физико-математической школы в 1971 году). Объясните это явление. Определите, с какой скоростью двигалась стенка металлической конической полости, перекрывающей заряд, если угол при вершине полости 30°. [Необходимо перейти в систему отсчета, в которой встречные скорости брони и струи металла будут равны по модулю. v_c = 1 км/с]

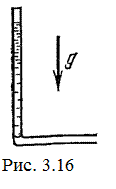
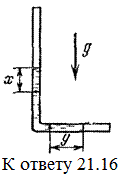
21.16*. Плотность жидкости r. В начальный момент она заполняет вертикальный участок длины l в тонкой L -образной трубке. Найдите, как зависит от времени высота уровня жидкости. Найдите распределение давления в момент, когда высота столба уменьшится наполовину. [ . в вертикальной части трубки, в горизонтальной части трубки (см. рис.)]

21.17*. Из отверстия в дне высокого сосуда вытекает вода. Сечение сосуда S,сечение струи s. Уровень воды сосуде перемещается с постоянным ускорением. Найдите это ускорение. [ ]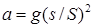

21.18. В цилиндре с поршнем находится вода, внутри которой в начальный момент имеется полость объема V. Поршень оказывает на воду постоянное давление p. Какую энергию приобретет вода в момент, когда полость исчезнет? [ ]

21.19*. Рассмотрите «замыкание» сферической полости в большом водоеме. Давление воды p,начальный радиус полости R. Определите скорость воды на границе полости в момент, когда ее радиус был равен r. [ ]

21.20. а) Оцените, при какой скорости кромки лопасти винта катера за лопастью возникнет полость. [При скорости, большей 14 м/с]

б *) При какой интенсивности ультразвука в воде при атмосферном давлении начнут появляться микрополости? Сжимаемость воды 5×10^–10 Па^–1. [При интенсивности, большей 700 Вт/м²]

 

 

Течение вязкой жидкости

22.1. Пространство между двумя параллельными плоскостями заполнено жидкостью вязкости h. Одна из плоскостей движется со скоростью v _o,другая покоится. Найдите распределение скоростей жидкости между плоскостями и силу вязкости, действующую на единицу площади каждой из плоскостей. Расстояние между плоскостями h. [ ]

22.2. Найдите распределение скоростей при установившемся течении жидкости между двумя плоскостями. Расстояние между плоскостями h,вязкость жидкости h. Найдите расход жидкости на единицу ширины потока, если перепад давления на единицу длины (в направлении движения жидкости) равен D p. [ 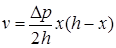, 0 < x < h; ]

22.3*. Жидкость перекачивается из одного сосуда в другой через длинную трубку радиуса R и длины l. Определите зависимость скорости жидкости от расстояния до стенки трубки, если разность давлений на концах трубки D p, вязкость жидкости h. [ ]

22.4. Определите расход жидкости на единицу ширины плоского потока, стекающего по наклонной плоскости под углом a к горизонту. Вязкость и плотность жидкости hи r. Толщина потока h. [ 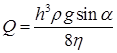]