Лабораторная работа № 10
Тема: Программирование задач аналитической геометрии.
Цель работы: освоить на практике методы разработки алгоритмов и их программной реализации при решении задачи с геометрическими объектами разного порядка.
Требования к выполнению работы
Для каждого из вариантов заданий необходимо составить алгоритм и программу, содержащую функции, которые предусматривают следующие действия:
- формирование элементов исходного множества случайным образом или вводом с клавиатуры;
- вывод исходных данных;
- обработка в соответствии с условием задачи;
- вывод результатов.
Теоретические сведения для выполнения работы
Основным геометрическим объектом, используемым в данных задачах, является множество точек на плоскости или в пространстве.
При программировании задач с геометрическими объектами могут быть использованы соотношения, действующие в метрическом пространстве Еn.
Множество материальных точек задается совокупностью координат.
Центр тяжести.множества материальных точек G:
G = (xi, yi, zi, mi), i=1, n (mi - масса i-й точки) имеет координаты:
x=  y=
y=  z=
z= 
Многоугольник (или n-угольник) - это замкнутая ломаная, состоящая из отрезков - сторон n-угольника. Многоугольник называется выпуклым, если для любой прямой, являющейся продолжением какой-нибудь стороны многоугольника, все другие его стороны находятся с одной и той же стороны от этой прямой. Центр тяжести выпуклого n-угольника:
x=  y=
y= 
Расстояние между двумя точками:
P1(x11,x12,…,x1n) и P2(x21,x22,…x2n):
L= 
Прямая, проходящая через две точки на плоскости Р1(х1,y1) и Р2(Х2,У2) описывается общим уравнением:
Ах + Ву + С = 0, где А = y2 – y1; В = х1 –х2; С = Ах1 – By1.
Прямая, проходящая через точку М перпендикулярно прямой Р1 - Р2, описывается уравнением –Bx + Ay + D = 0, где А, В определены выше, a
D = Dxm.- Aym,
Отклонение точки Р от прямой Ах + Ву + С = 0:
d = Axp + Byp + C,
если d<0, то точка Р находится справа от прямой; при d>0 - слева от прямой; при d = 0 - лежит на прямой (для прямой условно принимаем направление от точки P1 к точке Р2).
Расстояние R от точки Р до прямой Ax + By + C = 0.
R= 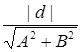
Координаты точки Р пересечения двух прямых
А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0
X  Y
Y  D=
D=  D
D  D
D 
Прямые параллельны, если D = 0; перпендикулярны, если скалярное произведение их направляющих векторов равно нулю, то есть
А1А2 + B1В2 = 0.
Площадь треугольника со сторонами a, b, c:
 , где
, где 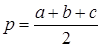
Три точки лежат на одной прямой, если S = 0.
Точка Р лежит внутри треугольника ABC, если она находится по одну сторону от прямых АВ, ВС и СА или если сумма площадей трех треугольников, образованых точкой Р и вершинами треугольника ABC равна площади треугольника ABC.
Треугольник с длинами сторон а, b и с {с= max(a, b, c)}:
- прямоугольный, если с2 = а2 + b2;
- остроугольный, если с2 < а2 + b2;
- тупоугольный, если с2 > а2 + b2:.
Уравнение плоскости, проходящей через три точки P1(x1, y1, z1), P2(x2, y2, z2) и P3(x3, y3, z3) имеет вид: Ах + Ву + Сz = 0, где
А = (у2 – у1)(z3 - z1) - (у3 – у1)(z2 - z3);
B = (x3 - x1)(z2 - z1) - (x2 - x1)(z3 - z1);
C = (x2 - x1)(y3 - y1) - (x3 - x1)(y2 - y1);
D = -(Ax1 + By1 + Cz1).
Плоскости перпендикулярны, если скалярное произведение нормалей
N1(А1, В1, С1) и N2(А2, В2, С2) равно нулю, то есть:
A1 A2 + B1 В2 + С1С2 = 0.
При решении задач следует учитывать приближенность представления вещественных чисел в ЭВМ. Это требует, чтобы при разработке алгоритма всюду, где производится сравнение вещественных значений, использовался некоторый задаваемый программистом уровень погрешности Е.
Варианты заданий.
Группа а
1. Задано множество М точек на плоскости. Найти две прямые, проходящие через две различные точки из М перпендикулярно соединяющему их отрезку и такие, чтобы внутри полосы, заключенной между этими прямыми, содержалось максимальное количество точек из М.
2. Из заданного множества точек на плоскости выбрать две различные точки так, чтобы количество точек, лежащих по разные стороны от прямой, проходящей через эти точки, различались наименьшим образом.
3. Определить радиус и центр окружности, на которой лежит наибольшее число точек заданного на плоскости множества точек.
4. Задано множество точек на плоскости. Выбрать из них три разные точки, которые являются вершинами треугольника наибольшего периметра.
5. Построить множество всех различных тупоугольных треугольников с вершинами в заданном множестве точек на плоскости.
6. Определить радиус и центр такой окружности, проходящей хотя бы через три различные точки заданного множества точек на плоскости, чтобы разность количества точек, лежащих внутри и вне окружности, была минимальной.
7. Даны два множества точек на плоскости. Указать центр и радиус окружности, проходящей через три точки первого множества и содержащего внутри себя наибольшее количество точек второго множества.
8. Построить множество всех различных остроугольных треугольников с вершинами в заданном множестве точек на плоскости и определить среди них треугольники максимальной и минимальной площади.
9. На плоскости задано множество окружностей. Список окружностей С(1), С{2),... С(n) называют цепочкой, если любые две смежные окружности C(i) и C(i+1) пресекаются. Выбрать в заданном множестве окружностей цепочку максимальной длины.
10. Расстояние между двумя множествами точек - это расстояние между наиболее близко расположенными точками этих множеств. Найти расстояние между двумя заданными множествами точек плоскости.
11. На плоскости заданы множество точек А и точка d вне его. Найти в А две такие точки а и b, чтобы треугольник abd имел максимальную площадь.
12. Найти такую точку заданного на плоскости множества точек, сумма расстояний от которой до остальных максимальна.
13. Задано множество точек М в трехмерном пространстве. Найти такую из них, чтобы шар заданного радиуса с центром в этой точке содержал максимальное число точек из М.
14. На плоскости заданы множество точек и окружность радиусом R с центром в начале координат. Найти остроугольный треугольник максимальной площади с вершинами в заданном множестве, расположенный строго внутри окружности.
15. Построить два треугольника с вершинами в заданном множестве точек на плоскости так, чтобы один из них лежал строго внутри другого, и разность их площадей была максимальной.
16 Задано множество прямых на плоскости коэффициентами своих уравнений. Подсчитать количество точек пересечений этих прямых и определить номер прямой, имеющий минимальное количество точек пересечения с другими прямыми.
l7. Из заданного множества точек на плоскости выбрать три разные точки А, В, С так, чтобы внутри треугольника ABC содержалось максимальное количество точек этого множества.
18. Задано множество прямых на плоскости коэффициентами своих уравнений. Определить номера прямых, точка пересечения которых расположена наиболее близко к началу координат.
19. В трехмерном пространстве задано множество материальных точек. Найти ту из них, которая наиболее близко расположена к центру тяжести этого множества.
20. В трехмерном пространстве задано множество материальных точек. Сгруппировать эти точки в порядке удаления их от центра тяжести этого множества.
21. В трехмерном пространстве задано множество материальных точек. Каждая из точек с максимальной массой исчезает, теряя десятую часть своей массы и раздавая оставшуюся массу поровну всем остальным, более "легким" точкам. Определить суммарную массу множества материальных точек в тот момент, когда все оставшиеся в нем точки имеют одинаковую массу (с определенной точностью).
22. Из данного на плоскости множества точек выбрать такие три точки, чтобы треугольник с вершинами в этих точках включал в себя все остальные точки заданного множества.
23. Определить радиус и центр окружности, проходящей, через три различные точки заданного множества точек на плоскости и не содержащей внутри себя других точек этого множества. Если таких окружностей несколько, выбрать из них окружность с максимальным радиусом.
24. На плоскости заданы множество точек А и точка D вне его. Подсчитать количество (неупорядоченных) различных троек точек а, b, с из А таких, что четырехугольник abсd является параллелограммом.
Группа б
1. На плоскости заданы множество точек А и множество окружностей В. Найти две такие различные точки из А, что проходящая через них прямая пересекается с максимальным количеством окружностей из В.
2. На плоскости заданы множество точек А и множество окружностей В. Найти две различные точки из А, что для проходящей через них прямой все непересекаемые ею окружности расположены от нее справа.
3. На плоскости задано множество окружностей. Выбрать среди них окружность, пересекающуюся с максимальным количеством других окружностей.
4. На плоскости заданы множество точек А и множество прямых В. Найти две такие различные точки из А, что проходящая через них прямая параллельна наибольшему количеству прямых из В.
5. На плоскости задано множество точек А и множество прямых В. Найти в множестве А такую точку, а в множестве B - такую прямую, чтобы расстояние между ними было минимальным.
6. На плоскости заданы множество точек А и точка d вне его. Определить количество прямых, проходящих через две различные точки множества А и точку d.
7. На плоскости заданы множество точек А и множество окружностей В. Найти две такие различные точки из А, что для проходящей через них прямой центры всех пересекаемых ею окружностей расположены от нее справа.
8. Определить радиус и центр окружности, проходящей, по крайней мере, через три различные точки заданного множества точек на плоскости и содержащей внутри наибольшее количество точек этого множества.
9. Из заданного множества точек на плоскости выбрать две различные точки таким образом, чтобы по отношению к прямой, проходящей через эти точки, максимальное количество остальных точек множества А располагалось справа от нее.
10. Даны два множества точек на плоскости. Из первого множества выбрать три различные точки так, чтобы треугольник с вершинами в этих точках содержал (строго внутри себя) максимальное количество точек второго множества.
11. Построить множество всех различных прямоугольных треугольников с вершинами в заданном множестве точек на плоскости и определить среди них треугольники с максимальной и минимальной площадью.
12. На плоскости заданы множество точек и окружность радиусом R с центром в начале координат. Через три точки заданного множества провести окружность максимального радиуса, полностью расположенную внутри заданной окружности.
13. Задано множество М точек на плоскости. Определить, сколько можно построить окружностей, проходящих через три произвольные точки множества М и не захватывающих других точек этого множества.
14. Даны два множества точек на плоскости. Выбрать три различные точки первого множества так, чтобы треугольник с вершинами в этих точках накрывал все точки второго множества и имел минимальную площадь.
15. Выбрать три различные точки из заданного множества точек на плоскости так, чтобы разность между количествами точек, лежащих внутри и вне треугольника с вершинами в выбранных точках, была минимальной.
16. Множество попарно различных плоскостей в трехмерном пространстве задано перечислением троек точек, через которые проходит каждая из плоскостей. Выбрать максимальное подмножество попарно непараллельных плоскостей.
17. Задано множество точек в трехмерном пространстве. Найти минимальный радиус шаров с центрами в этих точках, содержащих ровно n точек этого множества.
18. Выбрать три такие разные точки заданного на плоскости множества точек, которые составляют треугольник наибольшего периметра.
19. Из заданного на плоскости множества точек выбрать такие четыре точки, чтобы выпуклый четырехугольник с вершинами в этих точках включал в себя все остальные точки заданного множества.
20. На плоскости задано множество треугольников координатами своих вершин. Определить количество изолированных треугольников, то есть таких, которые не пересекаются с другими треугольниками и не находятся внутри других треугольников.
21. Задано множество точек на плоскости. Выбрать из них четыре разные точки, которые являются вершинами квадрата наибольшего периметра.
22. Из заданного множества точек на плоскости выбрать две различные точки так, чтобы окружности заданного радиуса с центрами в этих точках содержали внутри себя одинаковое количество точек.