Оглавление
Оглавление. 1
Вступление. 2
Биография Абрахам де Муавр. 3
Локальная теорема Муавра-Лапласа и формула Пуассона. 6
Список литературы.. 9
Вступление
Абрахам де Муавр внес значительный вклад в развитие аналитической тригонометрии и теории вероятностей. Есть легенда, согласно которой Муавр точно предсказал день собственной смерти: он обнаружил, что продолжительность его сна стала увеличиваться в арифметической прогрессии, и легко вычислил, когда она достигнет 24 часов, и, как всегда, не ошибся…
Биография Абрахам де Муавр
Родился 26 мая 1667 года во Франции в недворянской семье врача-гугенота; частицу де перед своей фамилией он добавил по собственной инициативе. В 11 лет поступил в Протестанскую академию в Седане, где успел проучиться 4 года, затем чего академия была запрещена властями (1682). Муавр продолжил образование в Сомюре (2 года). Вероятно, в это время он познакомился с теорией вероятностей по трудам Гюйгенса.
Далее примерно года Муавр слушал лекции по физике и математике в Париже, но в 1685 году Людовик XIV официально отменил Нантский эдикт, возобновились притеснения протестантов, а сам Муавр попал в тюрьму. Подробности его заключения неизвестны, но так или по-другому, он вынужден был оставить родину.
В 1688 году он осел в Лондоне, где и прожил всю оставшуюся бытие. На бытие зарабатывал частным преподаванием. Вскоре Муавр стал известен как одаренный математик, при всем при том как иноземец не имел никаких шансов на кафедру в английском учебном заведении. Религиозная дискриминация сменилась национальной.
Незадолго до его приезда вышла книжка Ньютона «Математические начала натуральной философии» в трёх томах. Она так увлекла Муавра, что он разобрал её по листам и стабильно носил с собой очередную порцию для чтения, чтобы не лишаться времени при переездах от одного ученика к другому.
1692: познакомился с Галлеем, а сквозь него — с Ньютоном. Вскоре они стали близкими друзьями. Ньютон отчаянно приподнято ценил Муавра. Если доверять сплетням той поры, Ньютон выпроваживал посетителей, досаждавших ему мелкими делами математического характера, с помощью следующей фразы: «Идите к де Муавру, он разбирается в этом лучше меня». Муавр ещё все время помогал Ньютону в издании и редактировании трудов (в особенности «Оптики»).
1695: опубликован первостепеннный работа Муавра по анализу, «Метод флюксий».
1697: Муавр избран членом Лондонского королевского общества.
1710: участвует в комиссии, разбиравшей приоритетный спор Ньютона с Лейбницем.
1718: публикует свой основной работа по теории вероятностей: «The Doctrine of Chance: A method of calculating the probabilities of events in play». Книга вызвала здоровенный заинтересованность и выдержала 3 издания.
1722: публикует формулу Муавра.
1724: вероятностно-статистическое изыскание «Annuities on lives» (переиздано четырежды).
1730: Муавр возвращается к анализу и публикует работа «Miscellanea Analytica», где впервой появляется формула Стирлинга.
По легенде, Муавр метко предсказал день собственной смерти. Обнаружив, что продолжительность его сна стала увеличиваться в арифметической прогрессии; он несложно вычислил, когда она достигнет 24 часов, и, как вечно, не ошибся.
Научная занятие
Муавр открыл (1707) формулу Муавра для возведения в уровень (и извлечения корней) комплексных чисел, заданных в тригонометрической форме.
Он основополагающий стал применять возведение в уровень бесконечных рядов.
Ему и Дж. Стирлингу принадлежит асимптотическое представление факториала, носящее наименование формулы Стирлинга.
Помимо анализа, Муавр внёс немалый вклад в теорию вероятностей. Доказал приватный случаи теоремы Лапласа. Провёл вероятностное изыскание азартных игр и ряда статистических данных по народонаселению. Кроме нормального, он использовал равномерное распределение. Для дискретного случая использовал и сильно исследовал последовательности, названные им рекуррентными (возвратными). Большинство результатов де Муавра были вскоре перекрыты трудами Лапласа; уровень возможного влияния де Муавра на Лапласа неясна.
Член Лондонского королевского общества (1697), Парижской (1754) и Берлинской (1735) академий.
Локальная теорема Муавра-Лапласа и формула Пуассона
Если вероятность наступления события А в каждом испытании постоянна, то вероятность того, что в n независимых испытаниях оно состоится т раз, при любом числе испытаний n определяется формулой Бернулли. Во всех рассмотренных примерах число испытаний было небольшим. Если же число испытаний велико, то вычисления искомых вероятностей по формуле Бернулли становятся очень громоздкими.
Например, если вероятность поражения мишени при одном выстреле равна 0,4, то вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, согласно формуле Бернулли можно получить формальный ответ. Но нахождение численного значения его даже с помощью таблиц логарифмов связано с серьезными трудностями. Кроме того, вычисления оказываются неточными, так как при сложении логарифмов, которые являются приближенными числами, ошибка накапливается. Поэтому, когда число испытаний велико, для нахождения вероятностей, нецелесообразно применять формулу Бернулли. Нужны формулы, по которым достаточно точные значения вероятностей находились бы при сравнительно несложных вычислениях. Поставленная задача имеет положительное решение. Такими формулами являются формулы Муавра — Лапласа и Пуассона,
Локальная теорема Муавра — Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз, приближенно равна:
.
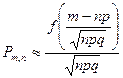где функция f(x) определяется равенством:
.
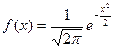Формула называется формулой Муавра — Лапласа. С возрастанием n относительная точность значений вероятностей, получаемых по ней, возрастает. В этом и заключается содержание локальной теоремы Муавра — Лапласа.
Для упрощения расчетов, связанных с применением формулы, составлена таблица значений функции f(x). Пользуясь этой таблицей, необходимо иметь в виду свойства функции, а именно:
1. Функция f(х) является четной, т. е. f (-х) = f (х). Поэтому в таблице приведены значения функции лишь для положительных значений аргумента.
2. Функция f(х) — монотонно убывающая при положительных значениях х. Предел f(х) при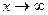 
равен нулю.
3. Если х > 5, то можно считать, что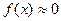 
. Функция f(х) уже при х = 5 очень мала: f(5) =0,0000015. Поэтому таблица значений функции f(х) не продолжена для значений х > 5.
Пример. Найти вероятность того, что при 600 выстрелах мишень будет поражена 250 раз, если вероятность поражения мишени при одном выстреле равна 0,4.
Решение. P=f(0.833)/12=0.0235.
Пример. Вероятность рождения мальчика равна 0,515. Найти вероятность того, что из 200 новорожденных будет 95 девочек.
Решение. Поскольку необходимо найти вероятность того, что будет 95 девочек, то в формулах через р должна обозначаться вероятность рождения девочки, при этом р = 1—0,515 == 0,485. При n = 200, р == 0,485 и q = 0,515 значение х, соответствующее m= 95, равно –0,283. По таблице находим, что f(0,283) = 0,3833. Поэтому окончательно имеем: P=0.3833/7.068=0.054.
Если вероятность р наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний т, но при небольшой величине произведения np, получаемые по формуле Муавра — Лапласа значения вероятностей оказываются недостаточно точными и возникает потребность в другой приближенной формуле для таких случаев.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна, но мала, число независимых испытаний n достаточно велико, но произведение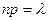 
остается небольшим, то вероятность 
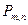того, что в этих испытаниях событие А наступит m раз,
.
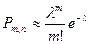Формула называется формулой Пуассона. Для упрощения расчетов, связанных с применением ее, составлена таблица значений функции Пуассона.
Пример. Пусть вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется пять нестандартных.
Решение. Здесь n = 1000, р = 0,004, а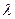 
= nр = 1000 • 0,004= 4. Все три числа удовлетворяют требованиям только что доказанной теоремы, а поэтому для нахождения вероятности искомого события применяем формулу Пуассона. По таблице значений функции Пуассона при 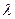=4 и m = 5 сразу получаем: P=0,1563.
Список литературы
1. https://newsland.com/news/detail/id/374931/?marketgid=pay
2. https://www.people.su/77122
3. https://ru.wikipedia.org/wiki/Муавр,_Абрахам_де
4. https://zfdasoa.ho.ua/matemat/text1.html
5. https://turboreferat.ru/statistics/vklad-uchenyh-v-raz..