Задача1.1.

| Масса груза и диска  , радиус диска , радиус диска  , жесткость пружин , жесткость пружин  . Длины пружин в ненапряжённом состоянии . Длины пружин в ненапряжённом состоянии  . Считать, что расстояние между крайними точками крепления пружин . Считать, что расстояние между крайними точками крепления пружин  .
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний.
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать абсолютные координаты .
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний.
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать абсолютные координаты  груза и центра масс диска. груза и центра масс диска.
|
Решение.
1. Уравнения малых колебаний.
Если пренебречь размерами груза, то текущие длины пружин (слева направо)  .
.
Их удлинения:  .
.
Потенциальная энергия пружин
 .
.
В положении равновесия первые производные равны нулю, уравнения равновесия
 ,
,
Решение уравнений равновесия определяет значения обобщённых координат в положении равновесия
 .
.
Вторые производные потенциальной энергии в положении равновесия
 .
.
Матрица жесткостей, равная  , положительно определена.
, положительно определена.
Кинетическая энергия  .
.
Матрица инерции для вектора переменных  равна
равна 
Уравнения малых колебаний для отклонений от положения равновесия 

В матричной форме  , или
, или  , где матрица системы
, где матрица системы
 ,
,  - оператор дифференцирования по времени.
- оператор дифференцирования по времени.
2. Решение уравнений малых колебаний.
Характеристическое уравнение
 .
.
Корни характеристического уравнения
 .
.
Замечание 1: в случае устойчивой консервативной системы, когда матрица жесткостей положительно определена, следует записывать частотное уравнение
 .
.
Решение частотного уравнения определяет собственные частоты колебаний
 .
.
Общее решение уравнений малых (линейных) собственных колебаний устойчивой консервативной системы с двумя степенями свободы имеет вид
 ,
,
Для определения модальных столбцов  запишем матрицу
запишем матрицу  , присоединённую к матрице системы
, присоединённую к матрице системы 
 .
.
Подставляя в присоединённую матрицу значения собственных частот  , получим
, получим
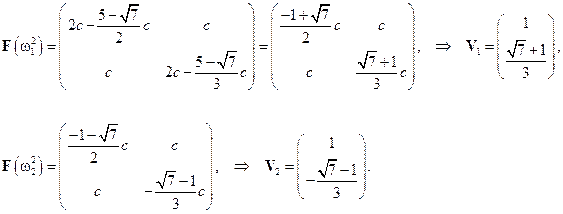
Замечание 2:
Обратите внимание на то, что модальные столбцы записаны без постоянного для всех элемента множителя  . Это упрощает дальнейшие выкладки.
. Это упрощает дальнейшие выкладки.
Замечание 3:
Знаки элементов модального столбца  одинаковы, что свидетельствует о том, что колебания с первой, меньшей частотой – синфазные, противоположные знаки элементов модального столбца
одинаковы, что свидетельствует о том, что колебания с первой, меньшей частотой – синфазные, противоположные знаки элементов модального столбца  говорят о том, что колебания со второй частотой происходят в противофазе.
говорят о том, что колебания со второй частотой происходят в противофазе.
Окончательно, решение уравнений будет

Константы  имеют размерность метра.
имеют размерность метра.
3. Гармонические коэффициенты влияния.
Модальная матрица системы (матрица, составленная из модальных столбцов)
 .
.
Обратите внимание на то, что эта матрица не особая, 
Приведённые массы  положительны
положительны

Нормированная модальная матрица
 .
.
В соответствии с данной на лекции формулой 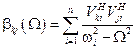 , где
, где  элементы
элементы  -го столбца
-го столбца  -ой и
-ой и  -ой строк соответственно, гармонические коэффициенты влияния равны
-ой строк соответственно, гармонические коэффициенты влияния равны

Коэффициент  равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по первой же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к грузу приложена сила
равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по первой же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к грузу приложена сила  , а
, а  .
.
Амплитуда вынужденных колебаний по первой обобщённой координате при возмущении по первой обобщённой координате, согласно лекционному материалу, равна 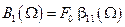 . Размерность
. Размерность  равна
равна 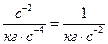 , при умножении на ньютон получим метр, что отвечает размерности амплитуды обобщённой координаты
, при умножении на ньютон получим метр, что отвечает размерности амплитуды обобщённой координаты  .
.
Если частота возмущения  равна
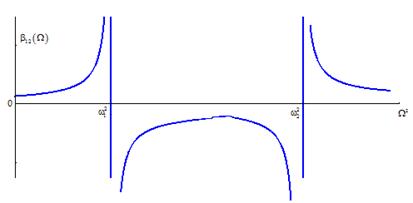
равна  , амплитуда вынужденных колебаний по первой обобщённой координате равна нулю. Несложно убедиться в том, что частота антирезонанса лежит между собственными частотами.
, амплитуда вынужденных колебаний по первой обобщённой координате равна нулю. Несложно убедиться в том, что частота антирезонанса лежит между собственными частотами.

Коэффициент  равен с точностью до множителя амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по второй же обобщённой координате и амплитуда гармонического возмущения равна 1. Если частота возмущения
равен с точностью до множителя амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по второй же обобщённой координате и амплитуда гармонического возмущения равна 1. Если частота возмущения  равна
равна  , амплитуда вынужденных колебаний по второй обобщённой координате равна нулю.
, амплитуда вынужденных колебаний по второй обобщённой координате равна нулю.

Коэффициент  равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по второй обобщённой координате и амплитуда гармонического возмущения равна 1. Или наоборот: амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по первой обобщённой координате. Антирезонансные частоты отсутствуют.
равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по второй обобщённой координате и амплитуда гармонического возмущения равна 1. Или наоборот: амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по первой обобщённой координате. Антирезонансные частоты отсутствуют.
Ниже приведены характерные графики 

Задача 1.2. (отличается от предыдущей задачи выбором обобщённых координат)

| Масса груза и диска  , радиус диска , радиус диска  , жесткость пружин , жесткость пружин  . Длины пружин в ненапряжённом состоянии . Длины пружин в ненапряжённом состоянии  . Считать, что расстояние между крайними точками крепления пружин . Считать, что расстояние между крайними точками крепления пружин  , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать  - координату груза, - координату груза,  - угол поворота диска (против часовой стрелки). Считать, что при напряжённых пружинах угол - угол поворота диска (против часовой стрелки). Считать, что при напряжённых пружинах угол  равен нулю. равен нулю.
|
Решение.
1. Уравнения малых колебаний.
Удлинения пружин (слева направо):  .
.
Потенциальная энергия пружин
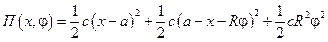 .
.
В положении равновесия первые производные  равны нулю, уравнения равновесия
равны нулю, уравнения равновесия
 ,
,
Решение уравнений равновесия определяет значения обобщённых координат в положении равновесия
 .
.
Вторые производные потенциальной энергии в положении равновесия
 .
.
Матрица жесткостей, равная
 ,
,
положительно определена.
Кинетическая энергия  .
.
Матрица инерции для вектора переменных 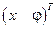 :
: 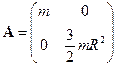 .
.
Уравнения малых колебаний для отклонений от положения равновесия 

Или в матричной форме  , или
, или 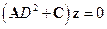 , где матрица системы
, где матрица системы
 ,
,  - оператор дифференцирования по времени.
- оператор дифференцирования по времени.
2. Решение уравнений малых колебаний.
Частотное уравнение
 .
.
Решение частотного уравнения определяет собственные частоты колебаний
 .
.
Для определения модальных столбцов  запишем матрицу
запишем матрицу  , присоединённую к матрице системы
, присоединённую к матрице системы 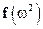
 .
.
Подставляя в присоединённую матрицу значения собственных частот  , получим
, получим

Замечание 4:
Обратите внимание, что элементы модальных столбцов имеют разную размерность. И это естественно, так как первая координата линейная, а вторая угловая, и размерности элементов модальных столбцов вполне этому соответствуют.
Замечание 5:
Знаки элементов модального столбца 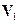 противоположны, что свидетельствует о том, что колебания с первой, меньшей частотой при таком выборе обобщённых координат – противофазные, одинаковые знаки элементов модального столбца
противоположны, что свидетельствует о том, что колебания с первой, меньшей частотой при таком выборе обобщённых координат – противофазные, одинаковые знаки элементов модального столбца  говорят о том, что колебания со второй частотой – синфазные.
говорят о том, что колебания со второй частотой – синфазные.
Решение уравнений имеет вид
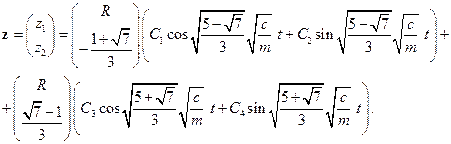
Константы  безразмерные.
безразмерные.
3. Гармонические коэффициенты влияния.
Модальная матрица системы (матрица, составленная из модальных столбцов)
 .
.
Приведённые массы  положительны
положительны

Нормированная модальная матрица
 .
.
В соответствии с данной на лекции формулой  , где
, где  элементы
элементы  -го столбца
-го столбца  -ой и
-ой и  -ой строк соответственно, гармонические коэффициенты влияния равны
-ой строк соответственно, гармонические коэффициенты влияния равны

Коэффициент  равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по первой же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к грузу приложена сила
равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по первой же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к грузу приложена сила  , а
, а  .
.
Амплитуда вынужденных колебаний по первой обобщённой координате при возмущении по первой обобщённой координате, согласно лекционному материалу, равна  . Размерность
. Размерность  равна
равна 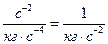 , при умножении на ньютон получим метр, что отвечает размерности амплитуды обобщённой координаты
, при умножении на ньютон получим метр, что отвечает размерности амплитуды обобщённой координаты  .
.
Если частота возмущения  равна
равна  , амплитуда вынужденных колебаний по первой обобщённой координате равна нулю. Несложно убедиться в том, что частота антирезонанса лежит между собственными частотами.
, амплитуда вынужденных колебаний по первой обобщённой координате равна нулю. Несложно убедиться в том, что частота антирезонанса лежит между собственными частотами.
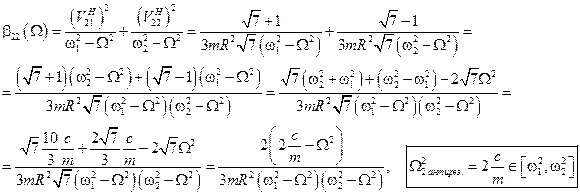
Коэффициент  равен с точностью до множителя амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по второй же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к диску приложен момент
равен с точностью до множителя амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по второй же обобщённой координате и амплитуда гармонического возмущения равна 1. В данной задаче это означает, что к диску приложен момент  , а
, а  .
.
Амплитуда вынужденных колебаний по второй обобщённой координате при возмущении по второй обобщённой координате, согласно лекционному материалу, равна  . Размерность
. Размерность  равна
равна  , при умножении на
, при умножении на  , получим безразмерную величину, что отвечает размерности амплитуды обобщённой координаты
, получим безразмерную величину, что отвечает размерности амплитуды обобщённой координаты  .
.
Если частота возмущения  равна
равна  , амплитуда вынужденных колебаний по второй обобщённой координате равна нулю.
, амплитуда вынужденных колебаний по второй обобщённой координате равна нулю.
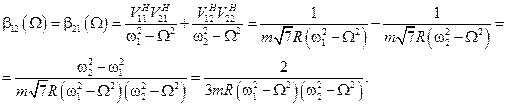
Коэффициент  равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по второй обобщённой координате и амплитуда гармонического возмущения равна 1. Или наоборот: амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по первой обобщённой координате. Антирезонансные частоты отсутствуют.
равен с точностью до множителя амплитуде колебаний по первой обобщённой координате, если возбуждение происходит по второй обобщённой координате и амплитуда гармонического возмущения равна 1. Или наоборот: амплитуде колебаний по второй обобщённой координате, если возбуждение происходит по первой обобщённой координате. Антирезонансные частоты отсутствуют.
Если к диску приложен момент  ,
,  , то амплитуда вынужденных колебаний по первой обобщенной координате (амплитуда колебаний груза) равна
, то амплитуда вынужденных колебаний по первой обобщенной координате (амплитуда колебаний груза) равна  . Размерность
. Размерность  равна
равна 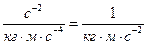 , при умножении на
, при умножении на  , получим величину, имеющую размерность метра, что отвечает размерности амплитуды обобщённой координаты
, получим величину, имеющую размерность метра, что отвечает размерности амплитуды обобщённой координаты  .
.
Задача 2. (неустойчивая консервативная система)
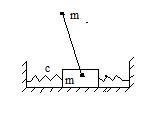
| Рассматриваются колебания около вертикали перевёрнутого маятника с подвижной точкой подвеса. Масса груза и точечной массы на конце невесомого стержня длины  равны равны  , жесткость пружин , жесткость пружин  . Длины пружин в ненапряжённом состоянии . Длины пружин в ненапряжённом состоянии  . Считать, что расстояние между крайними точками крепления пружин . Считать, что расстояние между крайними точками крепления пружин  , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
В качестве обобщённых координат выбрать , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
В качестве обобщённых координат выбрать  - координату груза, - координату груза, 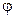 - угол отклонения маятника (против часовой стрелки). - угол отклонения маятника (против часовой стрелки).
|
Решение.
1. Уравнения малых колебаний.
Удлинения пружин (слева направо): 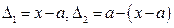 .
.
Потенциальная энергия пружин  . Потенциальная энергия силы тяжести
. Потенциальная энергия силы тяжести  . Итого
. Итого 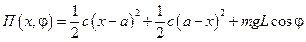 .
.
В положении равновесия первые производные  равны нулю, уравнения равновесия
равны нулю, уравнения равновесия
 ,
,
Верхнему положению равновесия соответствуют значения обобщённых координат
 .
.
Вторые производные потенциальной энергии в положении равновесия
 .
.
Матрица жесткостей, равная
 ,
,
не является положительно определенной.
Кинетическая энергия системы равна  , где
, где  квадрат скорости точечной массы, причем
квадрат скорости точечной массы, причем

Тогда кинетическая энергия  .
.
Матрица инерции (переменная) для вектора переменных  :
:
 .
.
Для составления линейных уравнений берём матрицу инерции  в положении равновесия
в положении равновесия
 .
.
Уравнения малых колебаний для отклонений от положения равновесия 

Или в матричной форме  , или
, или  , где матрица системы
, где матрица системы
 .
.
2. Решение уравнений малых колебаний.
Характеристическое уравнение
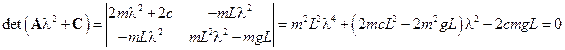 .
.
Или

Квадраты корней характеристического уравнения, как и следовало ожидать, действительны и имеют различные знаки
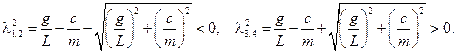 .
.
Значит, имеем пару мнимых корней и пару действительных противоположных знаков

В данном случае общее решение уравнений малых (линейных) собственных колебаний имеет вид
 ,
,
Для определения модальных столбцов  запишем матрицу
запишем матрицу  , присоединённую к матрице системы
, присоединённую к матрице системы 
 .
.
Подставляя в присоединённую матрицу значения квадратов корней характеристического уравнения  , получим
, получим


Например, если допустить, что  , то квадраты корней характеристического уравнения и модальные столбцы будут
, то квадраты корней характеристического уравнения и модальные столбцы будут

Общее решение уравнений имеет вид

Константы  безразмерные.
безразмерные.
2. Домашнее задание
Задача.

| Масса груза и диска  , радиус диска , радиус диска  , жесткость пружин , жесткость пружин  . Длины пружин в ненапряжённом состоянии . Длины пружин в ненапряжённом состоянии  . Считать, что расстояние между крайними точками крепления пружин . Считать, что расстояние между крайними точками крепления пружин  , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать абсолютную координату груза , размерами груза пренебречь.
1. Составить уравнения малых колебаний системы около положения равновесия.
2. Записать решение уравнений колебаний
3. Найти коэффициенты гармонического влияния.
В качестве обобщённых координат выбрать абсолютную координату груза  и относительную координату и относительную координату  центра диска. центра диска.
|
3. Исправление результатов тестирования. Для тех, кто писал тест.
В этих задачах составить инерционную матрицу и матрицу жесткостей. Построить решение системы. Результаты выслать. Я выбрала работы, в которых было допущено много ошибок и двойки, конечно.
ВАРИАНТ 1 Клинков
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Моменты инерции дисков  ; крутильные жесткости валов ; крутильные жесткости валов  .
В качестве обобщенных координат выбрать абсолютные углы .
В качестве обобщенных координат выбрать абсолютные углы 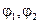 поворота дисков. Угловая скорость второго диска поворота дисков. Угловая скорость второго диска  . .

|
ВАРИАНТ 2 Дай Цяо
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Моменты инерции  , крутильные жесткости валов , крутильные жесткости валов  .
В качестве обобщенных координат выбрать угол .
В качестве обобщенных координат выбрать угол  поворота первого диска и угол поворота поворота первого диска и угол поворота  второго диска относительно первого. второго диска относительно первого.

|
ВАРИАНТ 3 Гриневич
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Массы грузов  и и  ; жесткости пружин ; жесткости пружин  .
В качестве обобщенных координат выбрать абсолютные координаты .
В качестве обобщенных координат выбрать абсолютные координаты  грузов. грузов.
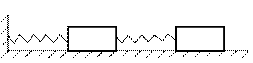
|
ВАРИАНТ 4 Зацепин
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
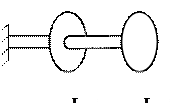
Моменты инерции дисков: первый  , второй , второй  ; крутильные жесткости валов ; крутильные жесткости валов  .
В качестве обобщенных координат выбрать абсолютные углы .
В качестве обобщенных координат выбрать абсолютные углы 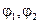 поворота дисков. поворота дисков.
|
ВАРИАНТ 5 Беленов
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Массы грузов  , жесткости пружин , жесткости пружин  .
В качестве обобщенных координат выбрать координату .
В качестве обобщенных координат выбрать координату  первого груза и координату первого груза и координату  второго груза относительно первого. Скорость второго груза второго груза относительно первого. Скорость второго груза 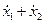

|
ВАРИАНТ 6 Камаламба
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Моменты инерции дисков: первый  , второй , второй  ; крутильные жесткости валов ; крутильные жесткости валов  .
В качестве обобщенных координат выбрать угол .
В качестве обобщенных координат выбрать угол  поворота первого диска и угол поворота поворота первого диска и угол поворота  второго диска относительно первого. второго диска относительно первого.

|
ВАРИАНТ 8 Нэту
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Массы грузов  , жесткости пружин , жесткости пружин  .
В качестве обобщенных координат выбрать абсолютные координаты .
В качестве обобщенных координат выбрать абсолютные координаты  грузов. грузов.

|
ВАРИАНТ 9 НевскийДопущены ошибки при решении частотного уравнения
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Массы диска и груза  , радиус диска , радиус диска  , жесткости пружин , жесткости пружин  .
В качестве обобщенных координат выбрать координату .
В качестве обобщенных координат выбрать координату  груза и координату груза и координату 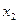 центра диска относительно груза. центра диска относительно груза.

|
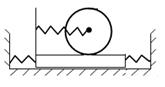
ВАРИАНТ 10 Шаграй
Составить инерционную матрицу и матрицу жесткостей. Найти собственные частоты.
Массы диска и груза  , радиус диска , радиус диска  , жесткости пружин , жесткости пружин  .
В качестве обобщенных координат выбрать координату .
В качестве обобщенных координат выбрать координату  груза и угол груза и угол  поворота диска. поворота диска.
|
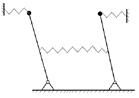
ВАРИАНТ 11 Лущенко
Составить инерционную матрицу и матрицу жесткостей. Определить условие устойчивости положения равновесия. Найти собственные частоты.
Стержни невесомые длины  , точечные массы на концах стержней , точечные массы на концах стержней  , жесткости пружин , жесткости пружин  .
В положении равновесия маятники занимают вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать углы .
В положении равновесия маятники занимают вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать углы  отклонения маятников. отклонения маятников.
|
ВАРИАНТ 12 Шестаков
Составить инерционную матрицу и матрицу жесткостей. Определить условие устойчивости положения равновесия. Найти собственные частоты.
Стержни невесомые длины  , точечные массы на концах стержней , точечные массы на концах стержней  , жесткости пружин , жесткости пружин  .
В положении равновесия маятники занимают вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать углы .
В положении равновесия маятники занимают вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать углы  отклонения маятников. отклонения маятников.

|
ВАРИАНТ 13 Малышев
Составить инерционную матрицу и матрицу жесткостей. Определить условие устойчивости положения равновесия. Найти собственные частоты.
Стержень невесомый длины  , масса груза и точечной массы на конце стержня , масса груза и точечной массы на конце стержня 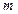 , жесткости пружин , жесткости пружин  . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату  груза и угол груза и угол  отклонения маятника. отклонения маятника.

|
ВАРИАНТ 15 Носенко
Составить инерционную матрицу и матрицу жесткостей. Определить условие устойчивости положения равновесия. Найти собственные частоты.
Стержень невесомый длины  , масса груза и точечной массы на конце стержня , масса груза и точечной массы на конце стержня 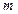 , жесткости пружин , жесткости пружин  . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату  груза и угол груза и угол  отклонения маятника. отклонения маятника.

|
ВАРИАНТ 17 Назаркин
Составить инерционную матрицу и матрицу жесткостей. Определить условие устойчивости положения равновесия. Найти собственные частоты.
Стержень невесомый длины  , масса груза и точечной массы на конце стержня , масса груза и точечной массы на конце стержня 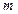 , жесткости пружин , жесткости пружин  . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату . В положении равновесия маятник занимает вертикальное положение, пружины не напряжены.
В качестве обобщенных координат выбрать координату  груза и угол груза и угол  отклонения маятника. отклонения маятника.

|