ТЕМА 4. Основы корреляционного анализа
Вопросы:
1. Функциональные и стохастические типы связей.
2. Корреляционный анализ:
2.1. Парная корреляция.
2.2. Множественная корреляция.
2.3. Частная корреляция.
3. Пример корреляционного анализа трех переменных.
Функциональные и стохастические типы связей
Большинство явлений и процессов в экономике находятся в постоянной взаимной и всеохватывающей объективной связи. Для исследования этих зависимостей широко применяется аппарат корреляционно-регрессионного анализа. Он используется при решении задач анализа, планирования и прогнозирования хозяйственной деятельности.
Различают два вида зависимостей между экономическими переменными:
1) функциональная;
2) стохастическая (вероятностная, статистическая).
При функциональной связи по значению одной переменной (экзогенной) можно найти вполне определенное значение другой (эндогенной). Такие связи между реальными экономическими переменными встречаются редко. В большинстве случаев экономические переменные подвержены действию различных случайных факторов. Тогда по значению одной из них можно лишь предсказать с определенной вероятностью или найти среднее значение другой. Такие связи называют стохастическими (вероятностными, статистическими). Иногда их называют корреляционными. В этом случае о связи переменных можно говорить лишь в вероятностном смысле.
Корреляционный анализ
Корреляционный анализ предназначендля выявления и оценки количественных взаимосвязей экономических переменных на основе коэффициентов корреляции.
Виды корреляции:
1) по направлению связей:
- положительная,
- отрицательная;
|
|
2) по форме связи переменных:
- линейная,
- нелинейная;
3) по числу переменных:
- парная,
- множественная,
- частная.
Задачи корреляционного анализа:
1) оценка тесноты связи переменных;
2) определение направления связи переменных;
3) выбор ведущих (информативных) факторов для исследуемой переменной;
4) выявление ранее неизвестных причинных связей.
Для решения этих задач используют три основных вида коэффициентов корреляции:
1) парные,
2) множественные,
3) частные.
Парная корреляция
Выборочный коэффициент парной линейной корреляции позволяет оценить силу и направление связи между двумя линейно зависящими друг от друга переменными.
,
где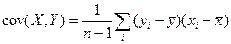 
– ковариация случайных переменных X и Y; 
, 
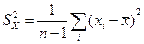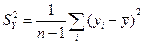– дисперсии (вариации) случайных переменных X и Y [1].
Замечания:
1. Ковариация случайных переменных x и y – это величина, определяемая по формуле 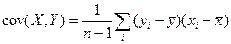и позволяющая оценивать силу и направление связи двух переменных. Геометрическая интерпретация: ковариация характеризует степень рассеяния точек с координатами 
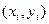вокруг точки 
(рис.1).
Рис.1. Ковариация переменных X и Y.
Силу и направление связи двух переменных определяют и коэффициенты парной корреляции. Они являются безразмерными величинами. Ковариация же измеряется в определенных единицах. Этим обусловлено неудобство ее практического использования.
2. Дисперсия (вариация) случайной переменной Y – это степень отклонения ее значений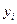 
от среднего 
(рис. 2), которая определяется по формуле
.
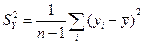Рис. 2. Дисперсия (вариация) случайной переменной Y
Свойства коэффициента парной корреляции:
|
|
1) 
;
2) если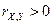 
, то связь между переменными x и y прямая (с ростом одной переменной растет и другая и наоборот);
3) если 
, то связь между переменными x и y обратная (с ростом одной переменной другая уменьшается и наоборот);
4) если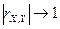 
, то связь между переменными тесная (сильная); при 
корреляционная связь представляется линейной функциональной зависимостью;
5) если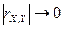 
, то связь между переменными слабая; при 
связь отсутствует.
Коэффициент парной корреляции называется выборочным, так как рассчитывается по некоторой выборочной совокупности данных (выборке). Возможность перенесения полученных результатов на генеральную совокупность дает статистическая значимость выборочного коэффициента парной корреляции. Проверка статистической значимости коэффициента осуществляется на основе t -критерия Стьюдента:
.
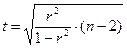Если 
, то коэффициент парной корреляции признается значимым.
Замечание:
Для определения 
можно использовать статистическую функцию в Excel СТЬЮДРАСПОБР, предварительно задав два параметра 
. Параметр 
определяет уровень вероятности Р расчетов и связан с ней формулой
.
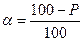Второй параметр (n-2) называется числом степеней свободы [2], то есть числом степеней свободы независимого варьирования признака. Это число связано с числом единиц совокупности n и с числом определяемых по ней констант в уравнении регрессии (для случая двух переменных в уравнении будут определяться два параметра).
Предположим, что имеется не две, а совокупность переменных 
. Тогда для каждой пары переменных можно определить коэффициент парной корреляции. Все вместе они образуют матрицу коэффициентов парной корреляции или корреляционную матрицу КМ
|
|
.
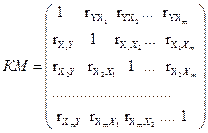Очевидно, что матрица КМ может быть записана в треугольном виде, так как два ее треугольника одинаковы
Основным назначением корреляционной матрицы является выбор ведущих (информативных) факторов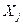 
для исследуемой переменной Y. Для выбора ведущих факторов поступают следующим образом:
1. В первом столбце матрицы R находят коэффициенты, у которых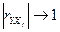 
. Это означает, что соответствующие им факторы 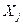имеют тесную связь с исследуемой переменной Y.
2. Оценивают статистическую значимость выбранных коэффициентов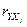 
по t-критерию Стьюдента.
3. Отобранные факторы проверяют на наличие между ними тесной связи (коллинеарности или мультиколлинеарности).
Два фактора 
называются коллинеарными, если 
. Иными словами, коллинеарные факторы – это факторы, тесно связанные между собой.
Тесную связь более чем двух факторов называют мультиколлинеарностью. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами (матрица межфакторных корреляций)
.
Чем ближе он к нулю, тем сильнее мультиколлинеарность факторов и ненадежнее результаты регрессионного анализа (см. тему 2, 3). И наоборот, чем ближе к единице определитель матрицы межфакторных корреляций, тем меньше мультиколлинеарность факторов.
На практике для построения корреляционных матриц можно использовать инструмент «Корреляция» из пакета «Анализ данных» в Excel (показать примеры построения и анализа корреляционных матриц, используя данные из файла «Примеры - корреляция и регрессия»).
Множественная корреляция
Для оценки тесноты связи одной случайной величины с совокупностью других величин используется коэффициент множественной корреляции.
Пусть имеется совокупность переменных . Выборочный коэффициент множественной корреляции переменной Y с факторами 
рассчитывается по формуле
,
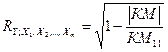где 
– определитель корреляционной матрицы КМ; 
– алгебраическое дополнение к элементу 
корреляционной матрицы, стоящему на пересечении первого столбца и первой строки, которым соответствует расположение элемента Y.
Свойства коэффициента R:
1) 
,
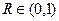2) если 
, то переменные в совокупности сильно влияют на переменную Y,
3) коэффициент R не позволяет анализировать направления связей.
Частная корреляция
Если рассматривать несколько коррелирующих друг с другом случайных переменных, то на величине коэффициентов парной корреляции частично сказывается влияние других величин. В частности, соответствующие коэффициенты корреляции могут быть неоправданно завышены. Поэтому возникает необходимость исследования частной корреляции между переменными, которая оценивается при фиксировании или исключении влияния других переменных.
Рассмотрим случай трех переменных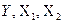 
. В формулах для расчета частных коэффициентов корреляции используются только коэффициенты парной корреляции из корреляционной матрицы:
а) частная корреляция Y c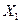 
при фиксировании влияния фактора 
;
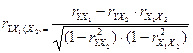б) частная корреляция Y c при фиксировании влияния фактора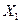
.
Свойства частных коэффициентов корреляции аналогичны свойствам коэффициентов парной корреляции.