Механика жидкостей
В жидкостях межатомные расстояния неизменны и поэтому жидкость обладает неизменным объемом.
Жидкость принимает форму того сосуда, в который она заключена.
В механике жидкости рассматривают как сплошные, непрерывно распределенные в занятой ими части пространства.
Несжимаемая жидкость - это жидкость, плотность которой всюду одинакова и не изменяется со временем.
Давление в жидкости
Если в покоящуюся жидкость поместить пластинку площадью S, то на нее действует сила 
, которая направлена перпендикулярно плоскости пластины и величина 
называется давлением жидкости, измеряется в паскалях [Па], 1 Па = 1 Н/м2.
Закон Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям и передается по всему объему, занятому покоящейся жидкостью.
Гидростатическое давление – это давлениестолба жидкости высотой h и поперечным сечением S на нижнее основание столба: P =ρgh, здесь r - плотность жидкости.
Закон Архимеда. Поскольку сила давления на нижние слои жидкости больше, чем на верхние, то поэтому на тело, погруженное в жидкость, действует сила, направленная вверх, выталкивающая тело, равная весу вытесненной телом жидкости: FA = ρg υ, где υ - объем погруженного в жидкость тела.
Уравнение неразрывности
Движение жидкостей называется течением.
Совокупность частиц движущейся жидкости называется потоком.
Линия тока - это линия, проведенная так, что касательная к ней совпадает по направлению с вектором скорости жидкости в соответствующих точках пространства (см.рис.1).
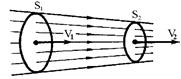
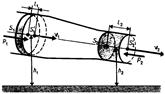
Рис. 1. Рис. 2. Рис. 3. Рис. 4.
Часть жидкости, ограниченная линиями тока, называется трубкой тока (см. рисунок).
Течение жидкости называют стационарным (установившимся), если форма и расположение линий тока, а также скорости в каждой точке жидкости, со временем не изменяются.
Течение жидкости называют стационарным, если скорость движения жидкости, со временем не изменяется.
Для стационарного течения жидкости справедливо уравнение неразрывности (см. рис. 2):
S 1 V 1 = S 2 V 2 = const, (*)
где S 1, S 2 - сечения трубки, по которой течет жидкость,
V 1, V 2 - скорости течения жидкости в месте сечений S 1 и S 2,
физический смысл произведения SV - объем жидкости, проходящей через сечение S за 1 с.
Уравнение Бернулли
При стационарном течении жидкости для любого сечения трубки тока справедливо уравнение Бернулли (см. рис. 3):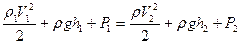 
или 
,
для горизонтальной трубки 
, (**)
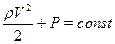где r - плотность жидкости, V - скорость течения в месте выбранного сечения, g - ускорение свободного падения, h - высота, на которой располагается выбранное сечение, P - давление в месте выбранного сечения (давление жидкости на поверхность обтекаемого ею тела, см. рис. 3).
Принятая терминология: Р – статистическое давление,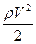 
- динамическое давление, rgh – гидростатическое давление, 
– полное давление.
Уравнение Бернулли есть выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости: при выводе уравнения Бернулли рассматривается перемещение жидкости от сечения S1 (
) до сечения S2 (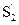
), причем считается, что расстояния ℓ1 и ℓ2 настолько малы, что все точки жидкости в объемах между сечениями S1 (S2) и (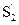) имеют постоянные значения скорости, давления и высоты.
Уравнение Бернулли хорошо применимо и для реальных жидкостей, внутреннее трение которых не очень велико.
Из уравнений (*) и (**) следует, что при течение жидкости по горизонтальной трубке, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах: в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.
Уравнение Бернулли используется для измерения скорости потока жидкости (экспериментально измеряется динамическое давление).
Вязкость жидкости. Ламинарный и турбулентный режимы течения.
Вязкость (внутреннее трение) - это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.
При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев (рис. 4).
Модуль силы внутреннего трения: 
, где D x - расстояние между двумя соседними слоями, D V - разность скоростей жидкости в двух соседних слоях,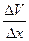 
- градиент скорости, S - площадь соприкосновения двух соседних слоев, h - коэффициент вязкости, зависящий от природы жидкости и температуры.
Единица вязкости - паскаль-секунда [Па.с]: 1 Па.с равен вязкости среды, в которой при градиенте скорости с модулем 1м/с, возникает сила внутреннего трения 1 Н на 1 м2 поверхности касания слоев (1 Па.с = 1 Н.с/м2).
Ламинарное (слоистое) течение жидкости - когда вдоль потока каждый выделенный слой скользит относительно соседних, не перемешиваясь с ними. Этот режим наблюдается при небольших скоростях движения жидкости.
Турбулентное (вихревое) течение жидкости - когда вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости. При этом режиме течения частицы жидкости приобретают составляющие скоростей, перпендикулярные течению и поэтому они могут переходить из одного слоя в другой.
Характер течения зависит от безразмерной величины - числа Рейнольдеса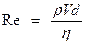 
, где r - плотность жидкости, V - скорость жидкости, d - характерный размер (например, диаметр трубы), η - вязкость. При Re < 1000 наблюдается ламинарное течение, а при Re > 1000 наблюдается турбулентное течение.