Цели обучения в 1 четверти. Алгебра и начала анализа 11 кл ЕМН
А Первообразная и интеграл
11.4.1.1 - знать определение первообразной функции и неопределенного интеграла;
11.4.1.2 - знать и применять свойства неопределенного интеграла;
11.4.1.3 - знать основные неопределенные интегралы:
1. 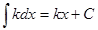 2.
2. 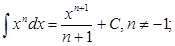 3.
3. 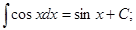 4.
4. 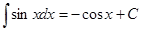 ;
5. ;
5. 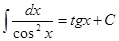 ;
6. ;
6. 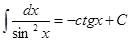 , и применять их при решении задач; , и применять их при решении задач;
|
| 11.4.1.4 - находить интеграл, используя метод замены переменной; 11.4.1.5 - находить интеграл, используя метод интегрирования по частям; |
| 11.4.1.6 - знать определение криволинейной трапеции и применять формулу Ньютона-Лейбница для нахождения её площади; |
| 11.4.1.7 - знать понятие определённого интеграла, уметь вычислять определённый интеграл; 11.4.1.8 - вычислять площадь плоской фигуры, ограниченной заданными линиями; 11.4.1.9 - знать и применять формулу вычисления объема тела вращения с помощью определенного интеграла; 11.4.2.1 - применять определённый интеграл для решения физических задач на вычисление работы и расстояния; СОР№1 11.1В Элементы математической статистики |
| 11.4.2.2 - знать и понимать основные термины математической статистики; |
| 11.3.3.1 - знать и понимать основные термины математической статистики; 11.3.3.2 - обрабатывать выборочные данные для составления дискретных и интервальных вариационных рядов; 11.3.3.3 - анализировать данные вариационного ряда в соответствии с заданным условием; |
| 11.3.3.4 - оценивать числовые характеристики случайных величин по выборочным данным. СОЧ №1 |
Повторение курса алгебры и начал анализа 10 кл
1. Функция, ее свойства. Графики изученных элементарных функций, их преобразования на координатной плоскости
2. Дробно-линейная функция
3. Сложная и обратная функции
4. Определение обратных тригонометрических функций, их свойства
5. Решение простейших тригонометрических уравнений (общие и частные случаи)
6. Методы решения тригонометрических уравнений
7. Решение простейших тригонометрических неравенств (на тригонометрическом круге)
8. Методы решения тригонометрических неравенств
9. Элементы комбинаторики (сочетания, перестановки, размещения без повторений и с повторениями; Бином Ньютона)
10. Вероятность события (классическое определение; условная вероятность; формулы сложения и умножения вероятностей, схема Бернулли)
11. Многочлены (методы разложения на множители; метод неопределенных коэффициентов; схема Горнера; теорема Безу; теорема о рациональном корне многочлена с целыми коэффициентами; уравнения высших степеней (симметрические и возвратные); обобщенная теорема Виета)
12. Нахождение пределов, раскрытие неопределенностей
13. Асимптоты графиков функций
14. Определение производной и дифференциала функции
15. Правила нахождения производных
16. Производные основных элементарных функций. Производная сложной функции
17. Геометрический и физический смысл производной
18. Уравнение касательной и нормали
19. Критические точки и точки экстремума функции. Монотонность функции
20. Точки перегиба, промежутки вогнутости (выпуклости) функции
21. Наибольшее и наименьшее значение функции
22. Непрерывные и дискретные случайные величины
23. Закон распределения ДСВ, числовые характеристики СВ, виды распределений случайной величины: биноминальное, геометрическое, гипергеометрическое