Программирования на языке паскаль

Основы

Программирования на языке паскаль

Методические указания

К лабораторным работам

Министерство образования и науки Российской Федерации

Балтийский государственный технический университет «Военмех»

Институт систем управления и управляющих систем

Кафедра информационных систем и компьютерных технологий

Основы
программирования
на языке паскаль

Методические указания

к лабораторным работам

Санкт-Петербург

Составители: Т.И. Лазарева, доц.; И.В. Мартынова, доц;
И.К. Ракова, канд. техн. наук, доц.

 

УДК 004.438 (075.8)

О75

	О75

УДК 004.438 (075.8)

 

Р е ц е н з е н т канд. техн. наук, проф. Н.Н. Смирнова

Утверждено
редакционно-издательским
советом университета

 

ã Составители, 2010

ã БГТУ, 2010

 

Общие положения

 

Предлагаемые лабораторные работы соответствуют темам лекций и содержат в себе по 22 варианта индивидуальных заданий, включающих несколько задач, предназначенных для решения.

Варианты заданий выдаются студентам заранее с тем, чтобы они имели возможность подготовиться к выполнению работы: просмотреть теоретический материал по теме и продумать алгоритмы решения задач. Каждую программу в работающем виде (после отладки и тестирования) студент должен показать преподавателю, после чего работа подлежит защите. К защите студент обязан подготовить отчет, который включает титульный лист, формулировку задания, алгоритм решения задачи, листинг программы и результаты тестирования. Пример оформления отчета приведен в приложении.

Защита лабораторной работы состоит из двух частей: практической и теоретической. В практической части студент должен объяснить принципы работы представленных им программ и продемонстрировать навыки программирования, в теоретической – ответить на вопросы по теме работы. При подготовке к защите рекомендуется ответить на контрольные вопросы.

 

Лабораторная работа № 1

Структура программы на языке Паскаль.
Программирование линейных алгоритмов

Цель работы – изучить структуру программы, научиться выполнять программу в среде Turbo Pascal, освоить арифметические операции языка Паскаль, получить навыки составления арифметических выражений и использования операторов присваивания и ввода/вывода.

 

Постановка задачи

 

Набрать в среде Turbo Pascal текст предложенной программы (приведен ниже) и выполнить ее несколько раз с различными исходными данными. Затем составить и выполнить программу согласно индивидуальному варианту. На экран вывести исходные данные и результат. Использовать форматный вывод.

 

Последовательность действий

 

1. Загрузите программу-оболочку VolkovCommander и сделайте текущим свой каталог.

2. Клавишей < F2 > откройте пользовательское меню и выберите в нем пункт Turbo Pascal.

3. В открывшемся окне интегрированной среды Turbo Pascal выберите пункт меню File/New.

4. Откроется окно текстового редактора среды Turbo Pascal (с синим фоном), в котором можно набирать исходный текст программы на языке Паскаль. Наберите в нем нижеприведенный текст программы для нахождения среднего арифметического и среднего геометрического значения двух заданных чисел.

 

Program First;

Var

a, b, sa,sg: real;

Begin

Writeln (‘Введите два числа:’);

Readln (a,b);

sa:= (a+b)/2;

sg:= sqrt(a*b);

Writeln (‘Ср. арифметическое=’, sa);

Writeln(‘Ср. геометрическое=’, sg);

End.

5. Далее следует сохранить в файле на диске набранный текст программы. Для этого используется пункт меню File/Save As.

6. Оттранслируйте программу и запустите ее на выполнение с помощью пункта меню Run/Run (можно сначала Compile/Compile, затем Run/Run). Если текст программы содержит синтаксические ошибки, то в верхней строке окна редактора появится сообщение об ошибке, а курсор укажет ее предположительное местоположение. После исправления ошибки надо вновь сохранить программу (File/Save) и запустить ее на трансляцию и выполнение (Run/Run). Когда все ошибки в программе будут исправлены, она начнет выполняться.

7. Когда выполнение программы дойдет до ввода данных, ее выполнение приостановится, произойдет переключение к пользовательскому экрану (на черном фоне). Для набранной программы следует ввести два исходных данных. Два числа (для a и для b) можно вводить или в одной строке через пробел, или каждое с новой строки. После ввода исходных данных должна быть нажата клавиша <Enter>.

8. Когда выполнение программы закончится, на экране вновь появится окно редактора с исходным текстом программы. Чтобы увидеть выведенные на экран результаты работы программы, воспользуйтесь пунктом меню Debug/User screen.

9. Выполните программу несколько раз с разными исходными данными. Убедитесь в правильности ее работы.

10. Внесите изменения в программу, например добавьте указание формата вывода в оператор вывода:

 

Writeln (‘Ср. арифметическое=’, sa:5:2);

Writeln(‘Ср. геометрическое=’, sg:5:2);

 

Сохраните измененный вариант программы (File/Save) и выполните ее заново (Run/Run).

11. Выйдите из среды Turbo Pascal с помощью пункта меню File/ Exit.

 

Варианты заданий

 

 

Вариант 1

 

Вариант 2

 

Вариант 3

 

Вариант 4

 

Вариант 5

 

Вариант 6

Вариант 7

 

Вариант 8

 

Вариант 9

 

Вариант 10

 

Вариант 11

 

Вариант 12

Вариант 13

Z=

 

Вариант 14

 

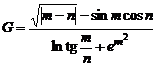
Вариант 15

 

Вариант 16

 

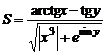
Вариант 17

 

Вариант 18

Вариант 19

 

Вариант 20

 

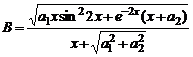
Вариант 21

Z=

 

Вариант 22

 

 

Контрольные вопросы

 

1. Какова структура программы на языке Паскаль?

2. Чем разделяются операторы в программе на Паскале?

3. Какие описательные разделы может содержать программа на Паскале? В каком порядке они должны следовать в программе?

4. Каковы правила составления идентификаторов?

5. Чем отличаются зарезервированные слова от стандартных идентификаторов?

6. Что определяет тип данного?

7. Чем отличаются данные типа real от данных типа integer?

8. Что такое константа? Назовите виды констант.

9. Как записываются константы в программе?

10. Каковы способы записи вещественных чисел в программе?

11. Что такое переменная?

12. Какие типы относятся к порядковым? Что их отличает от других?

13. Как работает оператор присваивания?

14. Что такое выражение?

15. Какие операции относятся к арифметическим? Укажите их приоритет.

16. Для чего используются круглые скобки в выражениях?

17. Какие операции применимы к целочисленным данным?

18. Какие операции применимы к вещественным данным?

19. Какие операции отношения вы знаете? Какой тип имеет их результат?

20. Что будет, если пропустить знак умножения при записи оператора с:=a*b?

21. Для какой цели могут использоваться фигурные скобки в программе на Паскале?

22. Где и как в программе можно записать комментарий?

23. Каково назначение процедур read и readln? Чем они различаются?

24. Какие элементы может содержать список ввода? Какого типа они могут быть?

25. Каково назначение процедур write и writeln?

26. Какие элементы может содержать список вывода? Какого типа они могут быть?

27. Сколько элементов может содержать список ввода? Что будет, если он будет пустым?

28. Какое соответствие должно быть между типами переменных списка ввода и типами вводимых данных?

29. Как записывается формат вывода? Что он определяет?

30. В чем состоит действие процедур writeln и readln без параметров?

 

Лабораторная работа № 2

 

Программирование ветвлений

Цель работы – освоить операции отношения, логические операции, научиться составлять и использовать логические выражения и изучить работу условного оператора.

 

Постановка задачи

 

Написать три программы согласно индивидуальному варианту. В первой программе вычислить и вывести значение логического выражения. Во второй программе вычислить значение функции, используя условный оператор. В третьей программе использовать вложенный условный оператор.

 

Варианты заданий

 

Вариант 1

1. Вывести на экран значение логического выражения, которое должно быть равно true, если Х лежит вне отрезков [2,5]и [-1,1]и false – в противном случае.

2.

3. Вывести на экран номер четверти, которой принадлежит точка с координатами (x, y), или указать, какой оси принадлежит эта точка.

 

Вариант 2

1. Покупатель хочет купить игрушку ребенку в возрасте А лет по цене от С1 до С2 рублей. Вывести на экран значение логического выражения, которое должно быть равно true, если ему подходит машинка стоимостью 250 руб., предназначенная для детей от 5 до 8 лет, и false – в противном случае.

2.

3. Даны три целых числа, найти среднее из них. Средним назовем число, которое больше наименьшего и меньше наибольшего.

 

Вариант 3

1. Даны три целых числа: K, M и N. Вывести на экран значение логического выражения, которое должно быть равно true, если среди заданных чисел есть хотя бы два четных, и false – в противном случае.

2.

3. Даны стороны треугольника. Определить его вид: равносторонний, равнобедренный или разносторонний, и вывести сообщение об этом. Кроме того, если треугольник равносторонний, то найти его высоту, если он равнобедренный – его полупериметр, в противном случае – его наибольшую сторону.

 

Вариант 4

1. Вывести на экран значение логического выражения, которое принимает значение true, если К является двухзначным числом, кратным пяти и false – в противном случае.

2.

3. Даны два целых числа. Если они оба положительны, то большее из них заменить их средним арифметическим; если оба отрицательны, то поменять знак у меньшего из них; если иначе – каждое из них удвоить.

 

Вариант 5

1. Вывести на экран значение логического выражения, которое должно быть равно true, если кирпич, имеющий форму прямоугольного параллелепипеда с ребрами a,b,c, может пройти через квадратное отверстие со стороной d, и false – в противном случае.

2.

3. Даны два целых числа. Если они оба четны, то большее из них поделить на 2; если оба нечетны, то каждое умножить на 2; в противном случае нечетное из чисел увеличить на 1.

Вариант 6

1. Вывести на экран значение логического выражения, которое должно быть равно true, если треугольник со сторонами a, b, c является равнобедренным, и false – в противном случае.

2.

3. Даны два числа. Если они оба положительны, то поменять знак у большего из них; если оба отрицательны, то первое умножить на 2, а второе на 3; в противном случае меньшее заменить их полусуммой, а большее уменьшить на 1.

 

Вариант 7

1. Вывести на экран значение логического выражения, которое должно быть равно true, если среди четырёх заданных чисел a, b, c, d наименьшим является а, и false – в противном случае.

2.

3. Даны координаты двух точек на плоскости. Если хотя бы одна из них лежит на какой-нибудь оси, то вывести сообщение об этом; если обе находятся в одной четверти, то найти и вывести расстояние между ними; если иначе, то найти точку, наиболее удаленную от центра координат.

 

Вариант 8

1. Вывести на экран значение логического выражения, которое должно быть равно true, если точка с координатами (х,у)принадлежит кольцу с внутренним радиусом R, наружным радиусом R ₁ и центром в начале координат, и false – в противном случае.

2.

3. Даны три целых числа. Наибольшее из них удвоить, у наименьшего поменять знак на противоположный, среднее по значению заменить полусуммой двух других.

 

Вариант 9

1. Вывести на экран значение логического выражения, которое должно быть равно true, если заданное натуральное число К является трехзначным числом, кратным трем, и false – в противном случае.

2.

3. Даны три целых числа. Если все они равны, то оставить их без изменения; если образуют монотонную (т.е. либо возрастающую, либо убывающую) последовательность, то заменить последнее число так, чтобы заданные числа образовали арифметическую прогрессию (считая, что первые два числа являются первыми членами прогрессии); если иначе, то второе число заменить полусуммой первого и третьего чисел.

 

 

Вариант 10

1. Вывести на экран значение логического выражения,
которое должно быть равно true или false в зависимости от того, может ли кирпич, имеющий форму прямоугольного параллеле-пипеда с ребрами a,b,c, пройти через круглое отверстие с диаметром d.

 

2.

3. Дано натуральное двухзначное число. Если цифры в нем одинаковы, то уменьшить заданное число на 1; если цифры разные, то меньшую из них заменить в заданном числе нулём.

 

Вариант 11

1. Вывести на экран значение логического выражения, которое должно быть равно true, если точка Х на числовой оси попадает в один из двух отрезков [ a, b ]и [ c, d ],и false – в противном случае.

 

 

2.

 

3. Даны два числа. Если они оба отрицательны, то первое уменьшить на 1, а второе увеличить на 1; если оба положительны, то большее из них удвоить, а меньшее утроить; в противном случае отрицательное из чисел заменить его абсолютным значением.

 

 

Вариант 12

1. Даны два числа: A и B. Вывести на экран значение логического выражения, которое должно быть равно true, если оба числа находятся в интервале (X, Y),и false – в противном случае.

 

2.

 

3. Даны стороны треугольника. Определить его вид: равносторонний, равнобедренный или разносторонний, и вывести сообщение об этом. Кроме того, если треугольник равносторонний, то найти его площадь, если он равнобедренный – его периметр, в противном случае – его наименьшую сторону.

 

 

Вариант 13

1. Даны четыре числа: a, b, c и d. Вывести на экран значение логического выражения, которое должно быть равно true, если четырехугольник со сторонами a, b, c, d является ромбом (у ромба все стороны равны), и false – в противном случае.

 

2.

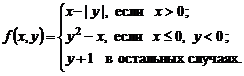
3. Даны вещественное число a и целое b. Вычислить 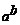, используя формулу 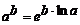. Учесть случаи, когда

 

Вариант 14

1. Вывести на экран значение логического выражения, которое должно быть равно true, если X лежит вне отрезка [ a, b ]и является положительным числом, и false – в противном случае.

2.

3. Даны три числа. Если все они равны, то оставить их без изменения; если образуют возрастающую последовательность, то уменьшить каждое из чисел на единицу; если образуют убывающую последовательность, то второе число заменить полусуммой первого и третьего чисел; если иначе, то поменять местами первое и последнее числа.

 

Вариант 15

1. Вывести на экран значение логического выражения, которое должно быть равно true, если точка с координатами (х 1, у 1) принадлежит заштрихованной области, и false – в противном случае.

 

2.

3. Написать программу для решения неравенства 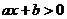относительно x для любых значений a и b.

Вариант 16

1. Вывести на экран значение логического выражения, которое должно быть равно true, если две точки с координатами (x1, y1) и (x2, y2) лежат в одной четверти, и false – в противном случае.

2.

3. Написать программу для решения уравнения относительно x для любых значений a и b.

 

Вариант 17

1. Вывести на экран значение логического выражения, которое должно быть равно true, если среди трех заданных чисел А, В и С есть хотя бы два нечетных, и false – в противном случае.

2.

3. Написать программу для решения неравенства относительно x для любых ненулевых значений a и b.

 

Вариант 18

1. Вывести на экран значение логического выражения, которое должно быть равно true, если заданное двузначное натуральное число N делится на 7 или цифра 7 входит в десятичную запись этого числа, и false – в противном случае.

2.

3. Написать программу для решения неравенства относительно x для любых ненулевых значений a, b и c.

Вариант 19

1. Даны четыре числа: a, b, c и d. Вывести на экран значение логического выражения, которое должно быть равно true, если среди них есть одинаковые по модулю, и false – в противном случае.

 

2.

 

3. Дано натуральное трехзначное число. Если цифры в нем одинаковы, то уменьшить заданное число на 10; если цифры разные, то меньшую из них заменить в заданном числе нулём.

 

Вариант 20

1. На шахматной доске стоят белый и черный ферзи (ферзь бьет по вертикали, горизонтали и диагонали). Их координаты заданы парами чисел (x1, y1) и (x2, y2). Вывести на экран значение логического выражения, которое истинно, если ферзи угрожают друг другу, и ложно в противном случае.

 

2.

 

3. Дано натуральное трехзначное число. Если все цифры в нем одинаковы, то оставить заданное число без изменения; если все цифры разные, то меньшую из них заменить в заданном числе нулём; если две цифры одинаковые, то получить число с обратным порядком цифр.

 

Вариант 21

1. Две даты заданы следующим образом: d1, m1, y1 – соответственно день, месяц и год первой даты; d2, m2, y2 – второй даты. Вывести на экран значение логического выражения, которое должно быть равно true, если первая дата является более поздней, чем вторая, и false – в противном случае.

2.

3. Даны три числа. Если они все отрицательны, то первое уменьшить на 3, а третье увеличить на 3; если все положитель-
ны, то большее из них удвоить, а меньшее утроить; в против-
ном случае отрицательные числа заменить их абсолютными значениями.

 

Вариант 22

1. Вывести на экран значение логического выражения, кото-рое должно быть равно true, если из трех заданных чисел a, b, c
никакие два не различаются больше, чем на 3, и false – в противном случае.

2.

3. Даны три числа. Если они все положительны, то поменять знак у большего из них; если все отрицательны, то каждое умножить на 2; если только два из них положительны, то отрицательное число заменить полусуммой положительных чисел; в противном случае числа не менять.

 

 

Контрольные вопросы

 

1. Каков синтаксис условного оператора?

2. Каков тип выражения, определяющего условие в условном операторе?

3. Какие операции относятся к операциям отношения, какие к логическим операциям?

4. Какие логические операции Вы знаете? Объясните их смысл и укажите их приоритеты.

5. Какие значения может принимать логическая переменная? Какие операции к ней применимы?

6. Можно ли вводить и выводить данные логического типа?

7. Почему при записи составного условия простые условия (отношения) должны заключаться в скобки?

8. Какие операции имеют самый высокий приоритет: арифметические, логические или операции отношения? У каких операций самый низкий приоритет?

9. Почему логический тип относится к порядковым?

10. Может ли логическое выражение содержать несколько операций? Какие операции могут в нем использоваться?

11. Как работает условный оператор?

12. Что такое составной оператор? Для чего он используется?

13. Что представляет собой вложенный условный оператор?
Каковы особенности его использования?

14. Для чего применяется оператор выбора? Каков его синтаксис?

15. Как будет выглядеть условный оператор, заменяющий оператор выбора?

 

Лабораторная работа № 3

 

Программирование циклов

Цель работы – научиться различать арифметические и итерационные циклы и реализовывать циклические алгоритмы с помощью операторов цикла for, while и repeat.

 

Постановка задачи

 

Написать четыре программы согласно индивидуальному варианту. В первой программе смоделировать арифметический цикл с помощью оператора цикла for. Во второй программе использовать циклы while или repeat. В третьей программе вычислить бесконечную сумму с заданной точностью, используя рекуррентные зависимости, в четвертой – использовать при написании программы конструкцию “цикл в цикле”. На экран вывести исходные данные и результат. Использовать форматный вывод. Ни в одной из программ массивы не использовать.

Варианты заданий

 

Вариант 1

1. Получить таблицу температур по Цельсию от 0° до 100° и их эквивалентов по шкале Фаренгейта, используя для перевода формулу .

2. Найти первое число Фибоначчи, большее заданного n (n> 1).

3. Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10^-4, , и значение функции (для проверки) f=e^-x. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Дано целое k > 2. Напечатать все простые числа из диапазона [2, k ].

Вариант 2

1. Вычислить первые 20чисел Фибоначчи F_n=F_{n- 1} +F_{n- 2}, F ₀ =F ₁ = 1.

2. Пусть последовательность определяется следующим образом x ₀=1, , k= 1,2, …. Найти первый член x_n, для которого выполняется условие .

3. Вычислить значение суммы бесконечного ряда 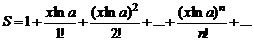, с точностью до члена
ряда, меньшего e=10^-4, и значение функции (для проверки)
f=a^x; учесть, что функция определена при 0,1 < = x < = 1. Вывес-
ти на экран значение указанной функции и значение суммы
ряда. Оба значения должны совпадать.

4. Последовательно вводятся вещественные числа. Признаком окончания ввода является отрицательное число или нуль. Вычислить произведение (Х- 2 )(Х- 4 )(Х- 6 )…(Х- 22 ) для каждого из введенных чисел Х.

 

Вариант 3

1. Вычислить F =1!+2!+…+ n!

2. Дано натуральное число n. Составить программу для сравнения цифр старшего и младшего разрядов этого числа.

3. Вычислить значение суммы бесконечного ряда с точностью до члена ряда, по модулю меньшего e=10^-3, и значение функции (для проверки) f=e^x; учесть, что функция определена при 1 < = x < = 2. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Последовательно вводятся числа a (до тех пор, пока не будет введен 0). Для каждого из них вычислить значение функции y=sinx+a при х, изменяющемся на отрезке от – до с шагом 0,1.

 

Вариант 4

1. Дано 20 целых чисел, которые вводятся по одному. Получите сумму тех из них, которые нечетны и отрицательны.

2. Дано натуральное число n. Составить программу для определения количества цифр в этом числе.

3. Вычислить значение суммы бесконечного ряда
, с точностью до члена ряда, по модулю меньшего e=10^-5, и значение функции (для проверки) f = ; учесть, что -3,14<= x <= 3 14. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Написать программу для поиска N (N вводится) первых простых чисел.

 

Вариант 5

1. Вычислить a(a-n)(a- 2 n)…(a-n ² ). Вещественное а и целое n вводятся с клавиатуры.

2. Вычислить за сколько лет в банке «Сибнефть» при начальном вкладе W и процентах годового прироста Pr будет накоплена сумма Sum.

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-3, , и значение функции (для проверки) . Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Последовательно вводятся n натуральных чисел (n <= 10). Вычислить сумму тех из них, у которых первая цифра равна последней.

 

Вариант 6

1. Последовательно вводятся n действительных чисел (n<= 20). Вычислить среднее арифметическое этих чисел.

2. Составить программу для определения, является ли натуральное число k степенью числа 3(операцию возведения в степень не использовать).

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-5 s= и значение функции (для проверки) ; учесть, что функция определена при x ²>1. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Для каждого из n (n ≤10)значений переменной х, изменяющейся от – b до b с постоянным шагом, вычислить значение произведения Р=х* (х+ 0,2) *(х+ 0,4) *…* (х+ 1,8).

Вариант 7

1. Вывести таблицу значений функции у =2sin x +cos2 x на отрезке от a = - до b = для значений аргумента x_i = a+ih, i =0,1,2,… n; h = ; n =10.

2. Дано целое m > 1. Получить наибольшее целое k, при котором 4 ^k < m.

3. Вычислить значение суммы бесконечного ряда 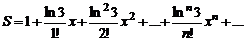, с точностью до члена ряда, по модулю меньшего e=10^-4, и значение функции (для проверки) f= 3 ^x, учесть, что функция определена при 0< = x <=1. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Дано k натуральных чисел. Определить, сколько из них совершенных. Совершенным называется число, равное сумме всех своих делителей, включая 1 и не включая само число.

 

Вариант 8

1. Последовательно вводятся n (n ≤10)целых чисел. Получить сумму тех чисел, которые принадлежат заданному интервалу (а,b).

2. Дано натуральное n. Составить программу для поиска первой цифры этого числа.

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 , и значение функции (для проверки) ; учесть, что функция определена при . Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Последовательно вводятся целые положительные числа. Для каждого числа выяснить, является ли оно факториалом какого-либо числа. Если да, то вывести число, факториалом которого является введенное, если нет, вывести сообщение об этом. Признаком конца ввода является ввод нуля.

 

Вариант 9

1. Вводится последовательность из n целых чисел. Найти максимальное среди них.

2. Дано натуральное число n. Выяснить, является ли оно степенью числа 5 (операцию возведения в степень не использовать).

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 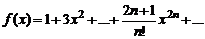, и значение функции (для проверки) , учесть, что функция определена при . Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Для каждого из 20 значений переменной x, изменяющейся от -a до a с постоянным шагом, вычислить значение суммы .

 

Вариант 10

1. Даны натуральное число n и вещественное х. Вычислить .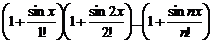

2. Спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от пробега предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км?

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 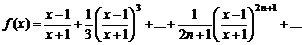, и значение функции (для проверки) 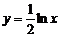; учесть, что функция определена при 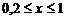. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Найти натуральное число в диапазоне от 2 до n (n <=500) с максимальной суммой делителей (само число в сумму не включать).

 

Вариант 11

1. Даны натуральные числа a и b. Определить все числа, кратные a и b, меньшие a*b (a и b должны быть больше 10).

2. Факториал некоторого числа равен p. Найти это число.

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 и значение функции (для проверки) f= sin 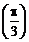. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Для заданных x= 2, 3, 4,5, 6, 7, 8, 9, 10 вычислить значение y= по рекуррентному соотношению Ньютона: , y ₀ = 0,3 x. Вычисления продолжать до тех пор, пока не выполнится условие 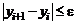, e=10^-4. Подсчитать, сколько итераций надо выполнить для этого.

 

 

Вариант 12

1. Вычислить и вывести n членов арифметической прогрессии с первым членом а и разностью прогрессии р. Определить их произведение.

2. Дано действительное а. Вычислить .

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 , и значение функции (для проверки) учесть, что функция определена при 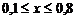. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Дано положительное число с. Для каждого значения х= 2,3,4,…,7 найти такое наибольшее целое к, при котором х^к не превышает заданное с. Операцию возведения в степень не использовать.

 

 

Вариант 13

1. Для натурального числа n получить все его натуральные нечетные делители.

2. Определить наибольшее натуральное число, факториал которого не превышает 10⁵.

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-4 , и значение функции (для проверки) 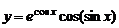; учесть, что функция определена при 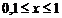. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Дано натуральное число n. Вычислить S= 1+2²+3³+…+ nⁿ. Операцию возведения в степень не использовать.

 

 

Вариант 14

1. Дано 10 вещественных чисел. Определить, образуют ли они возрастающую последовательность.

2. Последовательно вводятся числа до тех пор, пока не будет введен 0. Найти количество чисел, которые не принадлежат заданному интервалу (а,b).

3. Вычислить значение суммы бесконечного ряда 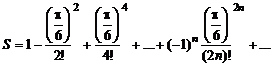с заданной точностью e=10^-4 и значение функции (для проверки) 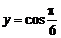. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны совпадать.

4. Даны натуральные числа а, b (а<b). Получить все простые числа p, удовлетворяющие неравенству a<p<b.

 

Вариант 15

1. Дано целое n (n<= 30) и вещественное x. Вычислить:
y=x + 2 x ² + 3 x ³ +…+ nxⁿ.

2. Вывести на экран значение первого отрицательного члена последовательности cos(ctg(n)), n= 1,2,3,…. Отрицательные члены в этой последовательности обязательно есть.

3. Вычислить значение суммы бесконечного ряда с заданной точностью e=10^-5 , и значение функции (для проверки) ; учесть, что функция определена при x ²<1. Вывести на экран значение указанной функции и значение суммы ряда. Оба значения должны сов