Содержание
Часть 1. Расчет полей допусков размеров детали. 3
Часть 2. Расчет сборочных размерных цепей методами взаимозаменяемости. 3
Часть 3. Обработка многократных измерений. 3
Список литературы: 3
Задача №1
Рассчитать параметры посадки Æ19R7 /h6; написать все виды обозначения предельных отклонений размеров на конструкторских и рабочих чертежах; рассчитать калибры для проверки отверстия и вала заданной посадки; дать рабочие чертежи калибров.
Для расчета дана посадка с натягом в системе вала.
Отклонения отверстия и вала по ГОСТ 25347-82
ЕS=-20 мкм еs= 0 мкм
ЕI= -41 мкм еi= –13 мкм
Схема расположения полей допусков
2. Предельные размеры:
Dmax = N+ ES= 19 + (-0,020) =18,980 мм
Dmin = N + EI = 34 +(-0,041) = 18,959 мм
dmax = N + еs = 19 +0 = 19,000 мм
dmin = N + ei = 19 + (–0,013) = 18,987мм
3. Допуски отверстия и вала:
ТD = Dmax – Dmin = 18,980 – 18,959 = 0,021 мм
Тd = dmax – dmin = 19,000 – 18,987 = 0,013 мм
Или
ТD = ES – EI = -0,020 –(- 0,041) = 0,021 мм
Тd = еs – ei = 0– (–0,013) = 0,013 мм
4. Натяги:
Nmax = dmax – Dmin = 19,000 – 18,959 = 0,041 мм
Nmin = dmin - Dmax = 18,987 – 18,980 = 0,007 мм
5. Средний натяг:
Nc = (Nmax + Nmin)/2 = (0,041+0,007)/2= 0,024 мм.
6. Допуск натяга (посадки):
ТN = Nmax – Nmin = 0,041 – 0,007= 0,034 мм
Или
ТN = ТD + Тd = 0,021+0,013 = 0,034 мм
7.Обозначение предельных отклонений размеров на конструкторских чертежах:
| а) условное обозначение полей допусков: |
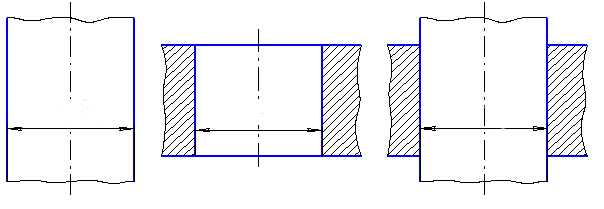
б) числовые значения предельных отклонений:

в) условное обозначение полей допусков и числовых значений предельных отклонений:

8. Обозначение размеров на рабочих чертежах

Задача №2. Расчет размерных цепей
Требуется:
1) Определить допуски и отклонения всех размеров деталей, влияющих на величину указанного зазора(прямая величина);
2) По заданным значениям размеров всех деталей, влияющих на зазор А, определить предельные значения указанного зазора(обратная задача) и сравнить его с заданными значениями.
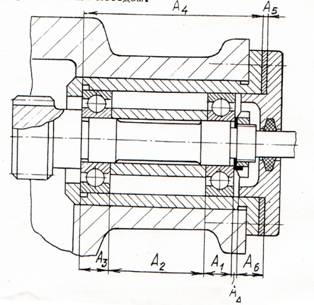
Задача №1
Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера,
равное А =0+0.6
На детали, входящие в сборочный чертёж, назначены следующие значения номинальных размеров N1=29мм, N2=186мм, N3=29мм, N4=264мм, N5=6мм, N6=26мм.
1) Согласно заданию имеем
N =0мм,
TΔ =0.6-0=0.6мм
Ec= 
Аmax=0+0,6=0,6мм
Аmin=0+0=0мм
2) Составим график размерной цепи:
3) Составим уравнение размерной цепи
А =ξ1А1+ξ2А2+ξ3А3+ξ4А4+ξ5А5+ξ6А6;
Значения передаточных отношений
| Обозначение передаточных отношений | ξ1 | ξ2 | ξ 3 | ξ4 | ξ5 | ξ6 |
| Численное значение ξ | -1 | -1 | -1 | +1 | +1 | -1 |
4) Произведем проверку правильности назначения номинальных значений составляющих размеров:
NΔ =-29-186-29+264+6-26=0
Так как по условию задачи NΔ =0, следовательно, номинальные размеры назначены правильно.
5) Осуществим увязку допусков, для чего исходя из величины Т рассчитаем допуски составляющих размеров.
Так как в допуск входят подшипники качения, допуски которых являются заданными, то для определения величины ас воспользуемся зависимостью
 где TD - допуск замыкающего размера, мкм;
где TD - допуск замыкающего размера, мкм;
ij – значение единицы допуска, мкм.
C учетом того,что допуск ширины равен 0,12 мм, имеем Т1=Т3=0,12мм.

6) По приложению А устанавливаем, что такому значению ас соответствует точность, лежащая между 9 и 10 квалитетами. Примем для всех размеров 9 квалитет, тогда
Т2=0,115мм; Т4=0,130мм; Т5=0,030мм; Т6=0,052мм.
7) Произведем проверку правильности назначения допусков составляющих размеров по уравнению 
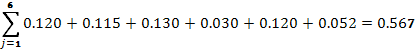 мм
мм
Полученная сумма допусков меньше заданного допуска замыкающего размера на величину, равную 0,033мм, что составляет 5.5% от ТΔ. Следовательно, допуски можно оставить без изменения.
8) Осуществим увязку средних отклонений, для чего примем следующий характер расположения полей допусков составляющих размеров.
А1=A3=29 -0.12мм
A2=186h9(-0.115)мм
A4=264Js9(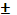 0.065)мм
0.065)мм
А5=6h9(-0.030)мм
A6=26Js9(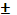 0.026)мм
0.026)мм
| Обозначение размера | РАЗМЕР | ξ | Ес | ξЕс |
| А1 | 29 -0.12 | -1 | -0,0600 | 0,060 |
| А2 | 186h9(-0.115) | -1 | -0.0575 | 0.0575 |
| А3 | 29 -0.12 | -1 | -0.0600 | 0,0600 |
| А4 | 264Js9(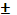 0.065) 0.065)
| +1 | ||
| А5 | 6h9(-0.030) | +1 | -0.0150 | -0.0150 |
| А6 | 26Js9(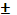 0.026) 0.026)
| -1 |
По уравнению  найдем среднее отклонение замыкающего размера и сравним его с заданным
найдем среднее отклонение замыкающего размера и сравним его с заданным
мм
Так как полученное значение не совпадает с заданным, то произведем увязку средних отклонений за счет среднего отклонения А2, принятого в качестве увязочного. Величину среднего отклонения размера А2 из уравнения  .Т.е. +0,30=-0,060+0,060-0,0150=+0,195мм
.Т.е. +0,30=-0,060+0,060-0,0150=+0,195мм
Предельные отклонения А2:
ES2=+0.195+0.5*0.6=0.495 мм
EI2=+0.195-0.5*0.6=-0.105 мм
Таким образом A2=186+0.495
Задача №2
Найти предельные значения замыкающего размера  при значениях составляющих размеров, полученных в результате решения задачи №1. Расчет произвести методом полной взаимозаменяемости.
при значениях составляющих размеров, полученных в результате решения задачи №1. Расчет произвести методом полной взаимозаменяемости.
Сведем данные для расчета в таблицу
| Обозначение размера | размер | 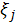
| 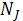
| 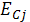
| 
| 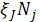
| 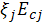
| 
|
| A1 | 29 -0.12 | -1 | -0.060 | 0.120 | -29 | 0.0600 | 0.0600 | |
| A2 | 186h9(-0.115) | -1 | 0.195 | 0.115 | -186 | 0.0575 | 0.0575 | |
| A3 | 29 -0.12 | -1 | -0.060 | 0.120 | -29 | 0.0600 | 0.0600 | |
| A4 | 264Js9(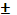 0.065) 0.065)
| +1 | 0.130 | |||||
| A5 | 6h9(-0.030) | +1 | -0.015 | 0.030 | -0.015 | 0.0150 | ||
| A6 | 26Js9(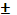 0.026) 0.026)
| -1 | 0.052 | -26 |
1) Номинальное значение замыкающего размера
N Δ=-29-186-29+264+6-26=0 мм
2) Среднее отклонение замыкающего размера
Ec=0.060+0.195+0.060+0-0.015-0=0.3
3) Допуск замыкающего размера
T Δ=0.120+0.115+0.120+0.130+0.030+0.052=0.567мм
Предельные отклонения замыкающего размера
Сравниваем полученные результаты с заданными
=
Осуществим поверку допустимости расчетных значений

Полученные значения не превышают установленных 10%. Следовательно, изменения предельных отклонений составляющих размеров не требуется.
Задача№3
Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера,
равное А=0+0.6мм. Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%
на детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров: N1=29мм, N2=186мм, N3=29мм, N4=264мм, N5=6мм, N6=26мм.
1) Согласно заданию имеем
N =0мм,
TΔ=0.6-0=0.6мм
Ec= 
Аmax=0+0,6=0,6мм
Аmin=0+0=0мм
2) Составим график размерной цепи:
3)Составим уравнение размерной цепи
А =ξ1А1+ξ2А2+ξ3А3+ξ4А4+ξ5А5+ξ6А6;
Значения передаточных отношений
| Обозначение передаточных отношений | ξ1 | ξ2 | ξ 3 | ξ4 | ξ5 | ξ6 |
| Численное значение ξ | -1 | -1 | -1 | +1 | +1 | -1 |
4)Произведем проверку правильности назначения номинальных значений составляющих размеров:
NΔ=-29-186-29+264+6-26=0
Так как по условию задачи NΔ=0, следовательно, номинальные размеры назначены правильно.
5)Осуществим увязку допусков, для чего исходя из величины Т рассчитаем допуски составляющих размеров.
Так как в допуск входят подшипники качения, допуски которых являются заданными, то для определения величины ас воспользуемся зависимостью  .
.
С учетом того,что допуск ширины подшипников равен 0,12мм, т.е А1=А3=0,12 мм
Следовательно 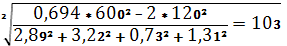
6) по приложению А устанавливаем, что полученное значение ас больше принятого для квалитета 11, но меньше для квалитета 12.
Установим для всех размеров допуски по 11 квалитету, тогда:
Т2=0,290 мм, Т4=0,320 мм, Т5=0,075мм, Т6=0,130 мм.
7) произведем проверку правильности назначения допусков составляющих размеров по уравнению
 =0.59 мм
=0.59 мм
Полученная сумма оказалась меньше заданного допуска замыкающего размера.
Расширим допуск А2  Т2=0,31мм
Т2=0,31мм
8) Произведем увязку средних отклонений. Увязку будем производить за счет среднего отклонения размера А2, принятого в качестве увязочного.
Примем следующий характер расположения полей допусков составляющих размеров
А1=А3=29-0,12мм
А4=264Js11(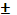 0,016)мм
0,016)мм
А5=6h(-0,015)мм
А6=26Js11(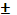 0.065)мм
0.065)мм
| обозначение | размер | ξi | ECJ | Tj | αi | αi 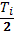
| Ecj+α 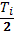
| ξ(Ecj+α 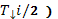
|
| A1 | 29-0,12 | -1 | -0,060 | 0,120 | +0,2 | 0,0120 | -0,048 | 0,048 |
| A2 | -1 | EC2 | 0,290 | +0,2 | 0,0290 | EC2+0,029 | (EC2+0,029) | |
| A3 | 29-0,12 | -1 | -0,060 | 0,120 | +0,2 | 0,0120 | -0,048 | 0,048 |
| A4 | 264Js11(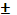 0,016) 0,016)
| +1 | 0,320 | |||||
| A5 | 6h(-0,015) | +1 | 0,0075 | 0,015 | +0,2 | 0,0015 | 0,009 | 0,009 |
| A6 | 26Js11(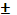 0.065) 0.065)
| -1 | 0,130 |
Найдем среднее отклонение размера А2
0,3=0,048+(Ес2+0,029)+0,048+0+0,009+0
Ес2=0,166 мм
ES2=0.166+0.5*0.29=0.311
EI2=0.166-0.5*0.29=0.021
A2=186+0,021
Задача№4
Найти предельные значения замыкающего размера А при значениях составляющих размеров, полученных в результате решения задачи №3. Расчет произвести вероятностным методом, исходя из допустимого процента брака на сборке, равного 0,27%
Сведем данные для расчета в таблицу
| Размер | ξi | ECJ | Tj | αi | αi 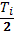
| Ecj+α 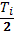
| ξ(Ecj+α 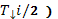
| | ξ| Tj | (| ξ| Tj)2 | |
| А1 | 29-0,12 | -1 | -0,060 | 0,120 | +0,2 | 0,0120 | -0,048 | 0,048 | 0.120 | 0.01440 |
| А2 | -1 | 0,166 | 0,290 | +0,2 | 0,0290 | EC2+0,029 | 0,195 | 0.290 | 0.03803 | |
| А3 | 29-0,12 | -1 | -0,060 | 0,120 | +0,2 | 0,0120 | -0,048 | 0,048 | 0.120 | 0.01440 |
| А4 | 264Js11(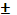 0,016) 0,016)
| +1 | 0,320 | 0.320 | 0.10240 | |||||
| А5 | 6h(-0,015) | +1 | 0,0075 | 0,015 | +0,2 | 0,0015 | 0,009 | 0,009 | 0.015 | 0.00225 |
| А6 | 26Js11(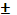 0.065) 0.065)
| -1 | 0,130 | 0.130 | 0.01690 |
1) Номинальное значение замыкающего размера
NΔ=-29-186-29+264+6-26=0мм
2) Среднее отклонение замыкающего размера
ЕсΔ=0,048+0,195+0,048+0+0,009+0=+0,3 мм
3) Допуск замыкающего размера
ТΔ=1,2  =0,58
=0,58 
4) Предельные отклонения замыкающего размера
АΔmax=0+0.3+0.5*0.6=0.6
AΔmin=0+0.3-0.5*0.6=0
5) Сравниваем полученные результаты с заданными
АΔmaxрасч=0,6=АΔmax задан=0,6
АΔmin расч=0=AΔminзадан=0
Следовательно, изменения предельных отклонений составляющих размеров не требуется.
Задача №3
Определить вид ЗРВ по критерию Пирсона;
Записать результат с доверительной вероятностью P=0.97
| 43,54 | 43,39 | 43,44 | 43,39 | 43,63 | 43,53 | 43,43 | 43,14 | 43,55 | 43,65 |
| 43,38 | 43,55 | 43,43 | 43,50 | 43,39 | 43,67 | 43,37 | 43,54 | 43,33 | 43,65 |
| 43,54 | 43,72 | 43,44 | 43,42 | 43,26 | 43,67 | 43,55 | 43,54 | 43,50 | 43,34 |
| 43,42 | 43,49 | 43,42 | 43,58 | 43,33 | 43,52 | 43,51 | 43,27 | 43,26 | 43,53 |
| 43,53 | 43,59 | 43,57 | 43,29 | 43,47 | 43,45 | 43,82 | 43,41 | 43,59 | 43,39 |
| 43,44 | 43,57 | 43,72 | 43,44 | 43,52 | 43,57 | 43,27 | 43,50 | 43,44 | 43,68 |
| 43,53 | 43,55 | 43,68 | 43,50 | 43,32 | 43,45 | 43,39 | 43,42 | 43,60 | 43,61 |
| 43,44 | 43,39 | 43,47 | 43,48 | 43,57 | 43,59 | 43,63 | 43,66 | 43,66 | 43,66 |
| 43,46 | 43,64 | 43,46 | 43,78 | 43,27 | 43,42 | 43,43 | 43,43 | 43,47 | 43,60 |
| 43,52 | 43,35 | 43,28 | 43,68 | 43,77 | 43,50 | 43,94 | 43,35 | 43,51 | 43,60 |
Отсортируем исходные данные по возрастанию
| Х | 43,14 | 43,26 | 43,27 | 43,28 | 43,29 | 43,32 | 43,33 | 43,34 | 43,35 | 43,37 |
| m | ||||||||||
| Х | 43,38 | 43,39 | 43,41 | 43,42 | 43,43 | 43,44 | 43,45 | 43,46 | 43,47 | 43,48 |
| m | ||||||||||
| Х | 43,49 | 43,50 | 43,51 | 43,52 | 43,53 | 43,54 | 43,55 | 43,57 | 43,58 | 43,59 |
| m | ||||||||||
| Х | 43,60 | 43,61 | 43,63 | 43,64 | 43,65 | 43,66 | 43,67 | 43,68 | 43,72 | 43,77 |
| m | ||||||||||
| Х | 43,78 | 43,82 | 43,94 | |||||||
| m |
1 Используя полученные данные, найдем значение среднего арифметического Х и оценки среднего квадратического отклонения Sх:
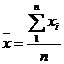

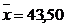
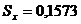
2.С помощью правила «трех сигм» проверяем наличие или отсутствие промахов.

Таким образом, ни один из результатов не выходит за границы интервала [ 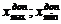 ], следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.
], следовательно, с вероятностью 0.9973 гипотеза об отсутствии грубых погрешностей принимается.
3.Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.
Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разобьем на k одинаковых интервалов 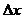 .
.

Принимая k=7, получим
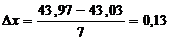
Т.к. в крайние интервалы попадает меньше 5 наблюдений, то объеденим их с соседними.
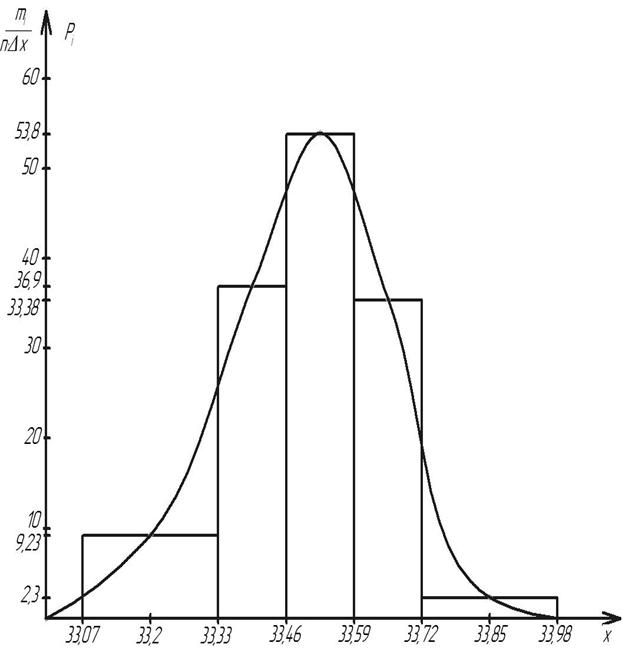
Результаты производимых вычислений занесем в первую половину таблицы 1, и строим гистограмму.
Из вида гистограммы можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.
| Xi-1 | Xi | m | 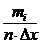
| 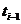
| 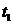
| Фi-1 | Фi | Pi | 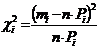
|
| 43,05 | 43,22 | 0.48 | -2.86 | -0.70 | -0.4979 | -0.2794 | 0.2341 | 2.660 | ||
| 43,22 | 43,26 | |||||||||
| 43,26 | 43,38 | |||||||||
| 43,38 | 43,51 | 2,92 | -0,76 | 0,06 | -0,2794 | 0,0239 | 0.2399 | 1,380 | ||
| 43,51 | 43,64 | 2,38 | 0,06 | 0,89 | 0,0239 | 0,3133 | 0,2894 | 0,035 | ||
| 43,64 | 43,77 | 0.6 | 0.89 | 2.80 | 0.3133 | 0.4974 | 0.1841 | 0.009 | ||
| 43,77 | 43,90 |
4.Проверка нормальности закона распределения по критерию Пирсона.
Т.к. в предыдущем пункте выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

В данном случае значения x1 и x2 соответствуют началу и концу интервала. Для каждого из значений нужно рассчитать относительный доверительный интервал  , а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t1) Ф(t2).
, а затем из таблиц функции Лапласа находим соответствующие значения этой функции Ф(t1) Ф(t2).
Найдя, таким образом, значения Pi для каждого интервала ki, заполним соответствующие ячейки таблицы, а затем рассчитаем значение c2 – критерия для каждого интервала.
Суммарное значение c2:4,084
Определим табличное (критическое) значение c2, задавшись доверительной вероятностью 0.97 и вычислив по формуле r=k-3 число степеней свободы:
r=5-3=2
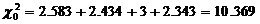
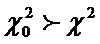
Таким образом, с вероятностью 0.97 гипотеза о нормальности распределения вероятности результата измерения принимается.
Представление результата в виде доверительного интервала.
Для этого определим стандартное отклонение среднего арифметического 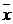 :
:
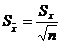 ;
;
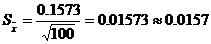
Т.к. закон распределения вероятности для среднего арифметического считаем нормальным, тогда доверительный интервал определится по выражению (значению доверительной вероятности 0.97 соответствует аргумент функции Лапласа t=0,99):
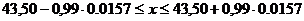

гистограмма
Список литературы
1.Методические указания по выполнению курсовых и контрольных работ по дисциплине «Метрология, стандартизация и сертификация» / Борискин О.Н., Соловьев С.Н., Белов Д.Б., Якушенков А.В.: Тул. Гос. Ун-т. Тула, 2004г.
2.Методические указания по выполнению курсовых и контрольных работ для студентов всех специальностей «Расчет сборочных размерных цепей методами взаимозаменяемости» / Маликов А.Б., Полукарова Е.Д.: Тула 1994г.
3. Приложение к методическим указаниям по выполнению курсовых и контрольных работ для студентов всех специальностей «Поля допусков и рекомендуемые посадки. ГОСТ 25347-82» / Тула 1994г.