Введение
Объектом исследования является листок бумаги.
Целью данной работы является косвенное измерение площади образца бумаги №23 прямоугольной формы посредством прямых измерений его линейных размеров (длины и ширины).
В задачи работы входит оценка погрешностей, случайных и систематических ошибок косвенных и прямых измерений.
Основная часть
Характеристика используемых в работе материалов и средств
Измерений
В работе использовались следующие материалы и средства измерений:
1. Лист бумаги (образец №23).
2. Линейка деревянная, диапазон измерения от 0 до 25 см, минимальная цена деления 1 мм (данных метрологической поверки нет).
3. Линейка металлическая, диапазон измерения от 0 до 25 см, минимальная цена деления 0,5 мм (данных метрологической поверки нет).
2 Описание методики проведения работы
Измеряем длину (a) образца листа бумаги №23 деревянной линейкой вдоль его продольных ребер в пяти разных местах (na = 5), ширину (b) - металлической линейкой вдоль поперечных ребер также в пяти разных местах (nb = 5). Так как возможно, что образец №23 не имеет строгой прямоугольной формы, то для уменьшения методической систематической ошибки определения его объема путем перемножения линейных размеров применим метод рандомизации и места измерений длины и ширины выберем по случайному принципу (в этом случае систематические ошибки в определении линейных размеров переходят в разряд случайных). Схема примерного расположения линий измерений длины и ширины приведена на рисунке 1.
Рисунок 1 – Линии измерений линейных размеров листа бумаги
Полученные результаты измерений в виде возрастающих вариационных рядов сводим в таблицу 1.
Таблица 1 - Результаты измерений линейных размеров образца бумаги
| Номер измерения (i) | Длина (ai), m | Ширина (bi), m |
| 0,128 | 0,0550 | |
| 0,128 | 0,0550 | |
| 0,128 | 0,0560 | |
| 0,128 | 0,0560 | |
| 0,128 | 0,0560 |
Обработка и анализ полученных в работе результатов
Так как в работе были проведены повторные измерения линейных размеров образца №23, то истинное значение его площади (S) примем равным среднему арифметическому значению, которое рассчитаем по формуле:
Из-за отсутствия сведений об исключаемых систематических ошибках для дальнейших расчетов воспользуемся неисправленными единичными значениями линейных размеров, приведенных в таблице.
В результатах измерения длины образца №23 не присутствуют разные значения и поэтому статистическую проверку на наличие грубых ошибок в данной выборке сделать возможно.
В результатах измерения ширины образца №23 присутствуют только два разных значения и поэтому статистическую проверку на наличие грубых ошибок в данной выборке сделать возможно.
Так как истинный закон распределения результатов измерений площади образца №23 неизвестен, то выберем следующую форму для представления конечных результатов измерения [1]:
` 
; 
, n; d` S,пр..
Выполним следующие расчеты:
м;
м;
м2.
Сделав допущение о нормальном законе распределения результатов измерения объема образца №23, можно рассчитать общую возможную предельную погрешность (П`S,пр.), предельную случайную (xслуч.,`S,пр.) и возможную предельную систематическую (xсист.,`V,пр.) ошибки измерения объема по формулам:
П` S,пр.= xслуч.,` S ,пр. + xсист.,` S ,пр. » S` S ×½tP,n½ + d` S,пр..
Так как найденное значение площади образца №23 по данной методике является результатом косвенного измерения, то используем следующие законы накопления ошибок.
Закон накопления случайных ошибок косвенных измерений:
=
= 
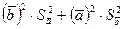=(0,0556)²*0+(0,128)²*0,104=0,0017039м²
Для определения возможной предельной случайной ошибки среднего арифметического значения площади образца№23 выполним следующие расчеты:
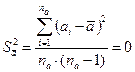м²;
м²;
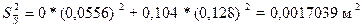
=0,0412783м²;
Принимая традиционную для дорожной отрасли вероятность событий (Р = 0,95) и объем выборки для определения площади образца №23 n = 5 (как наименьший из объемов выборки для линейных размеров), берем [2] табличное значение критерия Стьюдента ½tP,n½= 2,78 (число степеней свободы f = n-1=4)
Тогда,
xслуч.,` S ,пр. = S` s ×½tP,n½= 2,78*0,0412783=0,1147537м2.
Сделаем допущение, что общая остаточная систематическая ошибка измерения площади образца №23 определяется только систематической ошибкой средств измерения. Тогда, исходя из закона накопления относительных систематических ошибок:
= 0,001/0,128+ 0,0005/0,0556=
0,0078125+0,0089928=0,0168053;
0,0168053*0,0071168=0,0001196м²;
П` S,пр.= xслуч.,S,пр. + xсист.,`S,пр. » S` S ×½tP,n½ + d` S,пр.= 0,1147537 + 0,0001196 =
0,0000137 м2
» 2,36%
Заключение
В результате проведенной работы получены следующие результаты измерений объема ДСтП:
S = 0,007м2; S`S = 0,0413м2; n = 5; d` S,пр..= 0,001м2.
Результаты расчетов показали, что точность измерений является хорошей, так как общая возможная предельная относительная погрешность измерения площади образца №23 не превысила 5 %.
Список использованных источников
1.. Глебов И.Т., Глухих В.В., Назаров И.В. Научно-техническое творчество: Учеб. пособие. Екатеринбург: Урал. гос. лесотехн. ун-т, 2002. 264 с.
2. Основы научных исследований: Методические рекомендации и контрольные задания по дисциплине "Основы научных исследований" для самостоятельной работы студентов инженерно-экологического и заочного факультетов:В.В.Глухих, В.Г.Бурындин, Т.С.Выдрина, В.С.Таланкин, В.Б.Терентьев. Екатеринбург: Урал. гос. лесотехн. ун-т, 2007. 40 с.
Реферат
Отчет 6., 1 рис., 1 табл., 2 источника.
ЛИСТОК БУМАГИ, ЛИНЕЙКА, ИЗМЕРЕНИЕ ПЛОЩАДИ ЛИСТКА БУМАГИ
Объектом исследования является листок бумаги.
Целью данной работы является косвенное измерение площади образца бумаги №23 прямоугольной формы посредством прямых измерений его линейных размеров (длины и ширины).
В задачи работы входит оценка погрешностей, случайных и систематических ошибок косвенных и прямых измерений.
В результате проведенной работы получены следующие результаты измерений объема ДСтП:
S = 0,007м2; S`S = 0,0413м2; n = 5; d` S,пр..= 0,001м2.
Результаты расчетов показали, что точность измерений является хорошей, так как общая возможная предельная относительная погрешность измерения площади образца №23 не превысила 5 %.