►16. 2. Потребность сборочного предприятия в деталях некоторого типа составляет 120000 деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Хранение детали на складе стоит 0,35 ден. ед. в сутки, а поставка партии - 10000 ден. ед. Задержка производства из-за отсутствия деталей недопустима. Определить наиболее экономичный объем партии и интервал между поставками, которые нужно указать в заказе (предполагается, что поставщик не допускает задержки поставок).
Решение. По условию затраты на одну партию составляют c1 = 10000 ден. ед., затраты хранения единицы запаса в сутки c2 =0,35 ден. ед. Общий промежуток времени θ =1 год=365 дней, а общий объем запаса за этот период N = 120 000 деталей. По формуле (16.9)  дет., а по (16.14)
дет., а по (16.14) 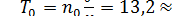 дней.
дней.
Итак, наиболее экономичный объем партии равен 4335 деталей, а интервал между поставками ≈ 13 дней.
На практике, естественно, объем партии может отличаться от оптимального n0, вычисленного по (9). Так, в предыдущей задаче может оказаться удобным заказывать партии по 4 500 или даже по 5 000 деталей и возникает вопрос, как при этом изменятся суммарные затраты.
Для ответа на этот вопрос разложим функцию С(n) в ряд Тейлора в окрестности точки n0, ограничившись первыми тремя членами ряда при достаточно малых изменениях объема партии ∆n:

Учитывая, что при n=n0 
 а C0=C(n0) определяется по формуле (12), найдем:
а C0=C(n0) определяется по формуле (12), найдем:

или
 (16)
(16)
Формула (16) свидетельствует об определенной устойчивости суммарных затрат по отношению к наиболее экономичному объему партии, ибо при малых ∆n относительное изменение затрат примерно на порядок меньше относительного изменения объема партии по сравнению с оптимальным.
► 16.3. По условию задачи 16.2 определить, на сколько процентов увеличатся затраты на создание и хранение запаса по сравнению с минимальными затратами при объеме заказываемых партий 5000 деталей.
Решение. Относительное изменение объема партии по сравнению с оптимальным n0 = 4335 составляет ∆n/n0 = (5000 - 4335)/4335=0,153. В соответствии с (16) относительное изменение суммарных затрат составит ∆С/С0 = 0,1532/2 ≈ 0,012, или лишь 1,2%.
► 16.4. В условиях задачи 16.3 предположим, что заказываются не все партии сразу, а каждая отдельно, причем срок выполнения заказа равен 16 дней. Определить точки заказа, т.е. при каком уровне запаса следует заказывать следующую партию.
Решение. Так как по результатам решения задачи 16.2 длина интервала между поставками равна 13,2 дней, то заказ в условиях налаженного производства следует возобновить, когда уровень запаса достаточен для удовлетворения потребности на 16 - 13,2=2,8 дня. Так как ежедневная потребность (интенсивность расхода запаса) равна по формуле (3) b=120 000/365=329 деталей, то заказы должны делаться регулярно при достижении уровня запаса 329*2,8 ≈922 деталей.►
Статическая детерминированная модель с дефицитом
В рассматриваемой модели будем полагать наличие дефицита. Это означает, что при отсутствии запасаемого продукта, т.е. при J(t) = 0 спрос сохраняется с той же интенсивностью  , но потребление запаса отсутствует - b(t) = 0, вследствие чего накапливается дефицит со скоростью b. График изменения уровня запаса в этом случае представлен на рис.3. Убывание графика ниже оси абсцисс в область отрицательных значений в отличие от графика на рис.2 характеризирует накопление дефицита.
, но потребление запаса отсутствует - b(t) = 0, вследствие чего накапливается дефицит со скоростью b. График изменения уровня запаса в этом случае представлен на рис.3. Убывание графика ниже оси абсцисс в область отрицательных значений в отличие от графика на рис.2 характеризирует накопление дефицита.
Из рис.3 видно, что каждый период «пилы»  разбивается на два временных интервала, т.е. T=T1+T2, где T1 – время, в течение которого производится потребление запаса, T2 – время, когда запас отсутствует и накапливается дефицит, который будет перекрыт в момент поступления следующей партии.
разбивается на два временных интервала, т.е. T=T1+T2, где T1 – время, в течение которого производится потребление запаса, T2 – время, когда запас отсутствует и накапливается дефицит, который будет перекрыт в момент поступления следующей партии.

Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса s в момент поступления каждой партии теперь не равен ее объему n, а меньше его на величину дефицита n-s, накопившегося за время Т2 (рис. 3).
Из геометрических соображений легко установить, что
 (17)
(17)
В данной модели в функцию суммарных затрат С наряду с затратами С1 (на пополнение запаса) и С2 (на хранение запаса) необходимо ввести затраты Сз - на штраф из-за дефицита, т.е. C=C1+C2+C3 .
Затраты С1, как и ранее, находим по формуле (11). Затраты С2 при линейном расходе запаса равны затратам на хранение среднего запаса, который за время потребления Т1 равен sT1/2; поэтому с учетом (7) и (5) эти затраты составят
 =
=  (18)
(18)
При расчете затрат С3 будем считать, что штраф за дефицит составляет в единицу времени с3 на каждую единицу продукта. Так как средний уровень дефицита за период Т2 равен (n- s) T2/2,то штраф за этот период Т2 составит  с3(n-s)T2, а за весь период θ с учетом (7) и (19)
с3(n-s)T2, а за весь период θ с учетом (7) и (19)
 (19)
(19)
Теперь, учитывая (12), (18) и (19), суммарные затраты равны
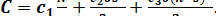 (20)
(20)
Нетрудно заметить, что при n=s формула (19) совпадает с ранее полученной (8) в модели без дефицита.
Рассматриваемая задача управления запасами сводится к отысканию такого объема партии n и максимального уровня запаса s, при которых функция С (9) принимает минимальное значение. Другими словами, необходимо исследовать функцию двух переменных С (n,s) на экстремум. Приравнивая частные производные ∂C/∂n, ∂C/∂s к нулю, получим после преобразований систему уравнений:
 (21)
(21)
Решая систему, получаем формулы наиболее экономичного объема партии ñ0 и максимального уровня запаса s̃0 для модели с дефицитом:
 (22)
(22)
 (23)
(23)
Величина 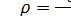 (24)
(24)
называется плотностью убытков из-за неудовлетворенного спроса и играет важную роль в управлении запасами. Заметим, что 0≤ρ≤1. Если значение с3 мало по сравнению с с2, то величина ρ близка к нулю: когда с3 значительно превосходит с2,то ρ близка к 1. Недопустимость дефицита равносильна предположению, что с3 = ∞ или ρ = 1.
Используя (24), основные формулы (22) и (23) можно записать компактнее:
 (25)
(25)
 (26)
(26)
В силу (17) и (26) T1/T = s̃0/n  0= ρ и Т2/Т= (n
0= ρ и Т2/Т= (n  0 - s̃0 )/ n
0 - s̃0 )/ n  0 = 1-ρ. Поэтому утверждение о том, что плотность убытков из-за неудовлетворенного спроса равна ρ, означает, что в течение (1- ρ) 100% времени от полного периода T запас продукта будет отсутствовать.
0 = 1-ρ. Поэтому утверждение о том, что плотность убытков из-за неудовлетворенного спроса равна ρ, означает, что в течение (1- ρ) 100% времени от полного периода T запас продукта будет отсутствовать.
Из сравнения формул (25) и (10) следует, что оптимальные объемы партий для задач с дефицитом и без дефицита при одинаковых параметрах связаны соотношением
 (27)
(27)
откуда вытекает, что оптимальный объем партии в задаче с дефицитом всегда больше (в 1/  раз), чем в задаче без дефицита.
раз), чем в задаче без дефицита.
► 16.5. Найти наиболее экономичный объем партии и интервал между поставками, сохраняя условия задачи 16.2, кроме недопустимости дефицита, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере 3,5 ден. ед.
Решение. По условию с3 = 3,5. Ранее было получено по формуле (9) n0 =4335 и по (15) Т0 =13,2. Найдем плотность убытков из-за неудовлетворенного спроса по формуле (24): ρ=3,5/(0,35 + 3,5)=0,909, т.е. 100(1-0,909)=9,1% времени между поставками детали на сборке будут отсутствовать.
Теперь оптимальный размер партии по формуле (27) ñ0 = 4335/  = 4547. В силу (15) пропорционально увеличению ñ0 должен увеличиться интервал между поставками, т.е. T̃0 = T0/
= 4547. В силу (15) пропорционально увеличению ñ0 должен увеличиться интервал между поставками, т.е. T̃0 = T0/  = 13,2/
= 13,2/  = 13,8 ≈14 дней.
= 13,8 ≈14 дней.
Стохастические модели управления запасами
Рассмотрим стохастические модели управления запасами, у которых спрос является случайным. Этот факт существенным образом сказывается на характере соответствующих моделей и значительно усложняет их анализ, в связи с чем в рамках данной книги ограничимся рассмотрением наиболее простых моделей.
Предположим, что спрос r за интервал времени Т является случайным и задан его закон (ряд) распределения р(r) или плотность вероятностей φ(r) (обычно функции р(r) и φ(r) оцениваются на основании опытных или статистических данных). Если спрос r ниже уровня запаса s, то приобретение (хранение, продажа) излишка продукта требует дополнительных затрат c2 на единицу продукта; наоборот, если спрос r выше уровня запаса s, то это приводит к штрафу за дефицит с3 на единицу продукции.
В качестве функции суммарных затрат, являющейся в стохастических моделях случайной величиной, рассматривают ее среднее значение или математическое ожидание.
В рассматриваемой модели при дискретном случайном спросе r, имеющем закон распределения р(r), математическое ожидание суммарных затрат имеет вид:
 (28)
(28)
В выражении (28) первое слагаемое учитывает затраты на приобретение (хранение) излишка s-r единиц продукта (при r≤s), а второе слагаемое - штраф за дефицит на r-s единиц продукта (при r> s).
В случае непрерывного случайного спроса, задаваемого плотностью вероятностей φ(r), выражение C(s) принимает вид:
 (29)
(29)
Задача управления запасами состоит в отыскании такого запаса s, при котором математическое ожидание суммарных затрат (28) или (29) принимает минимальное значение.
Доказано, что при дискретном случайном спросе r выражение (28) минимально при запасе s0, удовлетворяющем неравенствам
 (30)
(30)
а при непрерывном случайном спросе r выражение (29) минимально при значении s0, определяемом из уравнения
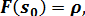 (31)
(31)
где
 (32)
(32)
есть функция распределения спроса r,F(s0) и F(s0+1) - ее значения; ρ - плотность убытков из-за неудовлетворенного спроса, определяемая по (24).
Оптимальный запас s0 при непрерывном спросе по данному значению ρ может быть найден и графически (рис. 4).
 |
► 16.6. Предприятие закупает агрегат с запасными блоками к нему. Стоимость одного блока равна 5 ден. ед. В случае выхода агрегата из строя из-за поломки блока, отсутствующего в запасе, простой агрегата и срочный заказ нового блока к нему обойдется в 100 ден. ед. Опытное распределение агрегатов по числу блоков, потребовавших замену, представлено в табл. 1.
Таблица 1
| Число замененных блоков r | |||||||
| Статистическая вероятность | |||||||
| (доля) агрегатов р(r), которым | 0,90 | 0,05 | 0,02 | 0,01 | 0,01 | 0,01 | 0,00 |
| потребовалась замена r блоков |
Необходимо определить оптимальное число запасных блоков, которое следует приобрести вместе с агрегатом.
Решение. По условию с2 = 5, с3 = 100. Вычислим плотность убытков из-за нехватки запасных блоков по формуле (24) ρ = 100/(5+100) = 0,952.
Учитывая (32), найдем значения функции распределения спроса (таб. 2).
Таблица 2
| s | >6 | |||||||
| r | >6 | |||||||
| F(s) | 0,00 | 0,00 | 0,90 | 0,95 | 0,97 | 0,98 | 0,99 | 1,00 |
Очевидно (таб. 2), что оптимальный запас составит s0=3, ибо он удовлетворяет неравенству (30): F(3) < 0,952 < F(4). ►
►16 .7. Решить задачу 16.6 при условии непрерывного случайного спроса r, распределенного по показательному закону с функцией распределения F(r) = 1 - е-λr при λ = 0,98.
Решение. Оптимальное число запасных блоков s0 найдем из уравнения (31):  откуда
откуда  и
и  При λ = 0,98 s0 = - (1/0,98) ln 0,02 ≈ 4 (блока).
При λ = 0,98 s0 = - (1/0,98) ln 0,02 ≈ 4 (блока).
В условиях рассматриваемой модели предположим, что расходование запаса происходит непрерывно с одинаковой интенсивностью. Такую ситуацию можно представить графически (рис. 5).
 Рис.5
Рис.5
Рис. 5, а соответствует случаю r ≤ s, когда спрос не превосходит запаса, а рис. 5, б - случаю, когда спрос превышает запас, т.е. r> s. Следует отметить, что на самом деле график J(t) представляет ступенчатую ломаную, показанную на рис. 5 пунктиром, но для исследования модели нам проще рассматривать J(t) в виде прямой, сглаживающей эту ломаную.
Средний запас, соответствующий рис. 5, а, равен
 (33)
(33)
Средний запас, соответствующий рис. 6, б с учетом формулы (17), в которой полагаем n = r, составляет
 (34)
(34)
Средний дефицит продукта за период T2 для случая, соответствующего рис. 5, б с учетом (17), где n = r, равен
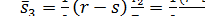 (35)
(35)
Математическое ожидание суммарных затрат составит:
 (36)
(36)
Доказано, что в этом случае математическое ожидание (36) минимально при запасе s0, удовлетворяющем неравенству
L (s0) < ρ < L (s0 + 1), (37)
где ρ по-прежнему определяется по формуле (24):
 (38)
(38)
L(s0) и L(s0+1) - значения функции (38), a F(s) находится в соответствии с определением (32).
►16.8. Имеющиеся на складе изделия равномерно расходуются в течение месяца. Затраты на хранение одного изделия, составляют 5 ден. ед., а штраф за дефицит одного изделия обходится в 100 ден. ед. Изучение спроса дало распределение числа потребляемых за месяц изделий (таб. 3).
Таблица 3
| Спрос r | ≥6 | ||||||
| Статистическая | |||||||
| вероятность р(r) | 0.1 | 0.2 | 0,2 | 0,3 | 0,1 | 0,1 | 0,0 |
Необходимо, определить оптимальный месячный запас склада.
Решение. Так же как в задаче 16.6, c2 = 5, с3 = 100, ρ= 0,952.
Значения функции L(r) определим с помощью табл. 4.
Таблица 4
| s | r | p(r) | 
| 
| 
| F(r) | L(r) |
| 0,1 | — | — | — | 0,0 | — | ||
| 0,2 | 0,200 | 0,445 | 0,2225 | од | 0,3225 | ||
| 0,2 | 0,100 | 0,245 | 0,3675 | 0,3 | 0,6675 | ||
| 0,3 | 0,100 | 0,145 | 0,3625 | 0,5 | 0,8625 | ||
| 0,1 | 0,025 | 0,045 | 0,1575 | 0,8 | 0,9575 | ||
| 0,1 | 0,020 | 0,020 | 0,0900 | 0,9 | 0,9900 | ||
| ≥6 | ≥6 | 0,0 | 0,000 | 0,000 | 0,0000 | 1,0 | 1,0000 |
Очевидно, что оптимальный запас изделий s0 = 3, ибо он удовлетворяет условию (37): L(3) < 0,952 < L(4).