НУЛЕВОЙ ВАРИАНТ
Примечание. Дробный ответ представляется неправильной несократимой дробью 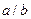 .
.
| №п/п | Задания | Ответы | ||||||||||
| Раздел: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ. | ||||||||||||
| Тема 10.1: ДУ первого порядка-1. Тема 10.2: ДУ первого порядка-2. Дифференциальное уравнение с разделяющимися переменными, однородное ДУ, линейное ДУ,уравнение Бернулли,нахождение их общих и частных решений. | ||||||||||||
Общий интеграл дифференциального уравнения  имеет вид:
1) имеет вид:
1) 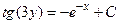 2) 2) 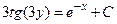 3) 3) 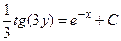 4) 4)  5) 5) 
| 4) | |||||||||||
| 2. | Дано дифференциальное уравнение  . Тогда функция . Тогда функция  является его решением при является его решением при 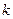 равном:
1) равном:
1) 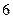 2) 2) 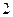 3) 3) 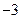 4) 4) 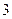 5) 5) 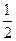
| 1) | ||||||||||
| 3. | Общий интеграл дифференциального уравнения 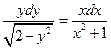 имеет вид:
1) имеет вид:
1)  2) 2)  3) 3) 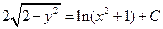 4)
4) 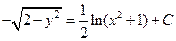 5) 5) 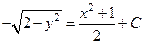
| 4) | ||||||||||
| 4. | Общее решение дифференциального уравнения  имеет вид:
1) имеет вид:
1) 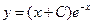 2) 2) 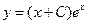 3) 3) 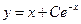 4) 4) 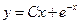
| 1) | ||||||||||
| 5. | Частное решение дифференциального уравнения  при при 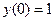 имеет вид:
1) имеет вид:
1) 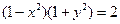 2) 2)  3) 3)  4) 4) 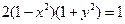
| 1) | ||||||||||
| 6. | Из перечисленных ниже функций общим решением дифференциального уравнения 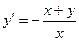 является:
1) является:
1) 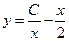 2) 2) 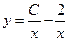 3) 3)  4) 4) 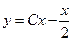 5) 5) 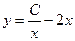
| 1) | ||||||||||
| 7. | Дана задача Коши: 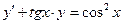 , , 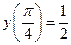 . Тогда значение . Тогда значение  её решения её решения  равно…
Записать ответ. равно…
Записать ответ.
| |||||||||||
Тема 10.3: ДУ высших порядков-1.
Тема 10.4: ДУ высших порядков-2.
ДУ допускающие понижение порядка, линейные однородные и неоднородные ДУ с постоянными коэффициентами и правой частью специального вида, нахождение их общих и частных решений. Нахождение общих и частных решений дифференциальных уравнений вида: 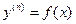 ; ;  ; ; 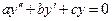 ; ;  . Нахождение корней характеристических уравнений. . Нахождение корней характеристических уравнений.
| ||||||||||||
| 1. | Дана задача Коши: 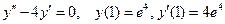 . Тогда значение . Тогда значение  её решения её решения  равно…
Записать ответ. равно…
Записать ответ.
| |||||||||||
| 2. | Соответствие дифференциального уравнения его общему решению:
1: 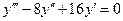 1: 1: 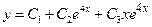 2:
2: 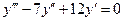 2: 2: 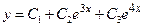 3:
3: 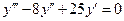 3: 3: 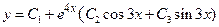 В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
В ответе указать пары, соответствующих друг другу ДУ и их общих решений.
| 1-1 2-2 3-3 | ||||||||||
| 3. | Соответствие дифференциального уравнения корням его характеристического уравнения:
1: 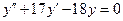 1: 1: 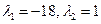 2:
2: 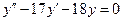 2: 2: 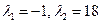 3:
3: 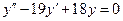 3: 3:  В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
В ответе указать пары, соответствующих друг другу ДУ и корней их характеристических уравнений.
| 1-1 2-2 3-3 | ||||||||||
| 4. | Общим решением дифференциального уравнения 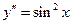 является функция:
1) является функция:
1)  2) 2)  3) 3) 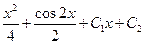 4)
4)  5) 5) 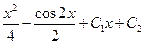
| 4) | ||||||||||
| 5. | Общее решение дифференциального уравнения 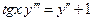 имеет вид имеет вид  , где , где  ( (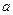 - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 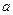
| -2 | ||||||||||
| 6. | Частное решение 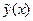 неоднородного линейного дифференциального уравнения неоднородного линейного дифференциального уравнения 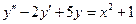 имеет вид имеет вид  , где , где  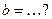 ( (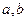 - целые числа).
Ответ записать в виде: - целые числа).
Ответ записать в виде: 
| 4,23 | ||||||||||
| 7. | Частное решение 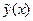 неоднородного линейного дифференциального уравнения неоднородного линейного дифференциального уравнения  представимо в виде:
1) представимо в виде:
1)  2)
2) 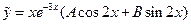 3)
3) 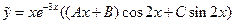 4)
4) 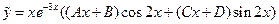 5)
5) 
| 4) | ||||||||||
| 8. | Частное решение дифференциального уравнения  при начальных условиях: при начальных условиях: 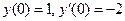 имеет вид:
1) имеет вид:
1) 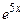 2) 2) 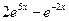 3) 3)  4) 4) 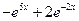 5) 5) 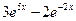
| 3) | ||||||||||
| 9. | Частное решение 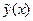 неоднородного линейного дифференциального уравнения неоднородного линейного дифференциального уравнения 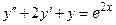 имеет вид имеет вид 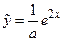 ,где ,где  ( (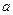 - целое число).
Ответ записать в виде: - целое число).
Ответ записать в виде: 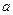
| |||||||||||
| 10. | Общее решение дифференциального уравнения 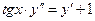 имеет вид:
1) имеет вид:
1) 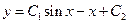 2) 2) 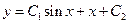 3) 3) 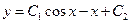 4)
4)  5) 5) 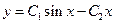
| 1) | ||||||||||
Тема 10.5: ДУ (теория-1):Определение порядка дифференциального уравнения. Определение типа дифференциального уравнения первого порядка (ДУ с разделяющимися переменными; однородное; линейное; Бернулли). Определение типа дифференциального уравнения высшего порядка (простейшее (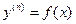 ); допускающее понижение порядка ( ); допускающее понижение порядка ( , , 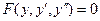 ); линейное). ); линейное).
| ||||||||||||
| 1. | Соответствие дифференциального уравнения его названию:
1:  1: линейное
2: 1: линейное
2: 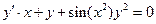 2: Бернулли
3: 2: Бернулли
3:  3: однородное
4: 3: однородное
4: 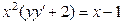 4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий. 4: с разделяющимися переменными
В ответе указать пары, соответствующих друг другу ДУ и их названий.
| 1-1 2-2 3-3 4-4 | ||||||||||
| 2. | Порядок дифференциального уравнения 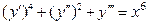 равен…
Записать ответ. равен…
Записать ответ.
| |||||||||||
| 3. | Из ниже перечисленных дифференциальных уравнений высшего порядка понижение порядка допускают уравнения:
1)  2) 2) 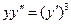 3) 3)  4)
4) 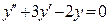 5) 5) 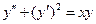 Указать все правильные ответы.
Указать все правильные ответы.
| 1)2)4) | ||||||||||
| Раздел: ТЕОРИЯ ВЕРОЯТНОСТЕЙ. | ||||||||||||
Тема 11.1: Комбинаторика:Правила суммы и произведения комбинаторики; комбинаторные числа  , ,  , ,  , подсчёт их числа. , подсчёт их числа.
| ||||||||||||
| 1. | Количество различных трёхзначных чисел не делящихся на 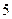 равно:
1) равно:
1)  2) 2)  3) 3) 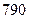 4) 4)  5) 5) 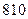
| 1) | ||||||||||
| 2. | В новогоднем шахматном турнире участвуют 10 человек. Между любыми двумя участниками турнира должна быть сыграна одна партия. Тогда общее число партий, которое должно быть сыграно в турнире, равно:
1) 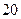 2) 2)  3) 3) 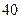 4) 4) 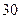 5) 5) 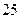
| 2) | ||||||||||
| 3. | Соответствие комбинаторного числа его значению:
1: 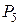 1: 1:  2:
2: 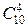 2: 2:  3:
3: 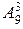 3: 3:  В ответе указать пары, соответствующих друг другу комбинаторных чисел и их значений.
В ответе указать пары, соответствующих друг другу комбинаторных чисел и их значений.
| 1-1 2-2 3-3 | ||||||||||
| 4. | В урне 5 чёрных и 6 белых шаров. Наудачу вынимают 4 шара. Тогда число способов отбора, при котором среди четырёх выбранных окажется два белыхшара, равно:
1)  2) 2) 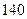 3) 3) 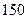 4) 4) 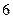 5) 5) 
| 3) | ||||||||||
| Тема 11.2: Случайные события-1:Классическое определение. | ||||||||||||
| 1. | Наудачу выбрано двузначное число. Тогда вероятность того, что выбранное число простое (делится нацело только на единицу и на себя) и сумма его цифр – пять, равна:
1) 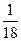 2) 2) 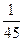 3) 3) 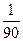 4) 4) 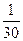 5) 5) 
| 2) | ||||||||||
| 2. | Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани кости появится менее трёх очков, равна:
1)  2) 2) 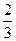 3) 3)  4) 4)  5) 5) 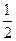
| 3) | ||||||||||
| 3. | Бросают три монеты. Тогда вероятность того, что «герб» появится хотя бы на одноймонете, равна:
1)  2) 2)  3) 3) 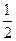 4) 4) 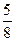 5) 5) 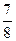
| 5) | ||||||||||
| 4. | В урне двабелых, три чёрных и пять красных шаров. Наудачу вынимают тришара. Тогда вероятность того, что все вынутые шары одного цвета, равна 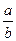 , где , где  , , 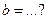 ( (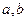 - целые числа).
Ответ представить в виде несократимой дроби: - целые числа).
Ответ представить в виде несократимой дроби: 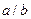
| 11/120 | ||||||||||
| Тема 11.3: Случайные события-2: Тема 11.4: Случайные события-3: Классическое определение, формулы сложения и умножения (открытая форма).Формула Бернулли, формулы полной вероятности и Байеса. | ||||||||||||
| 1. | Среди кандидатов в студсовет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу в студсовет выбирают 5 человек. Тогда вероятность того, что среди выбранных окажутся все три первокурсника, равна 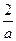 , где , где  ( (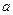 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 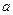
| |||||||||||
| 2. | Учитель каждый день случайным образом отбирает одного ученика для проверки подготовки домашнего задания. Известно, что из 18 учеников 12 всегда полностью выполняют домашнее задание. Тогда вероятность того, что за шесть дней недели учитель выставит четыре отрицательныеоценки равна  , где , где  ( (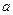 - целое число).
Ответ представить в виде: - целое число).
Ответ представить в виде: 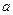
| |||||||||||
| 3. | Три станка-автомата производят однотипную продукцию, поступающую на сборочное производство в пропорции 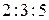 . Известно, что средний процент бракадля первого станка равен 2%, для второго – 3% и для третьего – 1%. Выбранная наудачу деталь оказаласьбракованной. Тогда вероятность того, что данная деталь изготовлена на втором станке, равна . Известно, что средний процент бракадля первого станка равен 2%, для второго – 3% и для третьего – 1%. Выбранная наудачу деталь оказаласьбракованной. Тогда вероятность того, что данная деталь изготовлена на втором станке, равна 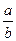 , где , где  , , 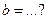 ( (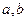 - целые числа).
Ответ представить в виде несократимой дроби: - целые числа).
Ответ представить в виде несократимой дроби: 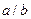
| 1/2 | ||||||||||
| 4. | В ящике лежало три лотерейных билета, из них один выигрышный. Один билет (неизвестно какой) был утерян. Тогда вероятность того, что билет, выбранный наудачу из оставшихся билетов, окажется выигрышным равна 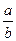 , где , где  , , 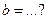 ( (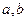 - целые числа).
Ответ представить в виде несократимой дроби: - целые числа).
Ответ представить в виде несократимой дроби: 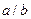
| 1/3 | ||||||||||
| 5. | Имеются три одинаковых по виду ящика. В первом ящике находятся 4 белых и 5 чёрных шаров, во втором – 5 белых и 4 чёрных, в третьем – 6 белых шаров. Из наудачу выбранного ящика вынули белый шар. Тогда вероятность того, что он вынут из второго ящика, равна  , где , где  ( (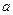 - целое число).
Ответ представить в виде: - целое число).
Ответ представить в виде: 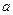
| |||||||||||
| 6. | Результаты проверки выполнения контрольной работы по ТВ в двух студенческих группах показали, что в первой группе положительную оценку получили 20 студентов из 30, а во второй группе – 15 из 25. Наудачу выбранная работа имеет оценку «неудовлетворительно». Тогда вероятность того, что она написана студентом первой группы, равна:
1) 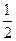 2) 2)  3) 3) 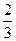 4) 4)  5) 5) 
| 1) | ||||||||||
| 7. | Вероятность выиграть в шахматы у равносильного противника хотя бы одну из четырёх партий (ничьи во внимание не принимаются) равна:
1)  2) 2) 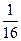 3) 3) 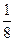 4) 4)  5) 5) 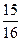
| 5) | ||||||||||
| 8. | Игральную кость бросают 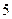 раз. Тогда вероятность того, что при этом число очков меньшее 5 появится менее двух или более четырёх раз, равна:
1) раз. Тогда вероятность того, что при этом число очков меньшее 5 появится менее двух или более четырёх раз, равна:
1)  2) 2) 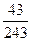 3) 3) 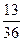 4) 4) 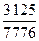 5) 5) 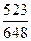
| 2) | ||||||||||
Вероятность попадания в цель при одном выстреле 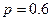 . Произведено три выстрела. Тогда вероятность того, что при этом будет иметь место хотя бы одно попаданиев цель, равна . Произведено три выстрела. Тогда вероятность того, что при этом будет иметь место хотя бы одно попаданиев цель, равна 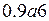 , где , где  ( (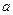 - цифра).
Ответ представить в виде: - цифра).
Ответ представить в виде: 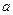
| ||||||||||||
Тема 11.5. Дискретные случайные величины-1.
Тема 11.6. Непрерывные случайные величины-1.
Тема 11.7. Случайные величины-2.
Ряд распределения дискретной случайной величины. Функции распределения 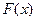 и плотности распределения и плотности распределения  непрерывной случайной величины, их взаимосвязь и свойства. Математическое ожидание и дисперсия дискретной и непрерывной случайных величин, их свойства и вычисление. непрерывной случайной величины, их взаимосвязь и свойства. Математическое ожидание и дисперсия дискретной и непрерывной случайных величин, их свойства и вычисление.
| ||||||||||||
| 1. | Известны дисперсии независимых случайных величин  и и 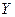 : : 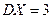 , , 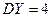 . Тогда дисперсия . Тогда дисперсия  случайной величины случайной величины  равна:
1) равна:
1) 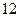 2) 2)  3) 3) 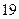 4) 4)  5) 5) 
| 2) | ||||||||||
| 2. | Известны математические ожидания случайных величин  и и 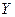 : : 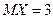 , , 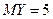 . Тогда математическое ожидание . Тогда математическое ожидание 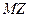 случайной величины случайной величины  равно…
Записать ответ. равно…
Записать ответ.
| -7 | ||||||||||
| 3. | Дискретная случайная величина  распределена по закону, заданному таблицей распределена по закону, заданному таблицей  . Известно, что её дисперсия . Известно, что её дисперсия 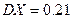 . Тогда вероятности . Тогда вероятности 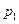 и и   равны:
1) равны:
1) 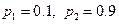 2) 2)  3) 3) 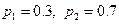 4)
4) 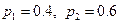 5) 5) 
| 3) | ||||||||||
| 4. | В партии из 6 деталей содержится 4 стандартных. Дискретная случайная величина  - число стандартных деталей среди трёх отобранных. Тогда её математическое ожидание - число стандартных деталей среди трёх отобранных. Тогда её математическое ожидание 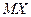 равно равно 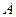 , где , где 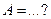 ( (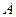 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 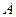
| |||||||||||
| 5. | Функция распределения непрерывной случайной величины  имеет вид имеет вид 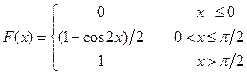 . Тогда её математическое ожидание . Тогда её математическое ожидание 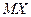 равно равно 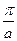 , где , где  ( (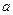 - целое число).
Ответ представить в виде: - целое число).
Ответ представить в виде: 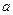
| |||||||||||
| Тема 11.9. Случайные величины-3:Основные законы распределения: биномиальный, равномерный, нормальный, показательный, их числовые характеристики. | ||||||||||||
| 1. | Случайная величина  имеет нормальный закон распределения, заданный функцией плотности имеет нормальный закон распределения, заданный функцией плотности 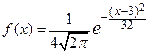 . Тогда дисперсия . Тогда дисперсия 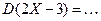 Записать ответ.
Записать ответ.
| |||||||||||
| 2. | Непрерывная случайная величина равномерно распределена на отрезке  . Тогда вероятность . Тогда вероятность 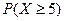 равна равна 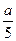 , где , где  ( (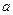 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 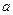
| |||||||||||
| 3. | Вероятность того, что при трёх выстрелах стрелок попадёт в цель хотя бы один раз, равна 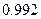 . Дискретная случайная величина . Дискретная случайная величина  - число попаданий в цель при 20 выстрелах, имеет биномиальное распределение. Тогда её дисперсия - число попаданий в цель при 20 выстрелах, имеет биномиальное распределение. Тогда её дисперсия 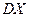 равна равна 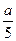 , где , где  ( (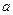 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 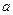
| |||||||||||
| 4. | Случайная величина  имеет показательный закон распределения, заданный функцией плотности имеет показательный закон распределения, заданный функцией плотности 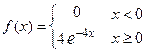 . Тогда дисперсия . Тогда дисперсия 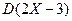 равна равна 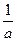 , где , где  ( (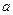 - целое число).
Вычисления проводить в дробях. Ответ представить в виде: - целое число).
Вычисления проводить в дробях. Ответ представить в виде: 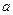
| |||||||||||
| Тема 12.1. Описательная статистика-1:Числовые характеристики выборки (среднее арифметическое, дисперсия, мода, медиана); графическое изображение выборки (полигон, гистограмма). | ||||||||||||
При измерении скорости ветра 26 сентября в течение 6 лет были получены значения:   . Тогда значение оценки средней скорости ветра 26 сентября равно:
1) . Тогда значение оценки средней скорости ветра 26 сентября равно:
1)  2) 2)  3) 3) 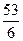 4) 4) 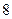 5) 5) 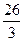
| 2) | |||||||||||
Дано статистическое распределение выборки объёма  : :
Тогда среднее арифметическое выборки | 1) 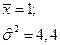
| |||||||||||
Дана выборка объёма  Тогда мода выборки Тогда мода выборки 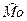 и медиана выборки и медиана выборки 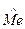 равны:
1) равны:
1)  2) 2) 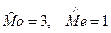 3) 3)  4) 4) 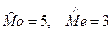
| 1) 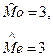
| |||||||||||
По выборке объема n=100 построена гистограмма частот:  Тогда значение а равно:
1)
Тогда значение а равно:
1) 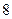 2) 2)  3) 3)  4) 4)  5) 5) 
| 1) | |||||||||||
Из генеральной совокупности извлечена выборка объёма  , полигон частот которой имеет вид: , полигон частот которой имеет вид:
 Тогда число вариант
Тогда число вариант  в выборке равно…
Записать ответ. в выборке равно…
Записать ответ.
| 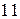
| |||||||||||
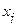

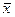 и дисперсия выборки
и дисперсия выборки 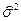 равны:
равны: