Вопрос №1. ЧМ решения задачи на собственные значения и собственные векторы матриц
Постановка задачи. Пусть дана невырожденная квадратная матрица  . Требуется найти её собственные значения
. Требуется найти её собственные значения 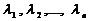 и собственные вектора.
и собственные вектора.
Определение. Вектор  , удовлетворяющий уравнению
, удовлетворяющий уравнению 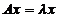 , называется собственным вектором (СВ) матрицы
, называется собственным вектором (СВ) матрицы 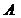 . Число
. Число 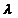 называется собственным значением (СЗ). Совокупность собственных значений оператора образует его спектр. Собственное значение и соответствующий собственный вектор образуют собственную пару
называется собственным значением (СЗ). Совокупность собственных значений оператора образует его спектр. Собственное значение и соответствующий собственный вектор образуют собственную пару 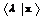 .
.
Свойства СЗ и СВ матрицы
1) Собственные вектора определяются с точностью до множителя: если 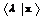 – собственная пара, то для любой неравной нулю константы
– собственная пара, то для любой неравной нулю константы 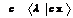 – тоже является собственной парой.
– тоже является собственной парой.
2) Если 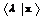 – собственная пара оператора
– собственная пара оператора 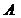 , то
, то 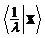 – собственная пара оператора
– собственная пара оператора  .
.
3) Если 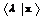 – собственная пара оператора
– собственная пара оператора 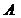 , то
, то 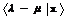 – собственная пара оператора
– собственная пара оператора  .
.
4) Спектр диагональных и треугольных матриц состоит из диагональных элементов этих матриц.
5) Определитель матрицы равен произведению ее собственных значений.
6) Собственные вектора, соответствующие различным собственным значениям линейно независимы. Кратному собственному значению соответствует от 1 до k линейно независимых собственных векторов. Если матрица имеет полный набор различных собственных значений, то собственные векторы образуют в пространстве базис, в котором матрица оператора имеет диагональный вид.
Определение. 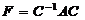 с невырожденной матрицей С называется преобразованием подобия, а матрицы F и A называются подобными. Преобразование подобия не изменяет собственных значений матрицы.
с невырожденной матрицей С называется преобразованием подобия, а матрицы F и A называются подобными. Преобразование подобия не изменяет собственных значений матрицы.
Из определения следует, что для определения собственного вектора необходимо найти нетривиальные решения однородного уравнения:
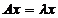
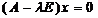


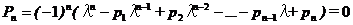 - характеристическое уравнение
- характеристическое уравнение
где 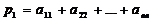 - след матрицы
- след матрицы

То есть задача нахождения собственных значений матрицы сводится к нахождению корней характеристического уравнения.
 | |||||
 |  | ||||
Различают полную и частичную (неполную) проблемы решения задачи. В полной определяют все СЗ и соответствующие им СВ. К методам, решающим полную проблему, относятся: метод Данилевского, метод вращений Якоби, метод LU-алгоритма. В неполной находят некоторые СЗ и соответствующие им СВ. К методам, решающим неполную проблему, относятся: степенной метод, обратно степенной метод.
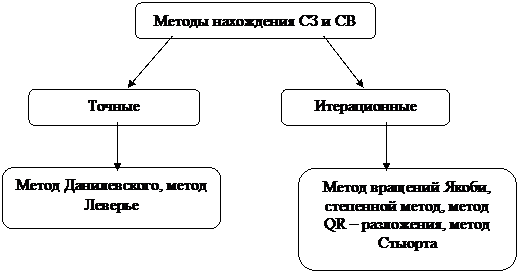 |
Методы нахождения СЗ и СВ бывают точные (прямые) и итерационные. В прямых методах, как правило, строят характеристическое уравнение и, решая его каким-либо известным методом, находят СЗ и по найденным собственным числам находят СВ. Итерационные вычисления носят итерационный характер, не строят характеристическое уравнение, и СЗ находят вместе с СВ. Точные методы решают полную проблему собственных значений. Итерационные методы могут решать как полную, так и частичную проблемы.
Точные методы: метод Данилевского, метод Леверье
Итерационные методы: метод вращений Якоби, степенной метод, метод QR – разложения, метод Стьюрта(Для вычисления группы собственных значений применяются так наз. методы одновременных итераций. Они представляют собой обобщение степенного метода, где вместо итераций одного вектора фактически строятся итерации матрицей А целого подпространства.)
Рассмотрим точный метод нахождения СЗ и СВ - метод Данилевского. В его основе лежит понятие преобразования подобия.
Метод А.М. Данилевского
В конце тридцатых годов прошлого века А.М. Данилевским был предложен метод сведения исходной матрицы 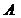 к нормальной форме Фробениуса
к нормальной форме Фробениуса 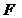 с помощью преобразований подобия вида
с помощью преобразований подобия вида 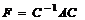 с невырожденной матрицей
с невырожденной матрицей 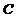 .
.
 - матрица Фробениуса или нормальная форма Фробениуса.
- матрица Фробениуса или нормальная форма Фробениуса.
Поскольку
 , то спектры матриц
, то спектры матриц 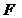 и
и 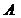 совпадают, но, как было показано выше, характеристический многочлен матрицы Фробениуса легко может быть выписан. Следовательно, задача сводится к нахождению матрицы
совпадают, но, как было показано выше, характеристический многочлен матрицы Фробениуса легко может быть выписан. Следовательно, задача сводится к нахождению матрицы 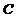 .
.
Данилевский предложил преобразовывать матрицу 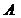 путем (
путем (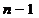 ) –го преобразования подобия, последовательно преобразуя строки матрицы
) –го преобразования подобия, последовательно преобразуя строки матрицы 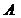 , начиная с нижних, в строки матрицы Фробениуса.
, начиная с нижних, в строки матрицы Фробениуса.
Приведем последнюю строку матрицы 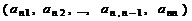 в строку вида
в строку вида 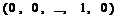 . Предположим, что разрешающий элемент
. Предположим, что разрешающий элемент 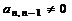 , разделим элементы (
, разделим элементы (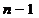 ) –го столбца матрицы
) –го столбца матрицы 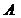 на
на 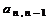 . В этом случае последняя строка примет вид
. В этом случае последняя строка примет вид  . Новый (
. Новый (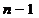 )–й столбец, умноженный соответственно на числа
)–й столбец, умноженный соответственно на числа  ,
,  ,
, 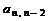 ,
, 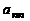 вычтем из остальных столбцов матрицы. Данные элементарные преобразования над столбцами матрицы
вычтем из остальных столбцов матрицы. Данные элементарные преобразования над столбцами матрицы 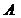 реализуются умножением справа матрицы
реализуются умножением справа матрицы 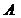 на матрицу
на матрицу  , определитель которой
, определитель которой 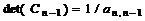 –
–
существует и отличен от нуля, при 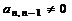 , и, следовательно, существует обратная матрица
, и, следовательно, существует обратная матрица 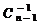 . Нетрудно проверить, что
. Нетрудно проверить, что 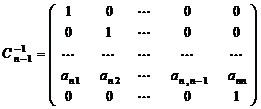 .
.
Сделаем преобразование подобия 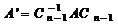 . Матрица
. Матрица  будет иметь вид:
будет иметь вид:  . На этом первый шаг преобразования заканчивается.
. На этом первый шаг преобразования заканчивается.
Второй шаг заключается в приведении предпоследней строки матрицы  к виду предпоследней строки матрицы Фробениуса и аналогичен первому шагу в предположении, что
к виду предпоследней строки матрицы Фробениуса и аналогичен первому шагу в предположении, что 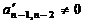 . Матрица
. Матрица  преобразуется:
преобразуется:  , где матрицы
, где матрицы  и
и 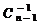 формируются аналогично. Если все разрешающие элементы отличны от нуля (так называемый регулярный случай), то за
формируются аналогично. Если все разрешающие элементы отличны от нуля (так называемый регулярный случай), то за 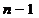 шаг данного процесса, получим форму Фробениуса:
шаг данного процесса, получим форму Фробениуса: 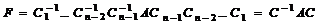 .
.
Здесь 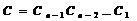 . (1)
. (1)
В нерегулярном случае: пусть сделано 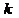 шагов преобразования, в результате которых получена матрица
шагов преобразования, в результате которых получена матрица 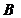 и на
и на 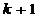 -м шаге метода, в строке с номером
-м шаге метода, в строке с номером 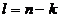 , разрешающий элемент обратился в ноль –
, разрешающий элемент обратился в ноль – 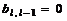 .
.

Здесь возможны два случая:
1) Левее элемента 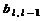 в строке найдется ненулевой элемент, например
в строке найдется ненулевой элемент, например  .
.
Переставим  -й и
-й и 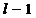 -й столбцы и, одновременно
-й столбцы и, одновременно  -ю и
-ю и 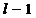 -ю строки матрицы
-ю строки матрицы 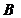 . Полученная матрица
. Полученная матрица 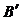 будет подобна
будет подобна 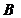 . Продолжим применение метода Данилевского для матрицы
. Продолжим применение метода Данилевского для матрицы 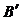 .
.
2) Все элементы 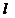 -й строки, находящиеся левее элемента
-й строки, находящиеся левее элемента 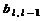 равны нулю.
равны нулю.
В этом случае имеем блочно-треугольное представление 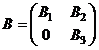 и
и  . Но матрица
. Но матрица 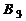 уже имеет вид Фробениуса и ее характеристический многочлен может быть выписан. Следовательно, необходимо применить метод Данилевского для матрицы
уже имеет вид Фробениуса и ее характеристический многочлен может быть выписан. Следовательно, необходимо применить метод Данилевского для матрицы  порядка
порядка  .
.
Метод позволяет найти собственные векторы матрицы 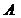 , не решая СЛАУ
, не решая СЛАУ  . Собственные векторы
. Собственные векторы  матрицы
матрицы 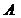 и собственные векторы
и собственные векторы 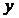 матрицы Фробениуса
матрицы Фробениуса 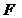 связаны соотношением
связаны соотношением
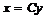 , (2)
, (2)
где 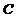 определяется формулой (1).
определяется формулой (1).
Действительно, 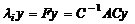 . Умножая на матрицу
. Умножая на матрицу 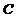 слева, получим
слева, получим 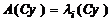 . Сравнение с формулой
. Сравнение с формулой  , дает
, дает 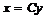 .
.
Считая, что собственные значения 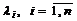 найдены, найдем собственный вектор
найдены, найдем собственный вектор 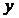 матрицы Фробениуса, соответствующий некоторому собственному значению
матрицы Фробениуса, соответствующий некоторому собственному значению  .
.
Система линейных алгебраических уравнений 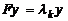 имеет вид:
имеет вид: 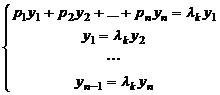 .
.
Из системы видно, что у собственного вектора формы Фробениуса все компоненты не нулевые (в противном случае вектор 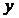 был бы нулевым, и следовательно, не мог бы быть собственным). Т.к. собственный вектор определяется с точностью до константы, то можно осуществить нормировку вектора так, чтобы его последняя компонента стала равной единице.
был бы нулевым, и следовательно, не мог бы быть собственным). Т.к. собственный вектор определяется с точностью до константы, то можно осуществить нормировку вектора так, чтобы его последняя компонента стала равной единице.
Пусть 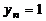 , тогда из последнего уравнения системы получим
, тогда из последнего уравнения системы получим 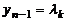 , из предпоследнего определим
, из предпоследнего определим  и т.д. Второе уравнение даст. Т.о., собственный вектор
и т.д. Второе уравнение даст. Т.о., собственный вектор 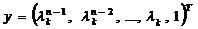 . Первое уравнение системы при этом должно тождественно выполняться. Это тождество используют для проверки правильности счета.
. Первое уравнение системы при этом должно тождественно выполняться. Это тождество используют для проверки правильности счета.