|
| Рис. 5.1. Схема включения и временные диаграммы тока и напряжения люминесцентной лампы |
|
| Рис. 5.2. Временные диаграммы напряжений и токов в нагрузке однополулериодного (а), двухполупериодного (б) и трехфазного (в) выпрямителей |
В предыдущих главах был рассмотрен расчет и анализ электрических цепей синусоидального тока. Однако на практике при генерировании, трансформации, распределении и потреблении электроэнергии возникают искажения формы синусоидальных ЭДС, напряжении и токов.
Рассмотрим основные причины возникновения периодических несинусоидальных токов и напряжений.
Несинусоидальные токи в цепях возникают при синусоидальных ЭДС и напряжениях источников электрической энергии, если цепи содержат нелинейные элементы. Так, в катушке с ферромагнитным магнитопроводом, которая является нелинейным элементом, при синусоидальном напряжении сети ток несинусоидалъный. Подобное явление наблюдается в промышленных городских сетях, когда в качестве осветительных приборов используются люминесцентные лампы, имеющие нелинейные вольт-амперные характеристики. На рис. 5.1 показана схема включения люминесцентной лампы Л в сеть синусоидального напряжения с ограничивающим дросселем L, работающим в линейном режиме, а также приведены графики тока и напряжения на лампе.
Нелинейные элементы широко используются в электрических цепях автоматики, управления, релейной защиты и т. д. Эти нелинейные элементы (стабилизаторы напряжения, умножители и делители частоты, магнитные усилители и т. п.) приводят к искажению формы кривых напряжения или тока.
Известно, что постоянный ток в энергетической электронике получают преобразованием переменного синусоидального тока с помощью выпрямителей, в которых используются нелинейные элементы — диоды (полупроводниковые, электронные и ионные). Естественно, что в таких электрических цепях возникают как несинусоидальные токи, так и несинусоидальные напряжения. На рис. 5.2 приведены временные диаграммы напряжений и токов однополупериодного, двухполупериодного и трехфазного выпрямителей, работающих на резистивную нагрузку.
|
| Рис. 5.3. Формы импульсов напряжений, используемых в импульсной технике: а — треугольного; б - прямоугольного; в — трапецеидального |
|
| Рис. 5.4. Временная диаграмма пилообразного напряжения |
В настоящее время широкое распространение получила импульсная техника, т. е. отрасль радиоэлектроники, в которой для решения определенных задач используют импульсные устройства. Режим работы подобных устройств характеризуется чередованием времени работы и пауз. Формы импульсов напряжений в импульсной технике весьма разнообразны. Основное распространение получили импульсы треугольной, прямоугольной, трапецеидальной формы и др. (рис. 5.3, а — в). В связи с этим появилось значительное разнообразие схем импульсных генераторов несинусоидальных колебаний. Такие генераторы называются релаксационными, т. е. их форма колебания выходных сигналов в значительной степени отличается от синусоиды.
Например, к релаксационным генераторам относится генератор пилообразного напряжения. Пилообразные импульсы напряжения (рис. 5.4) используются в устройствах сравнения, для горизонтальной развертки электронного луча в электронно-лучевой трубке, в радиолокационной и радиоизмерительной технике и т. д. Для формирования прямоугольных импульсов напряжения, широко применяемых в различных схемах импульсной и вычислительной техники, используются релаксационные генераторы — мультивибраторы.
Появление в электрических цепях несинусоидальных напряжений и токов может привести к весьма нежелательным последствиям. Несинусоидальные токи вызывают дополнительные потери мощности, ухудшают характеристики двигателей, создают большие помехи в линиях связи, каналах телемеханики и т. д. Заметим, что допустимое содержание гармоник оценивается коэффициентом гармоник k г (см. с. 181). Так, согласно ГОСТ 13109-67 (нормы качества электрической энергии) для промышленных сетей k г≤ 5%, т. е. в этом случае кривая напряжения на экране осциллографа визуально не отличается от синусоиды и это напряжение длительно допустимо на выводах любого приемника электрической энергии.
Разложение периодических несинусоидальных
кривых в ряд Фурье
Из математики известно, что всякая периодическая функция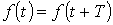 
, где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
 .
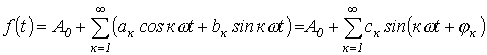| (1) |
Здесь 
- постоянная составляющая или нулевая гармоника; 
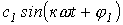- первая (основная) гармоника, изменяющаяся с угловой частотой 
, где Т – период несинусоидальной периодической функции.
В выражении (1)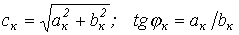 
, где коэффициенты 
и 
определяются по формулам
;
. Свойства периодических кривых, обладающих симметрией
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях.
К
ривые, симметричные относительно оси абсцисс.
К данному типу относятся кривые, удовлетворяющие равенству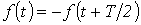 
(см. пример на рис. 2). В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е. 
.
Кривые, симметричные относительно оси ординат.
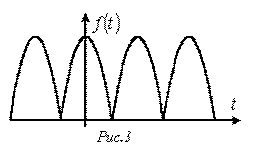
К данному типу относятся кривые, для которых выполняется равенство 
(см. пример на рис. 3). В их разложении отсутствуют синусные составляющие, т.е.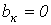 
.
К
ривые, симметричные относительно начала координат.
К этому типу относятся кривые, удовлетворяющие равенству 
(см. пример на рис. 4). При разложении таких кривых отсутствуют постоянная и косинусные составляющие, т.е. 
.