Глава1: Постановка задачи
Вариант № 13
Дано обыкновенное линейное неоднородное дифференциальное уравнение второго порядка и граничные условия:
y'' + cos(x)y' + 
y = 2x y(1) = 2 y(3) = 3
В своей работе я решаю это уравнение с помощью метода конечных разностей (далее МКР). Его суть заключается в замене дифференциальных коэффициентов уравнения на разностные коэффициенты, что позволяет свести решение дифференциального уравнения к решению его разностного аналога, то есть построить его конечно-разностную схему.
Для решения задачи необходимо задать дополнительные условия, определяющие состояния исследуемого объекта. При заданных значениях переменной эти условия называются граничными. Решение задачи делится на 4 этапа:
1) Дискретизация области изменения переменной. Интервал, ограниченный конечными условиями разбивается на n отрезков с шагом h =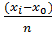 
, весь процесс называется формированием сетки с (n+1) равноудаленными узлами.
2) Производные заменяются (аппроксимируются) конечно-разностными соотношениями, в результате чего для сеточной функции, определенной в узлах сетки, получается система линейных уравнений, для замыкания которой используются граничные условия. В частности, заменяя
Приходим к системе линейных алгебраических уравнений с трехдиагональной матрицей:
3) Для решения системы используем метод прогонки, являющийся адаптацией метода Гаусса к этому случаю. Прогоночные коэффициенты вычисляются по формулам (прямая прогонка):
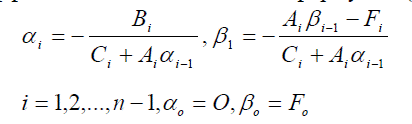
4) После прямой прогонки обратной находятся значения сеточной функции:
Глава 2: Ручной расчет
Решу данное уравнение с помощью приведенных в Главе 1 методов и формул.
y'' + cos(x)y' + y = 2x y(1) = 2 y(3) = 3
Для упрощения задачи (очевидно сложной из-за громоздких вычислений) разобью заданный интервал [1;3] на небольшое количество участков, например, n=5 частей.
| i | x | p | q | F | A | C | B | Fi |
| 1,0 | ||||||||
| 1,4 | ||||||||
| 1,8 | ||||||||
| 2,2 | ||||||||
| 2,6 | ||||||||
| 3,0 |
Построим сетку с равномерным шагом h= 
=0,4
Для систематизации вычислений составим таблицу:
Ниже приведены примеры расчета элементов таблицы
Из полученных коэффициентов составляем трехдиагональную матрицу, находим прогоночные коэффициенты и решение уравнения.
Для удобства составим еще одну таблицу
| i | A | C | B | Fi | α | β | Y | Проверка |
Глава 3: Реализация в Exсel
Глава 2 показала трудоемкость решения поставленной задачи вручную. Теперь попробуем решить то же самое уравнение
y'' + cos(x)y' + y = 2x y(1) = 2 y(3) = 3
с помощью Microsoft Office Excel. Решение состоит из использования метода конечных разностей и прямой и обратной прогонки.
Поскольку при машинном расчете количество узлов сетки не затрудняет работы, разобьем интервал на n=20 частей.
Для начала создаем на листе Excel такую же таблицу, как и в ручном расчете.
Найдем шаг 
 |
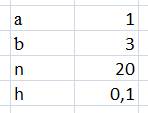
С учетом шага заполним столбец x
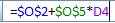
P(x)=cos(x) заполним столбец P 
Q=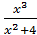 
заполним столбец q 
F=2x заполним столбец F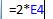 
A=1-(P(x)h)0,5 заполним столбец А 
С=2-q(x)h2 заполним столбец С 
B=1+(p(x)h)0,5 заполним столбец В 
Fi=f(x)h2 заполним последний столбец таблицы 
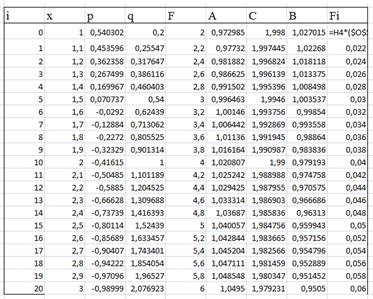
Теперь из последних четырех столбцов таблицы создаем еще одну таблицу, которая представляет матрицу, использованную в ручном расчете.
Но этого для решения явно недостаточно. Добавим столбцы α и β для коэффициентов прогонки, а также столбец Y для записи решений. Еще один столбец таблицы отведем для проверки результатов вычислений.
Получилась новая таблица:
Найдем прогоночные коэффициенты и заполним соответствующие столбцы
α0= 
αi= 
Таблица с заполненным столбцом α:
β0= - 
βi= 
Таблица с заполненным столбцом β:
Начинаем обратный ход прогонки.
Yn= βn 
yi= αi yi-1+βi 
Таблица с найденными значениями Y:
Проведем проверку полученных решений: значения столбца Проверка должны совпасть со значениями столбца Fi
F0=-C0y0+B0y1 
Fn=AnYn-1-CnYn=Fn 
Fi=AiYi-1-CiYi+BiYi+1 
Итоговый вариант таблицы с найденными значениями Y и проверкой: 
Заключение
В своей курсовой работе я решала обыкновенное линейное неоднородное дифференциальное уравнение второго порядка с заданными граничными условиями методом конечной разности:
y'' + cos(x)y' + y = 2x y(1) = 2 y(3) = 3
В качестве вспомогательного метода использовался метод прогонки.
Расчет проводился двумя способами: ручным и машинным. Для машинного расчета был использован Microsoft Office Excel 2007. Расчет в Excel, благодаря более мелкому разбиению сетки дал более точный результат. В итоге на интервале [1;3] были получены следующие корни:
-0,99242; -1,91122; -2,76298; -3,55223; -4,28146; -4,95109; -5,55946; -6,10281; -6,57517; -6,96841; -7,2721; -7,47359; -7,55799; -7,50838; -7,30604; -6,93093; -6,36236; -5,57998; -4,56508; -3,30224;-1,78135
Проверка сошлась, а, значит, найденные значения Y правильные.
Список использованной литературы:
Microsoft Excel для студента: Л. В. Рудикова — Санкт-Петербург, БХВ-Петербург, 2007 г.- 368 с.
Microsoft Office Excel 2007 (+ CD-ROM): Виктор Долженков, Александр Стученков — Москва, БХВ-Петербург, 2007 г.- 1200 с.
Исчисление конечных разностей: А. О. Гельфонд — Санкт-Петербург, КомКнига, 2006 г.- 376 с.
Лабораторные работы по информатике. САЛЕНКО С.Д., ШАТИЛОВ К.А. – Новосибирск, НГТУ, 2000г.-20 c.
Лекции и упражнения по многосеточным методам: М. А. Ольшанский — Москва, ФИЗМАТЛИТ, 2005 г.- 168 с.
Численные методы: В. Ф. Формалев, Д. Л. Ревизников — Москва, ФИЗМАТЛИТ, 2006 г.- 400 с.