При работе в Excel могут быть использованы следующие функции:
=СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
=ЧАСТОТА(массив данных; массив интервалов) – для построения вариационного ряда. Аргументами являются диапазон массива выборочных данных и столбец интервалов. Если требуется построить дискретный ряд, то здесь указываются значения варианты, если интервальный – то верхние границы интервалов («карманы»). Поскольку результатом является столбец частот, введение функции следует завершить нажатием сочетания клавиш CTRL+SHIFT+ENTER. Задавая массив интервалов при введении функции, последнее значение в нем можно и не указывать – в соответствующий «карман» будут помещены все значения, не попавшие в предыдущие «карманы». Иногда это помогает избежать ошибки, состоящей в том, что наибольшее выборочное значение не помещается автоматически в последний «карман»
Для вычисления выборочной средней используется функция =СРЗНАЧ(массив данных). Для вычисления средней в интервальном ряду нужно перейти к дискретному ряду, заменив интервал его средним значением.
Для нахождения моды и медианы по выборке в Excel используются соответственно функции =МОДА(массив данных) и =МЕДИАНА(массив данных).
Наиболее простой характеристикой вариации признака является размах вариации: R=x max –x min,
где x max – наибольшее, x min – наименьшее значения в выборке.
Размах вычисляется при помощи формулы: =МАКС(массив данных)-МИН(массив данных)
Дисперсия Dв выборки вычисляется при помощи функции =ДИСПР(массив данных).
Исправленная дисперсия s2 выборки вычисляется с помощью =ДИСП(массив данных).
Корень квадратный из дисперсии представляет среднее квадратическое отклонение или стандартное отклонение и вычисляется с помощью команды =КОРЕНЬ(номер ячейки) или =СТАНДОТКЛОНП(массив данных).
Корень квадратный из исправленной дисперсии представляет исправленное среднее квадратическое отклонение или стандартное отклонение и вычисляется с помощью команды =КОРЕНЬ(номер ячейки) или =СТАНДОТКЛОН(массив данных).
Коэффициент асимметрии и эксцесс по выборке вычисляются функциями: =СКОС(массив данных) и =ЭКСЦЕСС(массив данных).
Для вычисления основных выборочных характеристик в Excel можно использовать также процедуру «Описательная статистика» из надстройки «Пакет анализа».
Чтобы изменить (уменьшить) количество знаков после запятой в полученных значениях для выборочной средней, дисперсии,… надо выделить нужные ячейки, нажать правую кнопку мыши, выбрать «формат ячеек», «числовой» и поставить нужное число знаков после запятой.
Критическая точка c2(a; n-1) распределения хи-квадрат Пирсона находится с помощью функции функция =ХИ2ОБР(a; n-1) при уровне значимости a=(1-β)/2 и n-1 степени свободы.
В Excel критическая точка распределения Стьюдента (для малой выборки) с уровнем значимости 2a=1-β рассчитывается с помощью =СТЬЮДРАСПОБР(вероятность; степени свободы), где за аргумент вероятность принимается уровень значимости 2a=1-β. Для нахождения доверительного интервала для мат. ожидания при неизвестной дисперсии используется n-1 степень свободы.
Доверительный интервал для дисперсии s2 вычисляется по формуле
(n-1)*s2 / c2(a; n-1) < s2 < (n-1)*s2 / c2(1-a; n-1), (*)
где значение c2(a; n-1) находится с помощью функции функция =ХИ2ОБР(a; n-1) при уровне значимости a и n-1 степени свободы. Для нахождения доверительного интервала для среднего квадратического отклонения s извлекаются корни квадратные из концов интервала (*).
В Excel критическое значение критерия Фишера можно рассчитать при помощи функции FРАСПОБР(вероятность;степени_свободы1;степени_свободы2), где вероятность – уровень значимости a=(1-β)/2.
Пример 1
Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Решение. Откроем таблицы Excel. Введем массив данных в диапазон А1:L5. Если Вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон. Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:J5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить. Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:J5), и в ячейку В9: =МАКС(А1:J5).
Поскольку требуется интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу
=1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
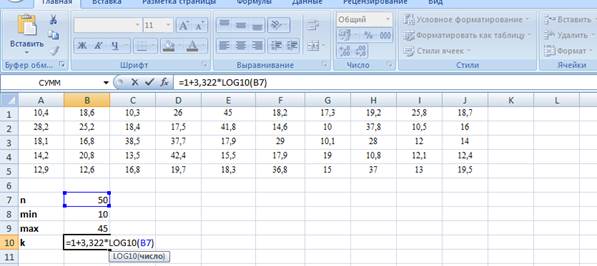
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(B9-B8)/C10.
Зададим массив интервалов, указывая для каждого из 7 интервалов верхнюю границу. Для этого в ячейке Е8 вычислим верхнюю границу первого интервала, введя формулу =B8+B11; в ячейке E9 верхнюю границу второго интервала, введя формулу =E8+B11. Для вычисления оставшихся значений верхних границ интервалов зафиксируем номер ячейки В11 в введенной формуле при помощи знака $, так что формула в ячейке Е9 примет вид =E8+B$11, и скопируем содержимое ячейки E9 в ячейки E10-E14, «потянув» за правый нижний уголок ячейки. Последнее полученное значение равно вычисленному ранее в ячейке B9 максимальному значению в выборке.
Рис.1.5. Пример 2. Построение равноинтервального ряда

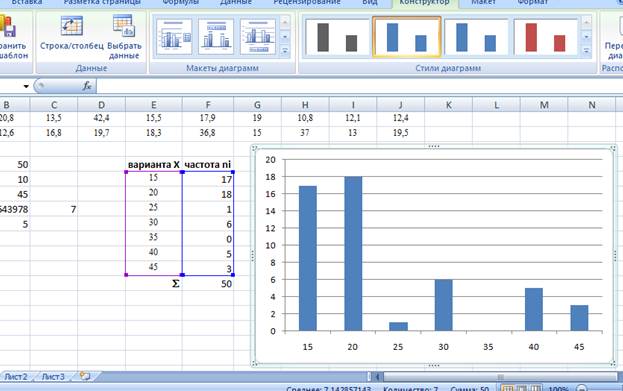
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:J5;E8:E14) и нажмем сочетание клавиш CTRL+SHIFT+ENTER.
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Рис.1.6. Пример 2. Построение равноинтервального ряда

По полученному вариационном ряду построим гистограмму: выделим столбец частот и выберем на вкладке «Вставка» «Гистограмма». Получив гистограмму, изменим в ней подписи горизонтальной оси на значения в диапазоне интервалов, для этого выберем опцию «Выбрать данные» вкладки «Конструктор». В появившемся окне выберем команду «Изменить» для раздела «Подписи горизонтальной оси» и введем диапазон значений варианты, выделив его «мышью».
Рис.1.7. Пример 2. Построение гистограммы

Рис.1.8. Пример 2. Построение гистограммы