РАСЧЕТ ОДНОКОНТУРНОЙ СИСТЕМЫ РЕГУЛИРОВАНИЯ

Задание:

Динамические свойства объекта регулирования по каналу регулирующего воздействия определены импульсной характеристикой.

Регулируемая величина — температура перегретого пара котельного агрегата. Импульсная характеристика получена в результате нанесения возмущения, созданного скачкообразным уменьшением и последующим скачкообразным увеличением через подачи конденсата на впрыск в пароохладитель на величину , измеренную в процентах хода регулирующего органа (% ). Максимальный расход конденсата на впрыск, соответствующий 100% , составляет 6 т/час. Номинальная температура перегретого пара 400⁰ С. Изменение регулируемой величины (в отклонениях от номинального значения) в результате импульсного возмущающего воздействия, задано в безразмерном виде таблицей 1.

Таблица 1

 

 

1. Получение импульсной кривой

Исходные данные:

Тип задания №1

ПИД-регулятор

t_имп= 60 секунд;

x_{вх. имп} = 10% х.р.о.

a_t = 10 секунд

a_θ = 2 градусов

М = 1,55

x_вх 100% х.р.о. = 6 тонн/час

t_пара= 400

Так как изменение регулируемой величины задано в безразмерном виде, нужно получить импульсную характеристику в размерном виде:

t = · a_t; θ= ·а_θ, получим:

Импульсная характеристика:

t, сек

θ, град

 

Построим график импульсной характеристики:

Определим динамические параметрыобъекта (k, T, τ) по импульсной характеристике:

 

 

σ_макс=30

τ=35 с

Импульсный входной сигнал:

 

=60 ∙ 10=600

 

Постоянная времени:

 

Коэффициент усиления:

 

– максимальное отклонение регулируемой величины;

– площадь, описываемая кривой изменения возмущения;

– площадь, описываемая кривой изменения регулируемой величины.

 

Смоделируем процесс в Matlab:

 

2. Перестроение импульсной кривой в кривую разгона и определение параметров объекта

Для перестройки импульсной характеристики в кривую разгона h(t) разбиваем наблюдаемое время на интервалы и складывая ординаты графиков и h(t) по формуле h(t) = h(t)_i-1 + (t)_i, предварительно интерполируя импульсную характеристику _i.

Перестроим импульсную кривую в кривую разгона и определим параметры объекта при t_имп=60 с, по правилу:

 

;

T ≤ t ≤ 2T

 

t, сек
h, град

 

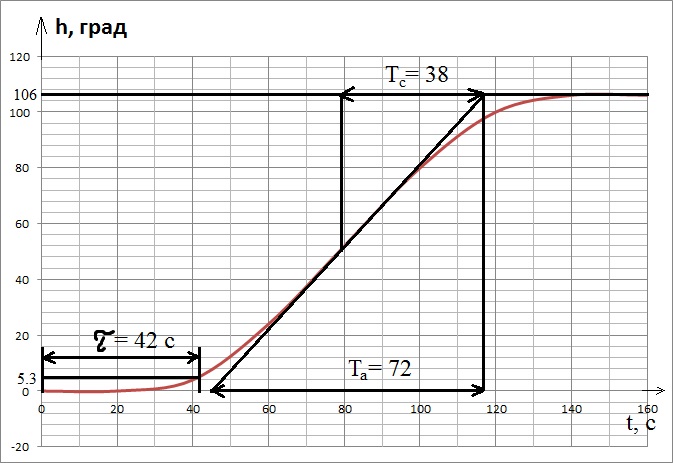
Отыщем точку перегиба методом Ольденбурга-Сарториуса

Для упрощения задачи идентификации модели определим предварительно время запаздывания путем графического решения уравнения

 

y(τ)=Δ=0.05y(Тп)

 

Время запаздывания τ= 42с

Рассчитаем параметры k, τ, T_c,T_a, T_1,T ₂

Коэффициент усиления регулируемого объекта находим как отношение установившегося значения выхода к значению входа:

 

К =106/10 = 10,6

 

Находим точку перегиба графика переходной функции и определяем величины

 

Ta=72, Tc=38, Tc/Ta=0,53.

С помощью диаграммы Ольденбурга–Сарториусапо известной величине Tc/Ta находим постоянные времени:

 

T₁/T_a =0,37

T₂/T_a =0,37

Т₁ = 0,37 ∙ T_a=26,64

Т₂ =0,37 ∙ T_a=26,64

а₁* = Т₁+Т₂=53,28

а₂* =Т₁∙ Т₂ =709,69

 

Идентифицированная модель динамики:

 

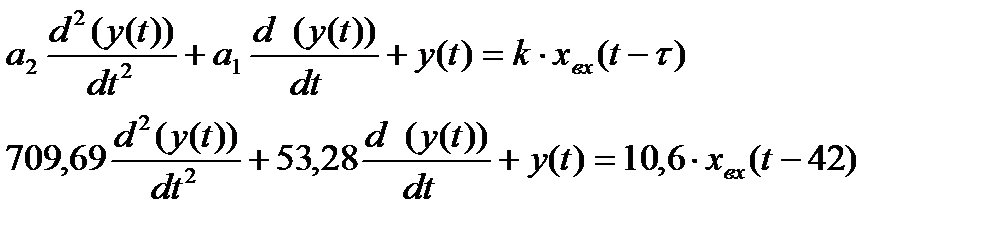
Получили передаточную функцию в дифференциальном виде.

Получим передаточную функцию:

 

 

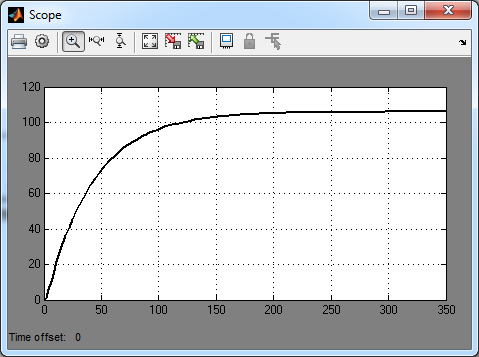
Смоделируем процесс в Matlab:

 

 

Получили кривую разгона:

 

 

3. Определение по кривой разгона «методом площадей» передаточной функции регулируемого объекта , при помощи программы simou.exe

 

Модель №1

W(s) =

 

Исходные данные для расчета:

Параметры передаточной функции:

Коэффициент усиления K = 10.6

Запаздывание tau = 0

Коэффициенты числителя (степень m = 0):

b[0] = 1

Коэффициенты знаменателя (степень n = 1):

a[0] = 1 a[1] = 41.13208

Величина входного сигнала х = 10

Модель №2

W(s)=

 

Исходные данные для расчета:

Параметры передаточной функции:

Коэффициент усиления K = 10.6

Запаздывание tau = 0

Коэффициенты числителя (степень m = 0):

b[0] = 1

Коэффициенты знаменателя (степень n = 2):

a[0] = 1.00000 a[1] = 41.13208 a[2] = 554.74071

Величина входного сигнала х = 10

Модель №3

W(s)=

 

Исходные данные для расчета:

Пареметры передаточной функции:

Коэффициент усиления K = 10.6

Запаздывание tau = 0

Коэффициенты числителя (степень m = 0):

b[0] = 1

Коэффициенты знаменателя (степень n = 2):

a[0] = 1.00000 a[1] = 41.13208 a[2] = 554.74071 a[3] = -205.50298

Величина входного сигнала х = 10

 

4. Построим и сравним полученные переходные характеристики передаточных функций с помощью пакета Simulink.

Сравниваем полученные переходные характеристики передаточных функций:

5. Представление динамической модели объекта соединением типовых динамических звеньев, смоделировать объект на базе имитационного моде­лирования (Simulink), получить кривые разгона и сравнить их с рассчитан­ной.

Кривая, полученная методом Ольденбурга-Сарториуса:

 

W(p)₁ =

 

Кривая, полученная методом интегральных площадей (Симою):

 

W(p)₂ =

 

 

Кривая, полученная методом интегральных площадей (Симою):

 

W(p)₃ =

 

Кривая, полученная методом интегральных площадей(Симою):

 

W(p)₄ = =

 

 

6. Частотные характеристики объекта регулирования (АФХ, АЧХ и ФЧХ):

 

W(p)=

 

Расчет частотныххарактеристик.

Исходные данные для расчета

Параметры передаточной функции:

Коэффициент усиления	K = 10,6
Запаздывание	tau = 40
Коэффициенты числителя	b[0] = 1
Коэффициенты знаменателя	a[0] = 1 a[1] = 41,13 a[2] =554,74

Вид передаточной функции:

 

W(p)=

 

Параметры расчета:
Расчет нормальных частотных характеристик.

Количество точек	N = 11
Начальная частота	w0 = 0
Шаг по частоте	dw = 0,02

Результаты расчета:

Частотные характеристики.

 

АФХ – амплитудно-фазовая характеристика

АЧХ - амплитудно-частотная характеристика

 

ФЧХ – фазо-частотная характеристика

 

Частота ReImA(w) fi(w)

0.02000 -0.39674 -9.35302 9.36143 267.57109

0.03000 -5.79003 -5.46256 7.96016 223.33307

0.04000 -6.42310 -0.25076 6.42800 182.23568

0.05000 -4.13699 2.92319 5.06554 144.75498

0.06000 -1.39407 3.73059 3.98255 110.48997

0.07000 0.61714 3.10068 3.16150 78.74337

0.08000 1.67466 1.91800 2.54621 48.87482

0.09000 1.95205 0.72571 2.08258 20.39351

0.10000 1.71568 -0.21232 1.72877 -7.05463

0.11000 1.20990 -0.80756 1.45465 -33.72149

0.12000 0.62347 -1.07068 1.23898 -59.78730

7. Для заданного регулятора заданным методом рассчитаем оптимальные значения параметров настройки, обеспечивающих заданный запас устойчивости системы. Расчет параметров ведется по расширенным частотным характеристикам.

Передаточная функция объекта управления имеет вид:

 

W_о(p)=

 

Передаточная функция регулятора:

 

Необходимо подобрать оптимальные значения параметров настройки (С1, С0), чтобы они обеспечивали заданный запас устойчивости системы.

Необходимо произвести подстановку в характеристическое уравнение замкнутой системы и выделить действительную и мнимую части полинома.

Найдемm:

 

 

Из двух корней m₁ и m₂ выбираем меньший. То есть принимаем m=0,345.

 

W_о(m,jω)=

 

ПИД-регулятор:

 

С₀=ω(m²+1)·(Im· (ω) + ω·C₂);

C₁=m·Im·(ω) –Re·(ω) + 2m·ω·C₂.

 

Примем С₂=0,1.

 

Строим график, отображающий зависимость C₀(С₁):

Строим зависимость 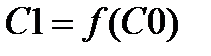и определяем и следующим образом: находим на кривой точку максимума, выбираем точку правее нее.

Схема полученной системы регулирования:

 

Значение настройки регулятораС1	Значение настройки регулятора С0	Интегральный критерий качества I
0,045	0,00144
0,050	0,001428
0,055	0,001378
0,060	0,001268
0,065	0,000919

 

Примем С₂=0,5.

 

 

Строим график, отображающий зависимость C₀(С₁):

Построим зависимость 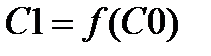и определим и следующим образом: находим на кривой точку максимума, выбираем точку правее нее.

Схема полученной системы регулирования:

 

Значение настройки регулятораС1	Значение настройки регулятора С0	Интегральный критерий качества I
0,07	0,001686
0,075	0,001675
0,08	0,001637
0,085	0,001557
0,09	0,001349
0,092	0,001124

Примем С₂=1,2.

 

 

Строим график, отображающий зависимость C₀(С₁):

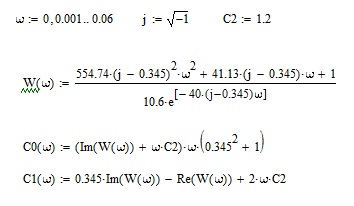
Строим зависимость 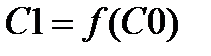и определяем и следующим образом: находим на кривой точку максимума, выбираем точку правеенее.

Схема полученной системы регулирования:

 

Значение настройки регулятораС1	Значение настройки регулятора С0	Интегральный критерий качества I
0,12	0,002199
0,125	0,002187
0,13	0,002153
0,135	0,002069
0,14	0,001931

 

С0	С1	С2	I
0,06	0,001268	0,1
0,09	0,001349	0,5
0,125	0,002187	1,2

 

Из таблицы видно, что наилучшими свойствами будет обладать ПИД-регулятор с настройками: С₀=0,09, С₁=0,001349 и С₂=0,5 при рабочей частоте ω=0,031 рад/с.

График переходного процесса полученной системы регулирования:

 

8. Составим структурную схему системы регулирования (при найденных оптимальных настройках регулятора). Получим передаточную функцию замкнутой системы относительно внешнего возмущающего воздействия.

В качестве передаточной функции объекта относительно возмущающего воз­действия возьмем передаточную функцию , определенную в п.1.

 

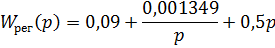
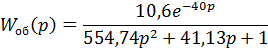
Передаточная функция замкнутой сис­темы по возмущающему воздействию:

 

9. Расчет и построение КЧХ замкнутой системы относительно возму­щающего воздействия.

 

 

Делаем подстановку p = 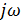, выделяем действительную и мнимую часть:

 

КЧХ замкнутой системы относительно возму­щающего воздействия:

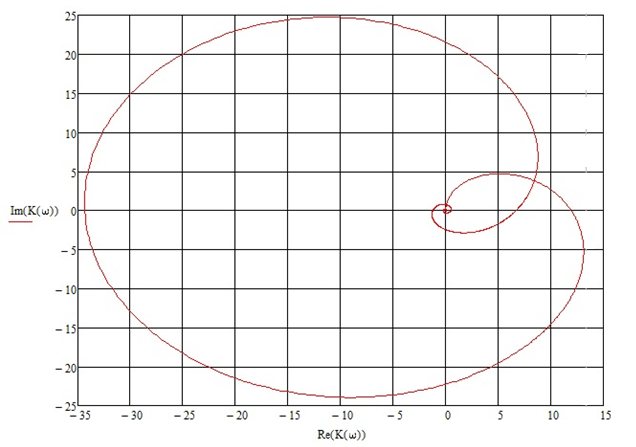
10.Смоделируем систему на базе имитационного моделирования в программе Simulink, получим переходный процесс при заданном возмущающем воздействии:

 

График переходного процесса:

11. Оценка качества переходного процесса по возмущению.

1) Время регулирования: t_р= 385 с;

2) Перерегулирование:

 

σ = |y_max­1 – y_уст| = 22,7;

 

3) Время достижения первого максимума: t_max=78,5;

4) Квадратичный интегральный критерий качества:

 

 

 

5) Частота переходного процесса:

 

 

6) Время затухания за 1 период:

 

 

7) Степень затухания:

 

 

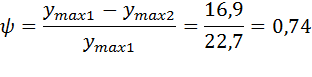
8) Степень колебательности:

 

 

ВЫВОД

В данном курсовом проекте я:

- определил по кривой разгона «методом площадей» передаточную функцию регулируемого объекта;

- рассчитал и построил частотные характеристики объекта регулирования (КЧХ, АЧХ и ФЧХ). Для ПИД-регулятора методом расширенных частотных характеристик рассчитал оптимальные значения параметров настройки, обеспечивающие заданный запас устойчивости системы, и минимальное значение квадратичного интегрального критерия качества;

- получил переходный процесс, являющийся оптимальным, оценил качество полученного переходного процесса: время регулирования = 385 с.; перерегулирование = 22,7; коэффициенты затухания = 0,26 и колебательности = 0,21;

- рассчитал и построил КЧХ замкнутой системы относительно возмущающего воздействия;

- построил переходный процесс в системе регулирования при единичном скачкообразном возмущающем воздействии;

Построенная мной система АСР объектом управления, взятая на основе реального объекта управления является устойчивой, т.к. в системе возможен установившийся режим. Параметры удовлетворяют необходимым условиям регулируемого объекта и вполне приемлемы для его нормального функционирования, вследствие чего регулируемый параметр, т.е. температура перегретого пара в котле будет поддерживаться на необходимом уровне.

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1. Востриков, А.С. Теория автоматического регулирования: Учеб.пособие/ Востриков А.С., Французова Г.А.– Новосибирск: Изд-во НГТУ, 2003.– 364 с.

2. Ротач,В.Я.Теория автоматического управления теплоэнергетическими процессами:

Учебник для вузов / Ротач В.Я.–М: Энергоатомиздат, 1985.– 296 с.

3. Клюев, А.С.Наладка средств автоматизации и автоматических систем регулирования: Справочное пособие / КлюевА.С.,

ЛебедевА.Т. – М.: Энергоатомиздат,1989.

4. Прохватилов В.В.Методические указания к выполнению курсового проекта по теории автоматического управления: Методические указания / Прохватилов В.В.,

Кантемиров В.И.– Астрахань: Изд-во АГТУ, 2007.– 35 с.

5. Стефани Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов / Стефани Е.П..– М: Энергия, 1972.– 376 с.