Доклад
по предмету:
«Математический анализ»
по теме:
«Знакопостоянные числовые ряды»
Выполнила: студентка
Группы 98АТП-П
Карпова М.А.
Содержание:
1. Основные определения. 3
2. Свойства сходящихся рядов. 6
3. Необходимое условие сходимости ряда (критерий Коши). 8
4. Достаточные условия сходимости рядов. 9
Признак сравнения 1. 9
Признак сравнения 2. 9
Признак Даламбера. 10
Признак Коши. 12
Интегральный признак Коши. 13
Список используемой литературы: 14
Основные определения.
Пусть дна числовая последовательность a1, a2, …, an, … Выражение вида
(1)
называется числовым рядом.
Числа a1, a2, …, an … называются членами ряда, а член an с произвольным номером - общим членом ряда.
Суммы конечного числа членов ряда
называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм
S1, S2, S3, …, Sn, … (2)
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое в этом случае называется суммой ряда (1). Символически это записывается так:
или 
.
Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящим.
Пример 1: Покажем, что ряд
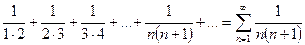
сходится. Возьмем сумму 
первых n членов ряда 
Слагаемые этой суммы могут быть представлены в виде
.
Поэтому
.
Отсюда следует, что предел последовательности частичных сумм данного ряда равен единице: 
. Таки образом, ряд сходится, и его сумма S равна 1.
Пример 2: Установим, сходится или расходится ряд
.
Последовательность его частичных сумм имеет вид S1=1, S2=0, S3=1, S4=0, … и, значит, не сходится ни к какому пределу, поэтому данный ряд расходится.
|
|
Пример 3: Рассмотрим ряд, составленный из элементов геометрической прогрессии 
, 
(3)
Частичная сумма Sn этого ряда при 
имеет вид
.
Отсюда:
1) Если 
то 
, т.е. ряд сходится и его сумма 
. Например, при 
имеем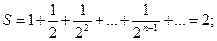 
2) Если 
то 
, т.е. ряд расходится;
3) При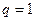 
ряд (3) принимает вид 
В этом случае 
, т.е. ряд расходится;
4) При 
ряд (3) принимает вид 
Для него 
т.е.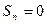 
при n четном и 
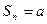при n нечетном. Следовательно, 
не существует и ряд расходится.
Таким образом, ряд (3) является сходящимся при 
и расходящимся при 
.
Свойства сходящихся рядов.
Теорема 1: Если сходится ряд
, (4)
то сходится и ряд 
, (5)
и обратно, если сходится ряд (5), то сходится и ряд (4).
Доказательство. Пусть ряд (4) сходится и имеет сумму S, т.е.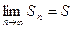 
. Обозначим через 
сумму отброшенных членов ряда (4), а через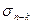 
сумму n-k первых членов ряда (5). Тогда
, (6)
где - некоторое число, не зависящее от n. Из равенства (6) следует 
, т.е. последовательность частичных сумм 
ряда (5) имеет предел, что означает сходимость ряда (5).
Пусть теперь ряд (5) сходится и имеет сумму 
, т.е.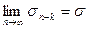 
. Тогда из (6) следует 
, что означает сходимость ряда (4).
Теорема 2: Если ряд 
сходится и его сумма равна S, то и ряд 
, где с – некоторое число, также сходится, и его сумма равна cS.
Доказательство. Пусть - частичная сумма ряда , а 
- частичная сумма ряда . Тогда
.
Отсюда, переходя к пределу при 
, получаем 
, т.е. последовательность частичных сумм 
ряда сходится к cS. Следовательно,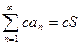 
.
Теорема 3: Если ряд и 
сходятся и их суммы соответственно равны S и , то и ряд 
сходится и его сумма равна 
.
Доказательство. Пусть и - частичные суммы рядов и , а 
- частичная сумма ряда . Тогда
|
|
Отсюда, переходя к пределу при , получаем 
, т.е. последовательность частичных сумм 
ряда сходится к . Следовательно 