Порядок выполнения округления

ПРАКТИЧЕСКАЯ РАБОТА №1.

Оценка погрешности экспериментального определения
физической величины.

Основные положения.

Наилучшей оценкой истинного значения величины является выборочное среднее значение

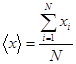, (1.1)

где – отсчёт величины ; – число отсчётов.

Для оценки разброса отсчётов при измерении используется выборочное среднее квадратическое отклонение отсчётов

. (1.2)

Выборочное среднее является случайной величиной и его разброс относительно истинного значения измеряемой величины оценивается выборочным средним квадратическим отклонением среднего значения

. (1.3)

Доверительным интервалом называется интервал , который с заданной степенью достоверности включает в себя истинное значение измеряемой величины.

Случайную составляющую погрешности принято выражать как полуширину доверительного интервала. Размер доверительного интервала обычно задают в виде кратного значения. Случайная составляющая погрешности многократных измерений определяется как:

, (1.4)

где 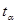– безразмерный коэффициент доверия (коэффициент Стьюдента).

Коэффициент 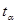показывает, во сколько раз нужно увеличить , чтобы при заданном числе измерений получить заданную надёжность результата. Коэффициент 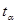определяют по статистическим таблицам (табл. 1).

Полная погрешность измерений равна квадратичной сумме инструментальной и случайной погрешностей.

Таблица 1.

Значения коэффициента Стьюдента в зависимости от числа измерений

Число измерений	Надежность
0,5	0,9	0,95	0,98	0,99	0,999
		6,3	12,7	31,8	63,7	636,7
	0,82	2,9	4,3	7,0	9,9	31,6
	0,77	2,4	3,2	4,5	5,8	12,9
	0,74	2,1	2,8	3,7	4,6	8,6
	0,73	2,0	2,6	3,4	4,0	6,9
	0,72	1,9	2,4	3,1	3,7	6,0
	0,71	1,9	2,4	3,0	3,5	5,4
	0,71	1,9	2,3	2,9	3,4	5,0
	0,70	1,8	2,3	2,8	3,2	4,8
	0,69	1,7	2,1	2,5	2,8	3,8
>20	0,67	1,6	2,0	2,5	2,8	3,3

 

Обработку прямых измерений рекомендуется начинать с проверки отсчётов на наличие промахов. Из полученного ряда, содержащего отсчётов, выбирается аномальный (минимальный или максимальный наибольее отличающийся от среднего) отсчёт и вычисляется модуль его отклонения от среднего значения в долях выборочного среднего квадратического отклонения:

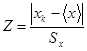. (1.5)

Далее оценку производят по критерию Шовене (табл. 2). В случае, если ожидаемое число отсчетов среди которых будет хотя бы один аномальный будет больше числа проведенных отсчетов , то считается промахом.

Таблица 2.

Отбор промахов по критерию Шовене

Z	M	Z	M	Z	M	Z	M	Z	M
1,00		1,40		1,80		2,20		2,60
1,02		1,42		1,82		2,22		2,62
1,04		1,44		1,84		2,24		2,64
1,06		1,46		1,86		2,26		2,66
1,08		1,48		1,88		2,28		2,68
1,1		1,50		1,90		2,30		2,70
1,12		1,52		1,92		2,32		2,72
1,14		1,54		1,94		2,34		2,74
1,16		1,56		1,96		2,36		2,76
1,18		1,58		1,98		2,38		2,78
1,20		1,60		2,00		2,40		2,80
1,22		1,62		2,02		2,42		2,82
1,24		1,64		2,04		2,44		2,84
1,26		1,66		2,06		2,46		2,86
1,28		1,68		2,08		2,48		2,88
1,30		1,70		2,10		2,50		2,90
1,32		1,72		2,12		2,52		2,92
1,34		1,74		2,14		2,54		2,94
1,36		1,76		2,16		2,56		2,96
1,38		1,78		2,18		2,58		2,98

 

Алгоритм обработки прямых измерений:

1. Определить инструментальную погрешность.

2. Вычислить среднее значение серии измерений по формуле (1.1).

3. Вычислить среднее квадратическое отклонение отсчёта по формуле (1.2). Если промах устранён, то перейти к формуле (1.4), иначе к (1.3).

4. Проверить отсчёты на наличие промаха:

• отобрать аномальный отсчёт;

• вычислить его относительное отклонение по формуле (1.5);

• определить ожидаемое число отсчётов, среди которых может быть аномальный, если это число больше числа отсчётов, то исключить аномальный отсчёт и перейти к формуле (1.1); иначе перейти к (1.4).

5. Вычислить выборочное среднее квадратическое отклонение среднего значения по формуле (1.3).

6. Определить коэффициент доверия для заданной надёжности и полученного числа отсчётов.

7. Вычислить случайную погрешность по формуле (1.4).

8. Вычислить полную погрешность.

9. После округлений результат обработки измерений записать в форме: ед. измерения; ; .

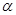Порядок выполнения округления

Выполнить предварительную запись окончательного результата измерения в виде и вынести за общую скобку одинаковые порядки среднего и погрешности, т.е. множитель вида 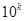, где k – целое число. Числа в скобках переписать в десятичном виде с использованием запятой, убрав тем самым оставшиеся порядковые множители.

Округлить в скобках число, соответствующее погрешности, до одной значащей (ненулевой) цифры слева, если эта цифра больше 2, или до двух первых цифр в противном случае. При округлении используют правило: если цифра, расположенная за оставляемой, меньше 5, то ее просто отбрасывают, иначе оставляемую цифру увеличивают на единицу. Если же отбрасываемая цифра равна 5, то наименьшая ошибка достигается при округлении по правилу Гаусса до ближайшего четного числа. К примеру, 4,5 округляют до 4, в то время как 3,5 также округляют до 4.

Округлить в скобках число, соответствующее среднему значению: последними справа оставляют цифры тех разрядов, которые сохранились в погрешности после ее округления.

Окончательно записать с учетом выполненных округлений. Общий порядок и единицы измерения величины приводят за скобками – получена стандартная форма записи.

 

Пример. Вольтметром измерено 10 отсчётов напряжения в электрической цепи. Вольтметр, класс точности которого 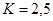, имеет максимальное значение шкалы, равное 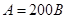. Результаты измерений представлены в табл. 3. Необходимо обработать результаты измерений, обеспечив 98 % надёжность оценки напряжения.

Таблица 3.

Результаты измерения напряжения

№
, В

Вычисляем инструментальную погрешность В.

Для заданной доверительной вероятности и количества отсчётов определяем коэффициент доверия (см. табл. 1).

Вычисляем среднее значение В. Вычисляем среднее квадратическое отклонение отсчётов В.

Проверяем отсчёты на наличие промахов. Аномальным отсчётом является отсчёт № 4. Вычисляем нормированное отклонение от среднего . Согласно табл. 2, количество опытов, при котором полученный отсчёт нельзя считать промахом, равно 17. Это число больше, чем N = 10. Следовательно, отсчёт № 4 является промахом и его нужно удалить из обрабатываемого ряда. Для нового ряда отсчётов напряжения вычисляем новое среднее значение и среднее квадратическое отклонение. Вычисляем случайную составляющую погрешности В, В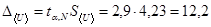. Вычисляем полную погрешность: абсолютную (округление погрешности производят до одной значащей цифры слева, если она больше 2; в нашем случае 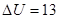) и относительную .

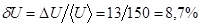После округлений результат измерения напряжения записываем в виде:
, , .

 

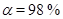Индивидуальное задание.

 

Прибором измерено 10 отсчётов физической величины. Класс точности прибора K = 2,5, максимальное значение шкалы A = 200 В. Результаты измерений представлены в табл. 4. Необходимо обработать результаты измерений, обеспечив 98 % надёжность оценки напряжения.

Таблица 4.

Результаты измерения физической величины

Вариант	№ измерения